sklearn基本用法

---

加载数据(Data Loading)

数据集：pima-indians.data.csv

“皮马印第安人糖尿病问题”作为测试数据集。其中包括768个患者的记录数据，每条记录的第一列为记录序号，后面跟着每条记录的7个数值型数据特征，最后第9列是0/1标签值，表示患者是否是在5年之内感染的糖尿病。

#coding=utf-8
#加载数据
import numpy as np
import urllib

# url with dataset
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/pima-indians-diabetes/pima-indians-diabetes.data"

# download the file
raw_data = urllib.urlopen(url)

# load the CSV file as a numpy matrix
dataset = np.loadtxt(raw_data, delimiter=",")

# separate the data from the target attributes
X = dataset[:,0:7]            #特征矩阵为X
y = dataset[:,8]              #标签为y

数据归一化(Data Normalization)

进行归一化或标准化

1. 归一化：通过对原始数据进行线性变换把数据映射到[0,1]之间。

   原理：不同变量往往量纲不同，归一化可以消除量纲对最终结果的影响，使不同变量具有可比性。

   其中min是样本中最小值，max是样本中最大值，在数据流场景下最大值与最小值是变化的。而且最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。公式：
   

2. 标准化：去除均值和方差的缩放，将数据按特征减去其均值后除以其方差。使得对于每个特征来说所有数据都聚集在0附近，方差为1。

   原理：公式表示的是原始值与均值之间差多少个标准差，是一个相对值，所以也有去除量纲的作用。同时还使得均值为0，标准差为1。因为每个变量的重要程度正比于这个变量在这个数据集上的方差。如果让每一维变量的标准差都为1（即方差都为1），则每维变量在计算距离的时候重要程度相同。

   其中μ是样本的均值，σ是样本的标准差，可以通过现有样本进行估计。在已有样本足够多的情况下比较稳定，适合嘈杂大数据场景。公式：
   

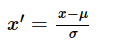
#数据归一化
from sklearn import preprocessing

# normalize the data attributes
normalized_X = preprocessing.normalize(X)

# standardize the data attributes
standardized_X = preprocessing.scale(X) #直接将给定数据进行标准化

#scaler = preprocessing.StandardScaler().fit(X)  另一种方式，用sklearn.preprocessing.StandardScaler类标准化，可以保存训练集中的参数（均值、方差）直接使用根据训练集生成的scaler对象转换测试集数据，使训练集生成的参数作用于测试集。

使用场景：在涉及到计算点与点之间的距离时，归一化或标准化都会对最后的结果有所提升。如果所有维度的变量在最后计算距离中发挥相同的作用，则应该选择标准化；如果想保留原始数据中由标准差所反映的潜在权重关系，应该选择归一化。

特征选择(Feature Selection)

解决实际问题时，选择合适的特征或重新抽象、构建特征非常重要。已经有许多现成的算法用于特征选择。下面的例子用ExtraTreesClassifier计算特征的信息量：

from sklearn.ensemble import ExtraTreesClassifier

model = ExtraTreesClassifier()
model.fit(X,y)

# display the relative importance of each attribute
print(model.feature_importances_)

每个特征的重要程度用浮点值表示出来，根据运行结果可知第二维特征的区分能力最强。

分类器属于Extremely Randomized Trees算法，它包含两个类，分类用 ExtraTreesClassifier 回归用ExtraTreesRegressor。

基本算法

逻辑回归

from sklearn import metrics
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X, y)
print(model)

# make predictions
expected = y
predicted = model.predict(X)

# summarize the fit of the model
print(metrics.classification_report(expected, predicted))

print(metrics.confusion_matrix(expected, predicted))        #计算混淆矩阵以评估分类的准确性

混淆矩阵：

分类常用的评价指标有：混淆矩阵、分类准确率、召回率、f1-score等。sklearn.metrics 模块覆盖了其中大部分指标。

混淆矩阵（confusion matrix）是可视化工具，对分类模型进行性能评价的重要工具。特别用于监督学习，在无监督学习一般叫做匹配矩阵。其每一列代表预测值，每一行代表样本的实际类别，所有正确的预测结果都在对角线上。结构：

朴素贝叶斯

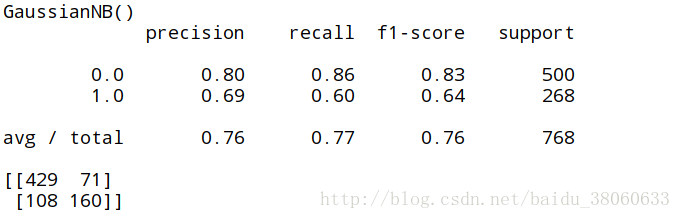
用于还原训练样本数据的分布密度，在多类别分类中有很好的效果。

from sklearn import metrics
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X, y)
print(model)

# make predictions
expected = y
predicted = model.predict(X)

# summarize the fit of the model
print(metrics.classification_report(expected, predicted))
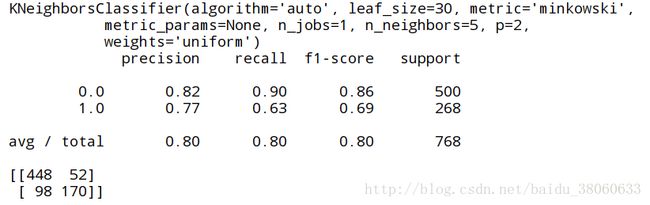
print(metrics.confusion_matrix(expected, predicted))

KNN

常被用作分类算法一部分，可用来评估特征、特征选择。

from sklearn import metrics
from sklearn.neighbors import KNeighborsClassifier

# fit a k-nearest neighbor model to the data
model = KNeighborsClassifier()
model.fit(X, y)
print(model)

# make predictions
expected = y
predicted = model.predict(X)

# summarize the fit of the model
print(metrics.classification_report(expected, predicted))
print(metrics.confusion_matrix(expected, predicted))

决策树

决策树有两种类型，分别用于分类和回归(Classification and Regression Trees ,CART)。常用于特征含有类别信息的分类或者回归问题，适用于多分类。

from sklearn import metrics
from sklearn.tree import DecisionTreeClassifier

# fit a CART model to the data
model = DecisionTreeClassifier()
model.fit(X, y)
print(model)

# make predictions
expected = y
predicted = model.predict(X)

# summarize the fit of the model
print(metrics.classification_report(expected, predicted))
print(metrics.confusion_matrix(expected, predicted))

根据结果可看出决策树分类效果最好，这是因为测试集与训练集相同。

SVM

from sklearn import metrics
from sklearn.svm import SVC

# fit a SVM model to the data
model = SVC()
model.fit(X, y)
print(model)

# make predictions
expected = y
predicted = model.predict(X)

# summarize the fit of the model
print(metrics.classification_report(expected, predicted))
print(metrics.confusion_matrix(expected, predicted))

同样由于支持向量是在测试集上学得的，故也没有错误。

优化算法参数

即常说的调参，用于选择KNN中的K，SVM中的λ等。

• 搜索法

import numpy as np
from sklearn.linear_model import Ridge
from sklearn.grid_search import GridSearchCV

# prepare a range of alpha values to test
alphas = np.array([1,0.1,0.01,0.001,0.0001,0])

# create and fit a ridge regression model, testing each alpha
model = Ridge()
grid = GridSearchCV(estimator=model, param_grid=dict(alpha=alphas))                            #GridSearchCV实现了fit，predict，predict_proba等方法，并通过交叉验证对参数空间进行求解，寻找最佳的参数。
grid.fit(X, y)
print(grid)

# summarize the results of the grid search
print(grid.best_score_)
print(grid.best_estimator_.alpha)

• 随机法
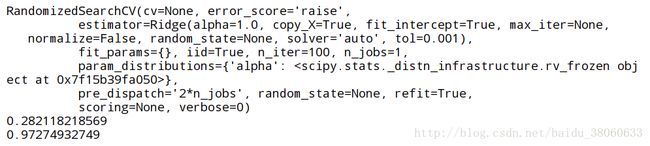
  随机从给定区间中选择参数，遍历这些参数评估算法的效果从中选择最佳的。

import numpy as np
from scipy.stats import uniform as sp_rand
from sklearn.linear_model import Ridge
from sklearn.grid_search import RandomizedSearchCV

# prepare a uniform distribution to sample for the alpha parameter
param_grid = {'alpha': sp_rand()}

# create and fit a ridge regression model, testing random alpha values
model = Ridge()
rsearch = RandomizedSearchCV(estimator=model, param_distributions=param_grid, n_iter=100)
rsearch.fit(X, y)
print(rsearch)

# summarize the results of the random parameter search
print(rsearch.best_score_)
print(rsearch.best_estimator_.alpha)

根据一份简单的入门材料做的实验分析，训练集与测试集重合，有待改进。

参考材料：
http://www.jianshu.com/p/1c6efdbce226
http://www.cnblogs.com/zhaokui/archive/2016/01/08/5112287.html