高级数据结构之K-D-TREE
k-d-tree(即k-dimensional tree)是一棵形如二叉树的一种非常重要的空间划分数据结构,尤其在多维数据访问中有重要应用。它是由Jon L. Bentley 于1975年在文献【2】中提出的,Jon L. Bentley 也是畅销书《编程珠玑》的作者。
欢迎关注白马负金羁的博客 http://blog.csdn.net/baimafujinji,为保证公式、图表得以正确显示,强烈建议你从该地址上查看原版博文。本博客主要关注方向包括:数字图像处理、算法设计与分析、数据结构、机器学习、数据挖掘、统计分析方法、自然语言处理。
------------------------------------------
一、构建k-d-tree
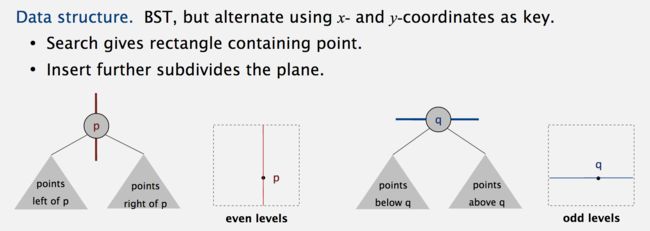
k-d树是一棵每个节点都为k维点的二叉树,其中所有非叶子节点可以视作用一个超平面把空间分区成两个半空间( Half-space )。因为有很多种方法可以选择轴垂直分区面( axis-aligned splitting planes ),所以有很多种创建k-d树的方法。 最典型的方法如下:
- 随着树的深度轮流选择轴当作分区面。(例如:在三维空间中根节点是 x 轴垂直分区面,其子节点皆为 y 轴垂直分区面,其孙节点皆为 z 轴垂直分区面,其曾孙节点则皆为 x 轴垂直分区面,依此类推。)*通常选择具有最大方差的维度k作为开始,这样以保证在这个方向上数据更为分散。
- 点由垂直分区面之轴座标的中位数区分并放入子树。
如果你觉得上面这个描述太简单,看起来还不能理解,下面我给出李航博士在文献【3】中给的描述,注意二者是完全一致的,你可以选择一个更便于自己理解的方式来参考:
这个方法产生一个平衡的k-d树。每个叶节点的高度都十分接近。然而,平衡的树不一定对每个应用都是最佳的。
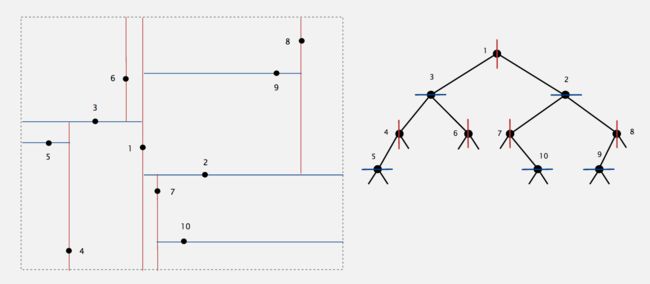
如果以k=2为例来讨论,即2-d-tree,那么上图形象地演示了建树的方法。此外,下面这个例子很好地演示了上述构建k-d-tree的过程。如下图所示,平面上共有10个点,根节点应该是垂直于x轴的分平面,所以我们从x轴方向上,找到中位数点,即点1,于是所有在x轴方向上小于点1的点(3,4,5,6)会构成它的左子树,所有在x轴方向上大于点1的点(2,7,8,9,10)会构成它的右子树。
接下来到树的(从上向下)第二层,先考虑点1的右子树,此时我们需要构建一个与 y 轴垂直的分区面以把空间划分为上下两个子空间。于是从(2,7,8,9,10)中找到一个y轴方向上的中位数,即点2,并过点2做垂直y轴的划分超平面,于是所有在y轴方向上大于点2的点(8,9)将变成点2的右子树。所有在y轴方向上小于点2的点(7,10)将变成点2的左子树。
同理,再来考虑点1的左子树,并构建一个与 y 轴垂直的分区面以把空间划分为上下两个子空间。于是从(3,4,5,6)中找到一个y轴方向上的中位数,即点3,并过点3做垂直y轴的划分超平面,于是所有在y轴方向上大于点3的点(6)将变成点3的右子树。所有在y轴方向上小于点3的点(4,5)将变成点2的左子树。
下面是维基百科上给出的另外一个例子,可以作为巩固练习之用。图中各点的坐标为(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)。
------------------------------------------
二、Range search
区域(或范围)搜索的主要目的在于找出所有位于给定axis-aligned rectangle中的点。 这时,我们主要通过执行如下三个步骤来实现:
- Check if point in node lies in given rectangle.
- Recursively search left/bottom (if any could fall in rectangle).
- Recursively search right/top (if any could fall in rectangle).
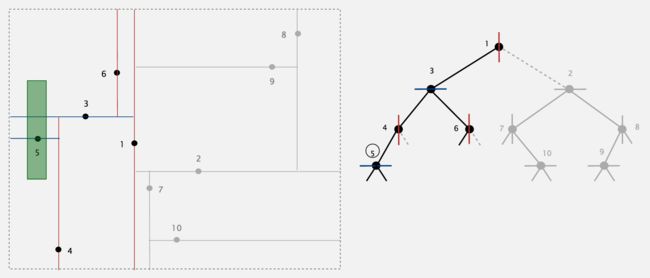
来看下面这个例子。从根节点开始,我们检查点1是否在矩形框里,答案是不在。于是我们继续检查它的子树。因为矩形框位于点1的左侧(也就是说框中的点在x轴方向上要小于点1),于是继续搜索其左子树,而直接忽略其右子树。
接下来我们检查点3(也就是点1的孩子节点),答案是不在。于是我们继续(递归地)检查它的子树。但是因为矩形框横跨由过点3的超平面所划分的上下两个子空间,所以我们要继续搜索它的左右两个子树。
如此递归地搜索下去,最后就会发现点5位于矩形框中。
标准情况下,Range Search的时间复杂度是R+logN,其中R是要返回的点的数量,N是空间中点的总数。
最糟糕的情况下,Range Search的时间复杂度是R+sqrt(N)。
------------------------------------------
三、Nearest neighbour search
最邻近搜索用来找出在树中与输入点(或目标点)x最接近的点,具体方式在描述上略有差异(但本质上是相同的):可以是自顶向下的(例如文献【4】)算法会在向下找的时候直接做剪枝,也可以是自下向上的(例如文献【3】),算法会在向上回溯的时候再考虑剪枝。我们下面的介绍基本属于后者。
k-d树最邻近搜索的算法如下:
1. 从根节点开始,递归的往下移。往左还是往右的决定方法与(构建新树时)插入元素(目标元素x)的方法一样(如果输入点在分区面的左边则进入左子节点,在右边则进入右子节点)。
2. 一旦移动到叶节点,将该节点当作"当前最邻近点"。
3. 解开递归向上回退,并对每个经过的节点递归地执行下列步骤:
1)如果目前所在点比"当前最邻近点"更靠近输入点,则将其变为当前最邻近点。
2)检查目前所在点的子树有没有更近的点,如果有则从该节点往下找。更具体地说,(要不要搜索某一边的子树需要)检查当前的分割超平面与“目标点为球心,以目标点与“当前最邻近点”间距离为半径的超球体”是否相交。
a)如果相交,可能在该子树对应之区域内存在距离目标点更近的点,移动到该子树,接着递归地进行最近邻搜索;
b)如果不相交,向上回退。4. 当回退到根节点时,搜索结束。最后的“当前最邻近点"即为x的最近邻点。
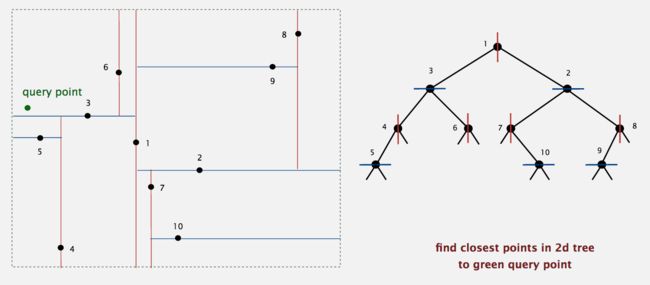
我们还是来看一个例子。目标点x即图中的绿色query points。现在我们要找到k-d-tree中离这个目标点x最近的点。
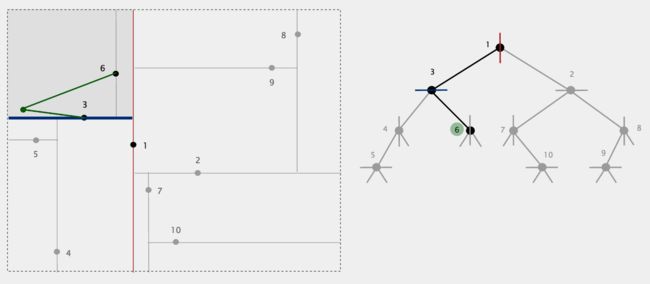
按照算法描述的规则,我们首先从根节点开始搜索,因为点x位于由点1确定的超平面的左侧,所以进入右子节点。接下来,因为点x位于点3的上方,所以进入点3的右子节点。由于点6是叶节点,所以将该节点当作"当前最邻近点"。然后
解开递归向上回退,经过节点3,计算点x到点3的距离,发现目前所在点3比"当前最邻近点"6更靠近输入点x,则将3变为当前最邻近点。
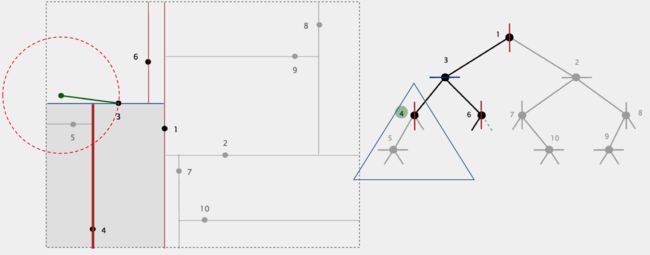
现在我们考虑是否要检测点3的左子树以获取更佳的最近邻。由于我们是想讨论节点3的左子树中是否有更佳的最近邻,而节点3的左子树对应的区域是节点3所确定的分割超平面的下方。所以我们就是要看以x为球心,以x到点3的距离为半径的球(或者圆)是否与节点3所确定的分割超平面的下方区域有交叉。所以根据算法描述,我们检查由3确定分割超平面与“目标点x为球心,以目标点x与“当前最邻近点”3之间距离为半径的超球体”是否相交。显然相交,所以需要搜索节点3的左子树。
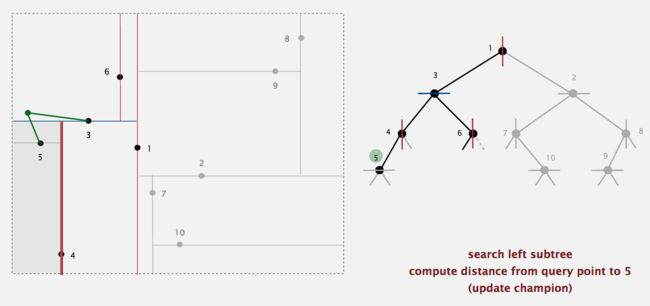
节点3的左子树由上图中右侧的蓝色三角标识出。对于现在经过的节点4,计算点x到点4的距离,显然大于当前距离,所以无需更新"当前最邻近点"。但我们还要考虑是否继续搜寻节点4的左右子树。于是我们检查由4确定分割超平面与“目标点x为球心,以目标点x与“当前最邻近点”3之间距离为半径的超球体”是否相交。显然相交,所以需要搜索节点4的左右子树。但是其右子树为空,可不考虑。
对于节点4的左子树,计算从点5到目标点x的距离,发现比之前的(从3到x的)距离短,所以将5更新为"当前最邻近点"。
然后算法回退到节点4,到节点3,节点3的左右子树及其本身都已考察过,继续回退到节点1。对于节点1,其左子树已经考察完毕,我们考虑是否要检测它的右子树。检查由1确定分割超平面与“目标点x为球心,以目标点与“当前最邻近点”5之间距离为半径的超球体”是否相交。显然不相交,所以不需要搜索节点1的右子树。最后计算从点1到目标点x的距离,发现不比之前的(从5到x的)距离短,所以不更新最邻近点。
因为我们已经回退到根节点,搜索结束。最后的“当前最邻近点"5即为x的最近邻点。
为了防止太长的文章让你感到心烦意乱,文件到此就告一段落。在之后的文章里,我会结合代码再来讨论一下k-d-tree的实现和在解决实际问题中的功用。(本文章中的例子及图示均引自参考文献中的资料,特此说明)
------------------------------------------
参考文献及推荐阅读材料
【1】 https://en.wikipedia.org/wiki/K-d_tree
【2】 Bentley, J. L. (1975). "Multidimensional binary search trees used for associative searching". Communications of the ACM. 18 (9): 509-517.
【3】 李航. 统计学习方法,清华大学出版社,2012.
【4】 普林斯顿大学教授Robert Sedgewick(他也是Knuth的高徒)讲授的公开课,https://www.youtube.com/watch?v=uf1ky464340
【5】 Volker Gaede, Oliver Günther. Multidimensional Access Methods. ACM Computing Surveys, Vol. 30, No. 2, June 1998.