广东航空大数据创新大赛：机场停机位资源分配优化

Another url：https://bulihanjie.github.io/2017/01/01/机场停机位资源分配优化/

题目描述

https://tianchi.shuju.aliyun.com/outsource/offer/projectdetails.htm?spm=5176.8199929.0.0.nPvIru&id=3092
机场每天都有大量的航班起降，每个航班降落以后都会分配到一个指定的机位进行保障，保障结束以后再离开进行下一航段。为了保障每个航班都有相应的机位，机场会提前安排好第二天的所有飞机机位资源。

成绩

复赛：得分14.40，排行榜第一名；
决赛：第一名

总体思路

1、 求解初始解：使用贪心算法快速得到一个可行解
2、 优化解：使用优化算法对初始解进行优化，我们采用的优化算法是破坏与重建算法

贪心算法

按时间顺序遍历每个航班，对每个航班执行下面操作：尝试安排到其可安排的机位中，若当前机位能安排（能安排代表满足各种约束）就直接安排，若没有机位能安排当前航班，则当前航班不安排。
只需不到1秒的时间，生成了13.28的初始可行解。

破坏与重建算法

步骤一、对一个已知的初始解，破坏掉一些已经被安排的航班，即一个破坏过程；
步骤二、对剩下已经安排的航班其机位保持不变，将当前所有未安排的航班使用线性规划模型求解当前情况下的最优解，即一个重建过程；
步骤三、重复此破坏与重建过程，持续对解进行优化，直到满足一个停止条件。

算法评价：此算法通过破坏可以打破局部约束，使其可以达到一个更优的解；通过线性规划模型进行重建，使其可以得到当前情况下的最优解，这个解不会比初始解差；由于已分配机位的航班在时间上是均匀分布，影响剩下航班的分配，因此未分配的航班虽多但重建效率很快。

线性规划模型

变量

二进制变量$g_{ij}\in G$表示航班分配机位的情况：
$$g_{ij}=\{\begin{array}{ll}1& \text{航班i分配到机位j}\\ 0& \text{航班i没有分配到机位j}\end{array}$$
滑道冲突的计算与机位的入滑道和出滑道有关，但和具体机位是无关的，具体不同滑道可以表示为$p_k\in P$;
二进制变量$d_{ik}\in D$表示航班滑道冲突的情况：
$$d_{ik}\in \{\begin{array}{ll}1& \text{航班i的滑道为pk，且和其它航班滑道冲突}\\ 0& \text{航班i的滑道非pk，或和其它航班没有滑道冲突}\end{array}$$
每个航班的旅客人数用$h_i\in H$来表示，总的旅客人数为$h_{sum}={\sum }_i{h}_i$；
定义总的航班数量为$n$，总的机位数量为$m$；

目标函数

$$\begin{gathered} F(G,P,D)=max\sum _{i,j}10\times \frac{g_{ij}}{n}+3\times \frac{g_{ij}\times 1 \\ 机位j是近机位 \\ }{n}+3\times g_{ij}\times 1 \\ 机位j是近机位 \\ \times \frac{h_i}{h_{sum}}-1\times \frac{g_{ij}\times 1 \\ 机位j是临时机位 \\ }{n}-\sum _{i,k}1\times \frac{d_{ik}}{n} \end{gathered}$$

约束条件

1. 对于初始固定的航班添加约束：$$\forall i,j航班i预先分配到机位j⟶g_{ij}=0$$$$\forall i航班i不分配机位⟶\forall j,g_{ij}=0$$
2. 保证每个航班只会分配一个机位：
   $$\forall i⟶\sum _j{g}_{ij}\le 1$$
3. 保证航班只能分配到可以分配的机位：
   $$\forall i,j航班i不能分配到机位j⟶g_{ij}=0$$
4. 保证在同一个机位上的航班满足十分钟约束：
   $$\forall i_1,i_2,j且航班i_1和航班i_2不满足十分钟约束⟶g_{i_{1}j}+g_{i_{2}j}\le 1$$
5. 保证在机位发生重合时也满足十分钟约束：$$\forall i_1,i_2,j_1,j_2且机位j_1和机位j_2重合，航班i_1和航班i_2不满足十分钟约束⟶g_{i_1{j}_1}+g_{i_2{j}_2}\le 1$$
6. 保证分配方案满足阻挡的约束：$$\forall i_1,i_2,j_1,j_2且航班i_1在机位j_1阻挡航班i_2进入机位j_2⟶g_{i_1{j}_1}+g_{i_2{j}_2}\le 1$$
7. 滑道冲突约束，航班的滑道冲突和分配的机位相关：$$\begin{gathered} \forall i,k⟶\sum _j{g}_{ij}\times 1 \\ 机位j的滑道为p_k \\ \ge d_{ik} \end{gathered}$$
8. 滑道冲突约束，当航班分配了机位且存在滑道冲突时，$d_{i}k$为1,$c$是一个很大的常数：$$\begin{gathered} \forall i,k⟶\sum _j{g}_{ij}\times 1 \\ 机位j的滑道为p_k \\ +\sum _{i_1̸=i,j_1}\frac{g_{i_1{j}_1}\times 1 \\ 航班i在滑道k与航班i_1在滑道j_1滑道冲突 \\ }{c}\le d_{ik} \end{gathered}$$
   
   

模型优化

1. 机位冲突优化：
   对于上面的第4个约束，同一机位的航班满足10分钟约束，以及第5个约束，机位发生重合时满足十分钟约束，可以换一种思路去考虑，换成:任何一个位置在任何一个时刻最多只有一架飞机，一个飞机占用这个位置的时间为$$\begin{gathered} [in{ \\ }_{t}ime,out{ \\ }_{t}ime+10) \end{gathered}$$,也既是：$$\forall i_1,i_2,...,i_n,j_1,j_2,\dots ,j_m且航班i_1到航班i_n包含同一个时刻，机位j_1到机位j_n包含同一个位置⟶\sum _j\sum _i{g}_{ij}\le 1$$
   进行这样的优化后，将很多的单独的约束合并为一个约束了，模型占用的内存减少了很多，数据中独立的时刻只有1800多个。
2. 滑道冲突优化：
   对于滑道冲突的约束计算，假如是通过枚举两个航班和其分配的两个机位来判断冲突，时间复杂度为$O(n^2{m}^2)$，这样的计算造成运行效率低和内存消耗大。
   在我们的方法中，滑道约束8的计算只需要枚举两个航班以及对应的滑道即可，滑道的数量远小于机位的数量，极大的提高了运行效率以及降低内存消耗。

破坏方式

不同的破坏方式，打破局部约束的能力不一样，所以我们制定了三种基本的破坏方式：

1. 随机航班破坏：随机选取一些航班进行破坏
2. 随机机位破坏：随机选取一些机位，对机位下的航班进行破坏
3. 随机时间破坏：随机选取一个时间段，对这个时间段上的航班进行破坏
   这三种破坏方式，在破坏相同比例航班的基础上，各自的效果各不相同，我们从重建速度，收敛性两个方面进行比较发现：

type	重建速度	收敛
航班破坏	快	中
机位破坏	中	快
时间破坏	慢	慢

在实际使用中，我们主要会采取航班破坏和机位破坏，我们最后的程序中，可以根据自己的实际情况，制定不同的破坏与重建策略。

算法效果研究

我们使用机位破坏，每次破坏1/15的机位，迭代了10000次，运行了6个小时，每次大约2.2秒，最后结果到了14.38，下面是运行结果图：

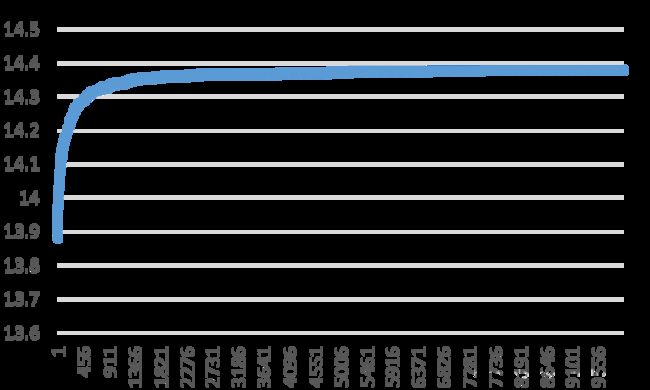
可以看到前期收敛是非常快的，迭代500次，就到达了14.3，大约用时20分钟。不过后面的收敛就非常的缓慢了。
当加大破坏比例后，其收敛能够加快，这里没有数据了，这是我们多次实践的经验结果，具体的详细研究还需要很多的时间。
在对算法的各种性质进行深入实验研究后，可以根据各种不同破坏方式下破坏不同比例的性质的不同，制定最优策略，以达到更快的得到更好的解的目的，目前的策略只是一个感性的策略，根据的是经验。

最优结果说明

目前的最优解可以说是我们在进行实验过程中得到的解，我们曾经想到的各种优化方案，都曾经应用到了产生这个解的过程中。还有我们在优化的过程中也是断断续续的跑的，白天要上班或上课，电脑不能跑，到晚上才能跑，所以具体目前得到这个解跑了多久，我们也是不清楚的。
现在要复现这个解也是可以复现，按照现在的算法，只要设置对相应的破坏与重建策略，肯定可以到达现在的解，只是时间问题，因为越到后面收敛是越来越慢的，其实到14.399我们只花了一个晚上了时间，但是到现在的14.4008花了好多个晚上。

比赛总结

在比赛的过程中也不是一帆风顺的，前期的工作也尝试过各种不同的方法：

• 数据规模增大，尝试过对航班分块处理提高算法的效率；
• 采用对时间的滑窗来对跑线性规划，得到14.25；
• 用禁忌搜索来优化解，得到14.27；

正是比赛中对各种方法的尝试逐渐增加了对问题、模型的理解，最终得到了一个线性规划与破坏重建结合的算法。比赛收获良多，我们也享受比赛过程中不断进步的喜悦。