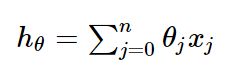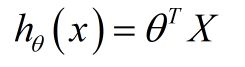梯度下降法及其python实现
梯度下降
假设函数
损失函数
1.批量梯度下降(BGD)



每次参数更新的伪代码如下:
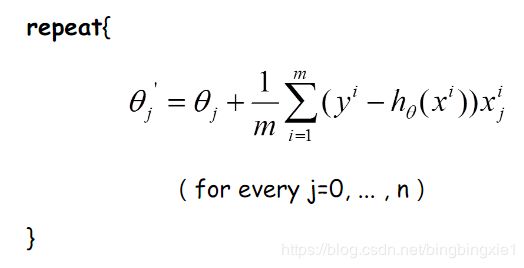
由上图更新公式我们就可以看到,我们每一次的参数更新都用到了所有的训练数据(比如有m个,就用到了m个),如果训练数据非常多的话,是非常耗时的。
下面给出批量梯度下降的收敛图:
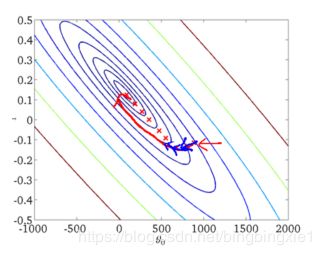
从图中,我们可以得到BGD迭代的次数相对较少。
2.随机梯度下降法(SGD)
由于批梯度下降每跟新一个参数的时候,要用到所有的样本数,所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度,来更新θ:
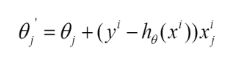
更新过程如下:

随机梯度下降是通过每个样本来迭代更新一次,对比上面的批量梯度下降,迭代一次需要用到所有训练样本(往往如今真实问题训练数据都是非常巨大),一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
随机梯度下降收敛图如下:
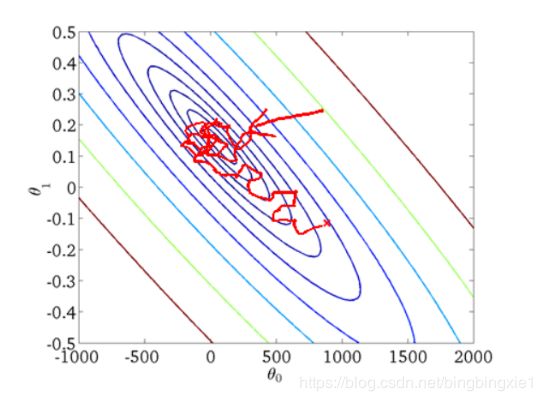
我们可以从图中看出SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。但是大体上是往着最优值方向移动
3. min-batch 小批量梯度下降法(MBGD)
我们从上面两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
更新伪代码如下:
我们假设每次更新参数的时候用到的样本数为10个(不同的任务完全不同,这里举一个例子而已)
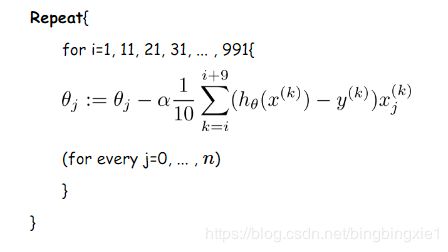
python代码:
# -*- coding: utf-8 -*-
# @Time : 2018/9/26 19:16
# @Author : Bing
# @FileName: temp.py
import numpy as np
import random
def gen_line_data(sample_num=100):
"""
y = 3*x1 + 4*x2
:return:
"""
x1 = np.linspace(0, 9, sample_num)
x2 = np.linspace(1, 10, sample_num)
x3 = np.linspace(2, 11, sample_num)
x = np.concatenate(([x1], [x2], [x3]), axis=0).T
y = np.dot(x, np.array([3, 4, 5]).T) # y 列向量
return x, y
# 批量梯度下降
def bgd(samples, y, step_size=0.01, max_iter_count=10000):
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float64)
loss = 10
iter_count = 0
while loss > 0.00001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float64)
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
for j in range(dim):
error[j] += (y[i] - predict_y) * samples[i][j]
for j in range(dim):
w[j] += step_size * error[j] / sample_num # 批量更新权重 w
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w
# 随机梯度下降
def sgd(samples, y, step_size=0.01, max_iter_count=10000):
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float64)
loss = 10
iter_count = 0
while loss > 0.00001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float64)
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
for j in range(dim):
error[j] += (y[i] - predict_y) * samples[i][j]
w[j] += step_size * error[j] / sample_num # 每一个样本更新一次权重 w
# for j in range(dim):
# w[j] += step_size * error[j] / sample_num
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w
# 小批量梯度下降
def mbgd(samples, y, step_size=0.01, max_iter_count=10000, batch_size = 0.2):
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float64)
loss = 10
iter_count = 0
while loss > 0.00001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float64)
# 随机选取小批量数据
index = random.sample(range(sample_num), int(np.ceil(sample_num * batch_size)))
batch_samples = samples[index]
batch_y = y[index]
for i in range(len(batch_samples)):
predict_y = np.dot(w.T, batch_samples[i])
for j in range(dim):
# 计算小批量数据的损失函数
error[j] += (batch_y[i] - predict_y) * batch_samples[i][j]
# 更新小批量的权重
for j in range(dim):
w[j] += step_size * error[j] / len(batch_samples)
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w
if __name__ == '__main__':
samples, y = gen_line_data()
print(samples[0])
print(samples[1])
w = sgd(samples, y)
print(w) # 会很接近[3, 4, 5]
参考资料:
https://www.cnblogs.com/wyuzl/p/7645602.html