数据结构与算法之二叉堆训练营

前言： 二叉堆本质上就是一个特殊的完全二叉树。其中，“特殊”表现在节点元素之间存在着大小规律，完全二叉树表示二叉堆的存储结构采用数组实现，只要记住这两点，二叉堆就不难理解和实现；二叉堆根据大小规律的不同，可以分为大顶堆和小顶堆。

二叉堆篇

概念简述： 二叉堆是一种完全二叉树，在这棵树中，任意父节点的值全部大于等于（小于等于）其子节点的值；其中如果任意父节点的值大于等于子节点的值，则该二叉堆就是大顶堆；如果任意父节点的值小于等于子节点的值，则该二叉堆就是小顶堆。本文以小顶堆为例，讲述小顶堆的相关关键操作以及二叉堆的应用–堆排序与优先队列！

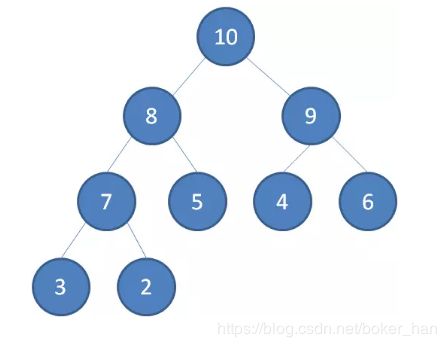
前面说到，二叉堆是一种特殊的完全二叉树，那么对于完全二叉树我们可以利用完全二叉树的结构特点使用数组来实现；而如何将一棵普通的完全二叉树调整为小顶堆，就是我们接下来的主要讲述的内容。首先，对于一棵二叉树来说，我们在使用时除了查找和遍历之外，最常使用的操作就是插入和删除节点。那么，对于二叉堆（小顶堆）的构建我们同样先着手这两种操作的实现！

---

插入操作： 对于二叉堆的元素插入，我们可以将其看作为是在数组的末尾，也就是最后一个叶子结点的右边插入；如下图所示，节点0就是插入的节点元素，对于插入之后的二叉树结构已经不满足小顶堆的定义，所以我们需要对其进行调整，我们采用上浮新节点来将插入节点后的二叉树调整为小顶堆；

实现代码如下：

		 //向小顶堆中插入节点之后，所需的调整操作
	    public static void upAdjust(int[] heapArray){
	            int childIndex = heapArray.length - 1;//当前插入节点在数组中的下标
	            int parentIndex = (childIndex - 1) / 2;//当前插入节点的父节点在数组中的下标
	            //保留新插入节点的值用于最后的赋值
	            int temp = heapArray[childIndex];
	            //循环上调，使完全二叉树变为小顶堆
	            while(childIndex > 0){
	                //如果当前父节点的元素小于等于子节点的元素，此时已经调整为小顶堆，结束调整
	                if(heapArray[parentIndex] <= temp)
	                    break;
	                //父节点与子节点大小不满足小顶堆的定义，进行上浮调整
	                heapArray[childIndex] = heapArray[parentIndex];
	                //更新父、子节点，再次进行调整
	                childIndex = parentIndex;
	                parentIndex = (childIndex - 1) / 2;
	            }
	            //将插入节点的值赋值到最后的位置
	            heapArray[childIndex] = temp;
	    }

删除操作： 对于二叉堆的删除，指的是将堆顶元素删除，可以看作是删除数组的第一个元素；如左图所示，在删除堆顶元素之后，我们需要将堆底元素变为堆顶元素，如右图所示；

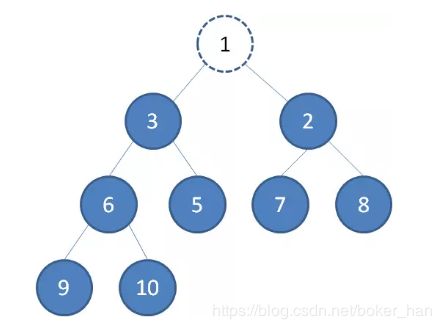
实现代码如下：

	  	//向小顶堆删除节点之后，所需的调整操作
	    public static void downAdjust(int[] heapArray,int begin,int end){
	            int parentIndex = begin;//当前堆顶元素所在的下标
	            int childIndex = 2 * parentIndex + 1;//堆顶元素做节点的下标
	            //保留堆顶节点的值用于最后的赋值
	            int temp = heapArray[parentIndex];
	            while(childIndex < end){
	                //找出左右子节点中最小的节点，并更新childIndex
	                if(childIndex + 1 < end && heapArray[childIndex] > heapArray[childIndex+1]){
	                    childIndex++;
	                }
	                //如果当前父节点的元素小于等于子节点的元素，此时已经调整为小顶堆，结束调整
	                if(temp <= heapArray[childIndex]){
	                    break;
	                }
	                //父节点与子节点大小不满足小顶堆的定义，进行下沉调整
	                heapArray[parentIndex] = heapArray[childIndex];
	                //更新父、子节点，再次进行调整
	                parentIndex = childIndex;
	                childIndex = 2 * parentIndex + 1;
	            }
	            //将堆顶节点的值赋值到最后的位置
	            heapArray[parentIndex] = temp;
	    }

构建小顶堆： 对于一个普通完全二叉树，将其调整为一个小顶堆，此过程即为二叉堆的构建。采用的方法是对所有非叶子节点进行下沉调整，直至所给二叉树变为小顶堆；
实现代码如下：

    public static void buildHeap(int arr[]){
               if(arr == null || arr.length <= 1)
                   return;
               int len = arr.length;
               int begin = (len - 2) / 2;
               for(int i = begin ; i >= 0 ; i--)
                   downAdjust(arr,i,len);
       }

---

以上是关于二叉堆以及二叉堆的关键操作和构建的讲解，下面看一下，二叉堆这一数据结构的实际应用；首先，我们利用二叉堆是一个特殊的完全二叉树的性质来讲一下堆排序，因为基本上超越基本的排序算法（冒泡、选择、插入排序等）的高级排序都与二叉树这个结构有着千丝万缕的关系！

堆排序篇

话不多说，直接说一下如何利用二叉堆来实现堆排序，首先，我们需要将待排序的数组看作为一棵完全二叉树，那么，对这个待排序的数组（完全二叉树），我们需要做的是，将其调整为一个二叉堆；之后我们就可以利用二叉堆的性质——堆顶元素为二叉堆中最大或最小的元素，将当前堆顶元素与数组末端元素调换，如下图所示；再对位于刚被置换到尾部的最大值之前的元素进行堆调整，然后再次调换，直至只剩下一个堆顶元素为止，我们就完成了堆排序！

堆排序可以分为两部分：

1. 将数组初始化为大顶堆
2. 交换堆顶元素和堆尾元素，并对除堆尾元素以外的其余堆元素进行堆调整；以此往复，直至剩余的堆元素为1时，堆排序结束

实现代码如下：

    public static void heapSort(int[] arr){
           if(arr == null || arr.length <= 1)
               return;
           //初始化数组为二叉堆
           for(int i = (arr.length - 2) / 2 ; i >= 0 ; i--){
               downAdjust1(arr,i,arr.length);
           }
           //交换堆顶元素以及堆调整
           heapSortCore(arr,0,arr.length - 1);
       }
       //交换堆顶元素以及堆调整核心逻辑实现
       private static void heapSortCore(int[] arr, int begin, int end){
           //循环执行交换元素+堆调整操作，直至只剩下一个元素为止
           while(end > begin){
               arr[begin] = arr[begin] + arr[end];
               arr[end] = arr[begin] - arr[end];
               arr[begin] = arr[begin] - arr[end];
               end--;
               if(begin != end){
                   downAdjust1(arr,begin,end+1);
               }
           }
       }
       //下沉调整堆结构
       private static void downAdjust1(int[] arr,int begin,int end){
           int parentIndex = begin;
           int childIndex = parentIndex * 2 + 1;
   
           int temp = arr[begin];
           while(childIndex < end){
               if(childIndex + 1 < end && arr[childIndex + 1] > arr[childIndex]){
                   childIndex++;
               }
               if(temp >= arr[childIndex]){
                   break;
               }
               arr[parentIndex] = arr[childIndex];
               parentIndex = childIndex;
               childIndex = parentIndex * 2 + 1;
           }
           arr[parentIndex] = temp;
       }

---

优先队列篇

优先队列是一种特殊队列，在满足先进先出的特点的基础之上，实现了每一次出队的元素是队列中元素的最值；联想二叉堆的特点以及关键操作——插入和删除，完全契合优先队列的定义，下面直接给出代码实现（注意：代码只实现了基本的入队和出队操作，并没有提供数组扩容的相关实现）：

   	 public class PriorityQueue {
   	    private int[] elements;
   	    private int counts;
   	
   	    public PriorityQueue(int size){
   	        elements = new int[size];
   	    }
   	    //入队
   	    public void offer(int element){
   	        elements[counts++] = element;
   	        if(counts > 1)
   	            upAdjust(elements,0,counts);
   	    }
   	    //出队
   	    public int poll(){
   	        if(counts == 0)
   	            return -9999;
   	        int result = elements[0];
   	        elements[0] = elements[0] + elements[counts];
   	        elements[counts] = elements[0] -elements[counts];
   	        elements[0] = elements[0] - elements[counts];
   	        counts--;
   	        downAdjust();
   	        return result;
   	    }
   	    //插入时进行上浮调整
   	    private void upAdjust(int[] arr,int begin,int end){
   	        int childIndex = end - 1;
   	        int parentIndex = (childIndex - 1) / 2;
   	        int temp = arr[childIndex];
   	        while(childIndex > 0){
   	            if(temp <= arr[parentIndex])
   	                break;
   	            arr[childIndex] = arr[parentIndex];
   	            childIndex = parentIndex;
   	            parentIndex = (childIndex - 1) / 2;
   	        }
   	        arr[childIndex] = temp;
   	    }
   	    //删除时进行下沉调整
   	    private void downAdjust(){
   	        int parentIndex = 0;
   	        int childIndex = parentIndex * 2 + 1;
   	        int temp = elements[0];
   	        while(childIndex <= counts){
   	            if(childIndex + 1 <= counts && elements[childIndex] < elements[childIndex + 1]){
   	                childIndex++;
   	            }
   	            if(elements[childIndex] <= elements[parentIndex])
   	                break;
   	            elements[parentIndex] = elements[childIndex];
   	            parentIndex = childIndex;
   	            childIndex = parentIndex * 2 + 1;
   	        }
   	        elements[parentIndex] = temp;
   	    }
   	
   	    public static void main(String[] args){
   	        PriorityQueue priorityQueue = new PriorityQueue(6);
   	        priorityQueue.offer(2);
   	        priorityQueue.offer(5);
   	        System.out.println(priorityQueue.poll());
   	        priorityQueue.offer(1);
   	        priorityQueue.offer(7);
   	        priorityQueue.offer(6);
   	        System.out.println(priorityQueue.poll());
   	        priorityQueue.offer(10);
   	        priorityQueue.offer(19);
   	        System.out.println(priorityQueue.poll());
   	    }
   }  

至此，本文对二叉堆以及二叉堆的应用给予了分析和实现，其实，在学习数据结构和算法的过程中，最好能够做到知其然，知其所以然，这样才能更深入地领悟数据结构与算法的美~