公钥密码的基本原理

公钥密码：基于数学函数而非基于代替和置换；公钥密码使用两个独立的密钥。

公钥密码术语：

1. 非对称密钥：公钥和私钥，用来加密和解密，或用来生成签名或验证签名；
2. 公钥证书：是有签证机构用自己的私钥签名的数字文件；
3. 公钥密码算法：从公钥推私钥是不可行的；
4. 公钥基础设施（PKI）：用于管理证书，公私钥对，并负责产生，维护和废除公钥证书的集合。

公钥密码学解决了传统密码学中最困难的两个问题：1）密钥分配问题；2）数字签名问题。
对称密码进行密钥分配的要求：

1. 通信双方已共享一个密钥，而该密钥已通过某种方法分配给通信双方；
2. 利用密钥分配中心（key distribute center，KDC）。

数字签名问题：因为私钥是信息发送者才拥有的密钥，所以可以通过该特性来确定某个信息是否从信息发送者发出的，即实现了“签名“。

公钥密码体制

特点：

1. 仅根据密码算法和加密密钥来确定解密密钥从计算上是不可行的；
2. 两个密钥中任何一个都可用来加密，另一个用来解密。

组成部分：

1. 明文
2. 加密算法
3. 公钥和私钥
4. 密文
5. 解密算法

步骤：

1. 每个用户产生一对密钥，用于加密和解密；
2. 每个用户将其中一个密钥公开，该密钥称为 公钥；另一密钥保持私密，该密钥称为 私钥；
3. 若B要给A发送消息，则B用A的公钥对信息加密；
4. A收到后用A的私钥解密。因为只有A直到私钥，故其他人无法解密。

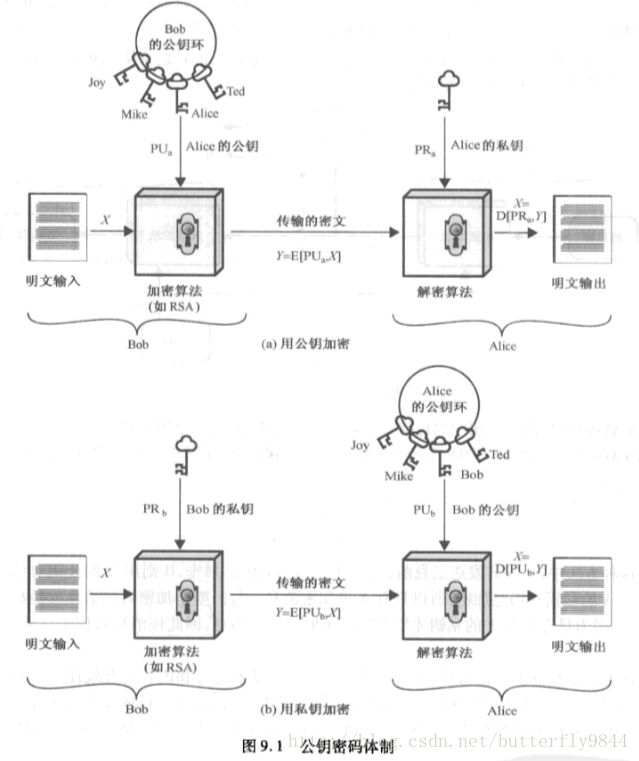
如图9.1（a）所示，即为上述加密传输步骤的图示。A的公钥谁都可以访问，而A的私钥只有自己知道，在不暴露的情况下该传输就是安全的。
Y = E(PUb, X)
X = D(PRb, Y)
其中
X：明文
Y：密文
PUb：B的公钥（Public Key）
PRb：B的私钥（Private Key）

如图9.1（b）所示，使用私钥进行加密可以实现认证功能。
Y＝E(PRa, X)
X＝E(PUa, Y)
A向B发送通过A的私钥PRa加密的信息，B用A的公钥PUa解密。由于用A的私钥对信息加密，所以只有A可加密信息，因此整个加密后的信息就是数字签名，可用于认证源和数据完整性。

为提高效率，只对一段称为“认证符“的数据加密，是该信息的函数，一旦信息修改则引发认证符的变化。若对认证符加密，则结果可作为数字签名来验证信息源，信息和通信序列的有效性。
但注意！因为认证方式是用私钥加密，公钥解密，而公钥和加密后的信息都能够被攻击者接收到，因此用私钥加密的信息不具备保密性。除此之外，除了认证符外部分都是明文信息故这部分也不具有保密性。

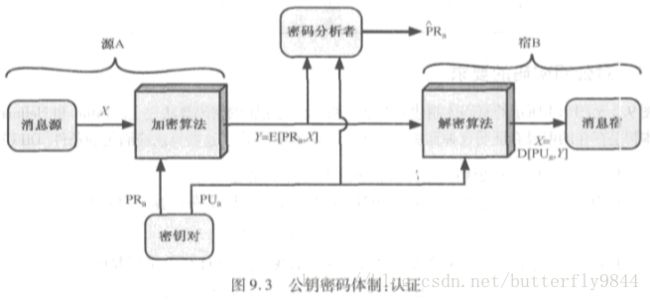
解决方法：两次公钥加密。
Z＝E(PUb, E(PRa, X))
X＝D(PUa,D(PRb, X))

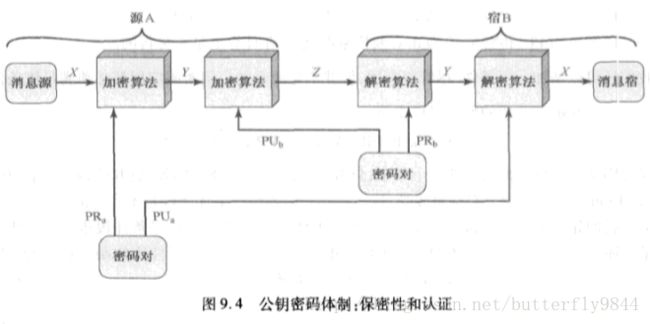
即对A的数字签名再用B的公钥加密，这样只有B可以用其私钥进行解密得到A的数字签名，再用A的公钥解密检查是否正确。

公钥密码体制的应用

• 加密/解密：用对方公钥加密，对方用自己私钥解密。
• 数字签名：发送方用自己私钥对信息加密，接收方用发送方公钥解密。加密的信息可以为整个消息，也可为认证符，认证符是整个信息的函数。
• 密钥交换：通信双方交换会话密钥，使用了通信一方或双方的私钥。

常用算法的支持：

对公钥密码的要求

分析：
要想满足上述条件，关键是一个单向陷门函数。
单向函数：每个函数值存在唯一的拟，但计算函数值容易，求逆不可行。（函数概念里的双射条件：单射＋满射的一一映射，但是从变量到值可算，值到变量不可算）
单向陷门函数：一个函数若计算函数值很同意，并在缺少一些附加信息时计算函数的逆是不可行的，但是已知这些附加信息时，可在多想是时间内计算出函数的逆。

映射关系如下所示：

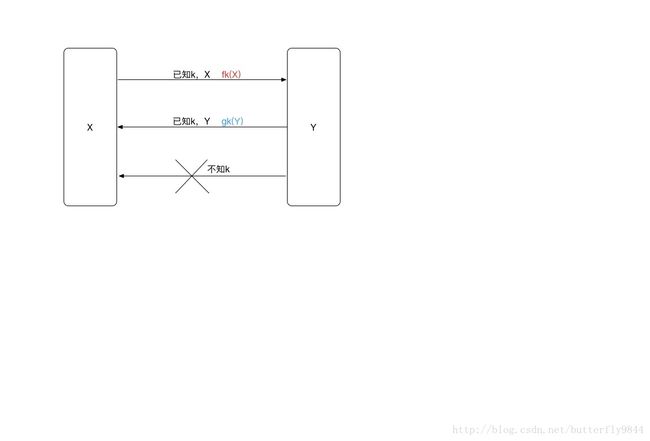
(其中gk(Y)是fk(X)的你逆函数)
我觉得可以这样理解：
X：明文；
Y：密文；
fk(X)：公钥；
gk(Y)：私钥；
k：加密算法输入。
其中gk(Y)函数公开，发送方用k，加密算法和接收方的fk(X)加密，接收方用k，加密算法和gk(Y)解密。

对公钥密码的攻击

1. 穷举攻击：密钥长度可增加穷举攻击的难度，但加／解密太慢，公仅限于密钥管理和签名中；
2. 从给定的公钥计算出私钥的方法；
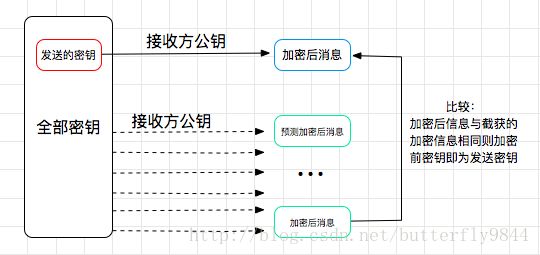
3. 穷举消息攻击：比如传输56位DES密钥，用公钥对所有可能的密钥加密，并与传送的密文匹配从而解密任何信息，解决方法为消息后面附加随机数。

穷举消息攻击：

总结

这一部分简单介绍了公钥的相关原理，用接收方公钥加密则为发送保密信息，用自己私钥加密既可用于数字签名；公钥密码的关键技术是找到一个单向陷门函数；同时介绍了哪些算法支持哪些应用以及对于公钥密码的攻击手段。下一节将主要讲解公钥密码中广泛使用的RSA算法。