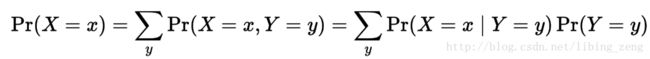信息科学原理第一章(香农熵,条件熵,相对熵)
@(信息科学原理)
- 导论
- 香农熵
- 联合熵
- 互信息
- 条件熵
- 相对熵(KL-散度)
- 交叉熵
- 边缘概率,条件概率,联合概率
- - 条件概率计算的是 P(y|x)=P(x,y)P(x) P ( y | x ) = P ( x , y ) P ( x )
- example
- 香农熵
导论
香农熵
信息: h(x)=−logp(x) h ( x ) = − log p ( x )
H(X,Y)=−∑x∈XP(x)log(P(x))=Ex∼Plog(P(x)) H ( X , Y ) = − ∑ x ∈ X P ( x ) log ( P ( x ) ) = E x ∼ P l o g ( P ( x ) )
其中 0log0=0 0 log 0 = 0 ,并且定义 log1e=1nats log 1 e = 1 n a t s 和 log12=1bits log 1 2 = 1 b i t s
联合熵
H(X,Y)=−∑x∈X,y∈YP(x,y)logP(x,y)=Ex∼PlogP(x,y) H ( X , Y ) = − ∑ x ∈ X , y ∈ Y P ( x , y ) log P ( x , y ) = E x ∼ P log P ( x , y )
互信息
I(X,Y)=∑x∈X,y∈YP(x,y)logP(x,y)P(X)P(Y)=Ex,y∼PlogP(x,y)P(X)P(Y)=DKL(P(x,y)∣∣P(X)P(Y)) I ( X , Y ) = ∑ x ∈ X , y ∈ Y P ( x , y ) log P ( x , y ) P ( X ) P ( Y ) = E x , y ∼ P log P ( x , y ) P ( X ) P ( Y ) = D K L ( P ( x , y ) ∣∣ P ( X ) P ( Y ) )
衡量两个信息的相关性大小的量
条件熵
H(Y|X)=−∑x∈X,y∈YP(x,y)logP(y|x)=−∑x∈X,y∈YP(x,y)logP(x,y)P(x)=∑x∈X,y∈YP(x,y)logP(x)P(x,y)=Ex,y∼PlogP(x)P(x,y) H ( Y | X ) = − ∑ x ∈ X , y ∈ Y P ( x , y ) log P ( y | x ) = − ∑ x ∈ X , y ∈ Y P ( x , y ) log P ( x , y ) P ( x ) = ∑ x ∈ X , y ∈ Y P ( x , y ) log P ( x ) P ( x , y ) = E x , y ∼ P l o g P ( x ) P ( x , y )
知道的信息越多,随机事件的不确定性就越小
proof: H(X,Y)=H(X)+H(Y|X) H ( X , Y ) = H ( X ) + H ( Y | X ) :
H(X,Y)=−∑x∈X,y∈YP(x,y)logP(x,y)=−∑x∈X,y∈YP(x,y)log[P(y|x)P(x)]=−∑x∈X,y∈YP(x,y)[logP(y|x)+logP(x)]=−∑x∈X,y∈YP(x,y)logP(y|x)+[−∑x∈XP(x)logP(x)]=H(Y|X)+H(x) H ( X , Y ) = − ∑ x ∈ X , y ∈ Y P ( x , y ) log P ( x , y ) = − ∑ x ∈ X , y ∈ Y P ( x , y ) log [ P ( y | x ) P ( x ) ] = − ∑ x ∈ X , y ∈ Y P ( x , y ) [ log P ( y | x ) + log P ( x ) ] = − ∑ x ∈ X , y ∈ Y P ( x , y ) log P ( y | x ) + [ − ∑ x ∈ X P ( x ) log P ( x ) ] = H ( Y | X ) + H ( x )
proof: H(X,Y|Z)=H(X|Z)+H(Y|X,Z) H ( X , Y | Z ) = H ( X | Z ) + H ( Y | X , Z )
H(X,Y|Z)=−∑x,y,zP(x,y,z)logP(x,y|z)=−∑x,y,zP(x,y,z)log[P(x,y,z)P(z)]=−∑x,y,zP(x,y,z)log[P(x,y,z)P(x,z)P(x,z)p(z)]=[−∑x,y,zP(x,y,z)logP(x,y,z)P(x,z)]+[−∑x,y,zP(x,y,z)logP(x,z)P(z)]=[−∑x,y,zP(x,y,z)logP(x,y,z)P(x,z)]+[−∑x,zP(x,z)logP(x,z)P(z)]=H(Y|X,Z)+H(X|Z) H ( X , Y | Z ) = − ∑ x , y , z P ( x , y , z ) log P ( x , y | z ) = − ∑ x , y , z P ( x , y , z ) log [ P ( x , y , z ) P ( z ) ] = − ∑ x , y , z P ( x , y , z ) log [ P ( x , y , z ) P ( x , z ) P ( x , z ) p ( z ) ] = [ − ∑ x , y , z P ( x , y , z ) log P ( x , y , z ) P ( x , z ) ] + [ − ∑ x , y , z P ( x , y , z ) log P ( x , z ) P ( z ) ] = [ − ∑ x , y , z P ( x , y , z ) log P ( x , y , z ) P ( x , z ) ] + [ − ∑ x , z P ( x , z ) log P ( x , z ) P ( z ) ] = H ( Y | X , Z ) + H ( X | Z )
相对熵(KL-散度)
DKL(P∣∣Q)=∑x∈XP(x)logP(x)Q(x)=Ex∼P[logP(x)Q(x)]=Ex∼P[logP(x)−logQ(x)] D K L ( P ∣∣ Q ) = ∑ x ∈ X P ( x ) log P ( x ) Q ( x ) = E x ∼ P [ log P ( x ) Q ( x ) ] = E x ∼ P [ log P ( x ) − log Q ( x ) ]
note:DKL(P∣∣Q)≥0 D K L ( P ∣∣ Q ) ≥ 0 ,用于衡量两个分布的相似性
交叉熵
H(P,Q)=H(P)+DKL(P∣∣Q)H(P,Q)=−Ex∼PlogQ(x) H ( P , Q ) = H ( P ) + D K L ( P ∣∣ Q ) H ( P , Q ) = − E x ∼ P log Q ( x )
边缘概率,条件概率,联合概率
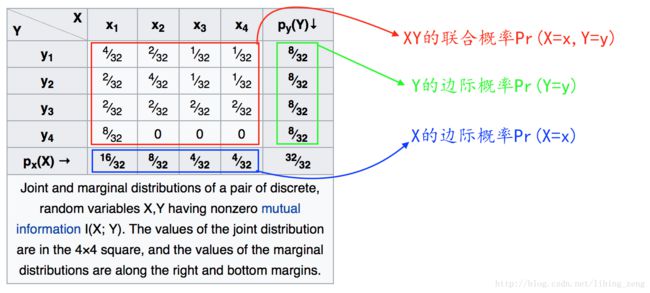
- 边缘概率就是计算每一边
- 联合概率计算的是 P(X=x,Y=y)=P(y|x)P(x) P ( X = x , Y = y ) = P ( y | x ) P ( x )
- 条件概率计算的是 P(y|x)=P(x,y)P(x) P ( y | x ) = P ( x , y ) P ( x )
example
H(X)=−∑x∈XP(x)logp(x)=12log2+14log4+18log8+18log8=74log2=74bits H ( X ) = − ∑ x ∈ X P ( x ) log p ( x ) = 1 2 log 2 + 1 4 log 4 + 1 8 log 8 + 1 8 log 8 = 7 4 log 2 = 7 4 b i t s
H(X|Y)=−∑x∈Xy∈YP(x,y)logP(x,y)P(y)=432log1/44/32+232log1/42/32+232log1/42/32+⋅⋅⋅=118bits H ( X | Y ) = − ∑ x ∈ X y ∈ Y P ( x , y ) l o g P ( x , y ) P ( y ) = 4 32 log 1 / 4 4 / 32 + 2 32 log 1 / 4 2 / 32 + 2 32 log 1 / 4 2 / 32 + ⋅ ⋅ ⋅ = 11 8 b i t s
H(X,Y)=−∑x∈Xy∈YP(x,y)logP(x,y)=278bits H ( X , Y ) = − ∑ x ∈ X y ∈ Y P ( x , y ) l o g P ( x , y ) = 27 8 b i t s