SPP-net论文学习

这篇是目标检测一系列论文中的第二篇，第一作者是发明ResNet的何凯明。

论文地址：https://arxiv.org/pdf/1406.4729.pdf
本博客参考了前辈v1_vivian的博文：https://blog.csdn.net/v1_vivian/article/details/73275259

Abstract

之前的CNNs都需要一个固定大小的输入图像，这就会损害对任意大小图像的识别准确度。在这篇论文里，作者提出了一个新的池化方法 — “Spatial pyramid pooling”（金字塔池化），以解决上述问题。新的网络被称作SPP-net，不管图像输入的大小，它都能产生一个固定长度的输出。Pyramid pooling对变形了的目标也很鲁棒。因此，SPP-net能有效提升所有的基于CNN的图像分类算法。在ImageNet 2012, Pascal VOC 2007, Caltech 101 等数据集上，SPP-net都表现不俗。

在目标检测上SPP-net也很有用。通过SPP-net，只需要计算整张图的特征映射一次，然后在任意区域中pool特征，生成固定长度的输出给检测器去训练。这样避免了重复计算卷积特征。在测试图像上获得相同准确性的情况下，此方法比R-CNN快24-102倍。
在ImageNet Large Scale Visual Recognition Challenge (ILSVRC) 2014数据集上，此方法在目标检测排名第二，在图像分类排名第三。

1. Introduction

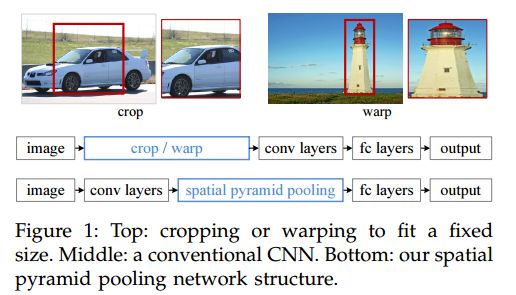
之前的方法都需要固定长度的输入图像，比如224 $\times$ 224，当输入图像是任意时，它们就需要裁剪或扭曲图像以满足固定输入的要求。但是裁剪下的区域可能只是对象的一部分，扭曲也会损害图像的几何结构。这都会损害图像识别的准确度。
那么为什么CNN一定需要固定长度的输入呢？CNN主要包含两个部分，卷积层和全连接层。卷积层通过操作一个滑动窗口来输出能代表图像空间分布的特征图。但是卷积层并不需要一个固定长度的输入，它能产生任意大小的特征图。另一方面，全连接层却需要固定长度的输入，因为它要把输入的所有像素点连接起来,需要指定输入层神经元个数和输出层神经元个数，所以需要规定输入的feature的大小。
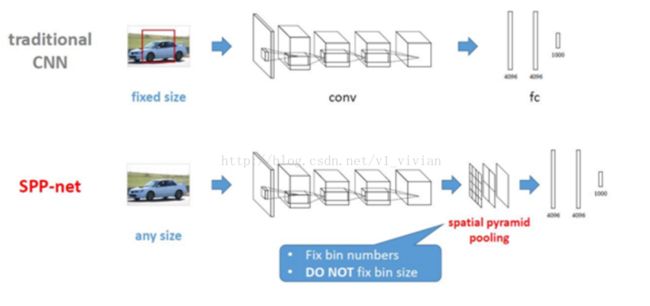
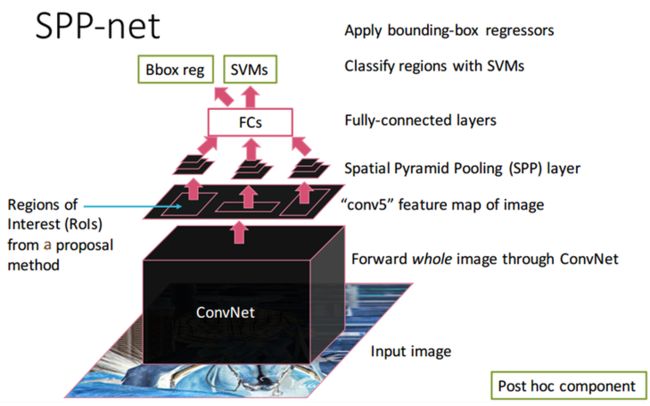
因此这篇论文提出的Spatial pyramid pooling（空间金字塔池化）层来去除那个束缚，作者在最后一个卷积层上增加一个SPP层。SPP层池化特征，生成固定长度的输出，然后这些输出被导入全连接层。这样，通过“聚合”卷积层和全连接层之间的信息，就不需要再去裁剪和扭曲图像。下图是两个网络的对比：

SPP按从优到次等级将图像分为若干个部分，然后聚合局部特征。在CNN称霸之前的分类和检测竞赛中，SPP都是算法赢得比赛的关键组成部分。但是至今想到过在CNN中加入SPP，作者发现在CNN中加入SPP会有以下特性：

• 不管输入的大小，SPP能够产生固定长度输出，但是CNN中滑动窗口池化不行；
• SPP 利用multi-level spatial bins，但是滑动窗口池化只有一个窗口；
• SPP能池化由不同的scale上产生的特征，因为它输入size很灵活。

用不同大小的图像来训练能够提升scale-invariance（大小不变性），并降低过拟合。针对不同的输入大小，作者想出了一个简单的训练方法。让一个网络去接受不同大小的输入，可以近似地看作我们有多个共享参数的网络，然后每一个网络用给定大小的输入去训练。在每次训练迭代中，向网络中输入一个给定大小的输入，然后在下一次迭代中，再向网络中输入另一个大小的输入。实验表明与单一size的训练相比，multi-size的训练收敛，而且测试准确性更高。

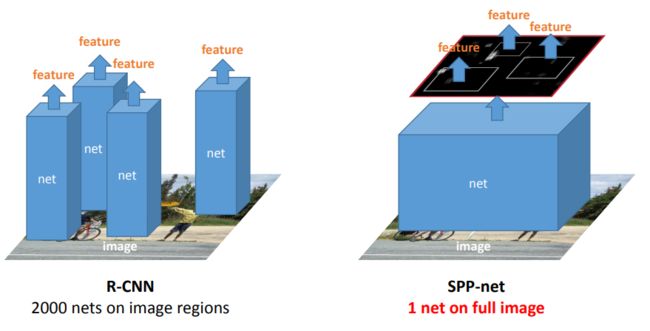
在R-CNN中，特征计算很费时间，因为在每张图像的warped region上它都会重复使用卷积网络。而在这篇论文中，作者提出只需在整张图像上应用一次卷积网络，然后用SPP-net在特征图上提取特征。这就比R-CNN快接近一百倍。结合快速proposal方法EdgeBoxes, 此方法只需要0.5秒就能处理一张图片。

2. Deep networks with spatial pyramid pooling

2.1 Convolution layers and feature maps

在CNN中，卷积层后会跟着池化层，这些池化层也可以被认为是卷积，因为它们也利用滑动窗口。最后是全连接层，N-way softmax作为输出，N是类别的个数。

深度网络需要固定长度的输入，但是这一要求仅仅是因为全连接层需要。而卷积层可以给定任意长度的输入。卷积层使用滑动滤波器，输出与输入有着几乎一致的长宽比。这些输出称作feature map. 以下是$con{v}_5$层生成的特征图的可视化：

从图2中可看出，特征图的生成不需要固定长度的输入。这与传统方法的特征图类似，传统方法是然后将这些特征通过Bag of words或Spatial pyramids进行池化。

2.2 The spatial pyramid pooling layers

卷积层接受任意的输入大小，但是输出的大小不是固定的。而且分类器（SVM/softmax）是需要固定长度的输入向量。Spatial pyramid pooling 改进了bag of words，因为它通过在local spatial bin中池化，以保持空间信息。这些bin与图像大小是成比例的，所以bin的个数是固定的。这就和滑动窗口不同，滑动窗口的个数取决于输入的大小。
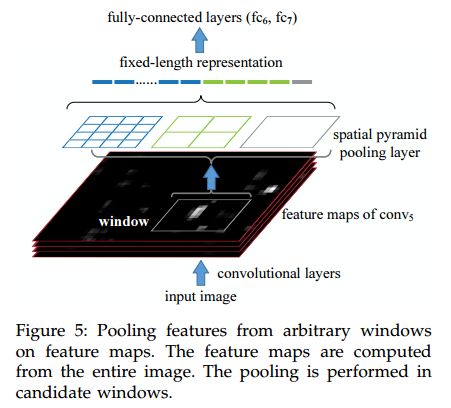
因此，作者替换了最后一个池化层$poo{l}_5$为spatial pyramid pooling层。下图为方法的介绍：

在每一个bin，都用max-pool池化每个滤波器的response。这样，SPP的输出就是kM维度，M是bin的个数，k是滤波器的个数。固定维度的向量作为全连接层的输出。这样，输入可以是任意的大小。图中输出大小为$(16+4+1)\times 256$。

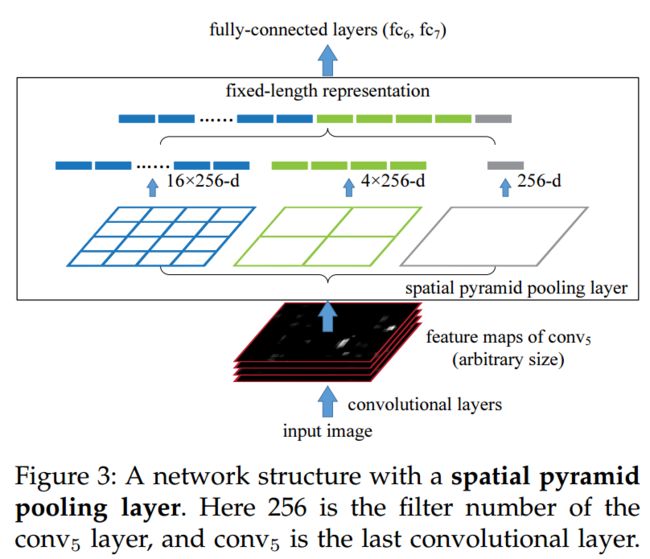
以下图为例：

黑色图片代表卷积之后的特征图，接着我们以不同大小的块来提取特征，分别是44，22，1*1，将这三张网格放到下面这张特征图上，就可以得到16+4+1=21种不同的块(Spatial bins)，我们从这21个块中，每个块提取出一个特征，这样刚好就是我们要提取的21维特征向量。这种以不同的大小格子的组合方式来池化的过程就是空间金字塔池化（SPP）。比如，要进行空间金字塔最大池化，其实就是从这21个图片块中，分别计算每个块的最大值，从而得到一个输出单元，最终得到一个21维特征的输出。

2.3 Training network

理论上，上述的网络可以通过标准的反向传播来训练，不用管输入的大小。但实际上，caffe等实现中，为了计算的方便，GPU，CUDA等比较适合固定尺寸的输入，所以训练的时候输入是固定了尺度了的。
论文中将网络的训练分为两种：一种是single-size,一种是Multi-size。

Single-size training

首先考虑网络接受一个固定大小输入的情况，需要从原图片中做裁剪。裁剪的目的在于数据增广。如果给定了图片的大小，我们可以提前计算SPP所需bin的大小。假设$con{v}_5$输出的特征图大小是$a\times a$，pyramid level有$n\times n$个bin。这就是滑动窗口池化，窗口大小为$win=\lceil a/n\rceil$，stride是$str=\lfloor a/n\rfloor$. 对于$l$-level pyramid，我们有$l$个这样的层。然后全连接层把这$l$个输出串在一起。

对于pool $3\times 3$: sizeX=5 的计算公式是：$\lceil 13/3\rceil =5$ ，stride = 4的计算公式是：$\lfloor 13/3\rfloor =4$。
如果输入改成$180\times 180$，这时候conv5出来的reponse map为$10\times 10$，类似的方法，能够得到新的pooling参数。

Multi-size training

为了能输入不同大小的图像，使用两个尺度来训练，$180\times 180$，$224\times 224$。

训练的时候，$224\times 224$的图片通过crop得到，$180\times 180$的图片通过缩放$224\times 224$的图片得到。之后，迭代训练，即用224的图片训练一个epoch，之后180的图片训练一个epoch，交替地进行。

这样不同大小的图片只有分辨率的差异，而不存在内容或布局的差异。两种尺度下，在SSP后，输出的特征维度都是(9+4+1)x256，参数是共享的，之后接全连接层即可。这样在训练中，我们就通过两个固定大小且共享参数的网络来实现了一个输入大小可变的SPP-net。论文中说，这样训练的好处是可以更快的收敛。

以上single-size和multi-size只是针对训练时候用，在测试阶段，SPP-net的输入是任意大小的。

3.Comparison between SPP-net and R-CNN

• 对于R-CNN，整个过程是：

1. 首先通过选择性搜索，对待检测的图片进行搜索出~2000个候选窗口。
2. 把这2k个候选窗口的图片都缩放到$227\times 227$，然后分别输入CNN中，每个proposal提取出一个特征向量，也就是说利用CNN对每个proposal进行提取特征向量。
3. 把上面每个候选窗口的对应特征向量，利用SVM算法进行分类识别。

可以看出R-CNN的计算量是非常大的，因为2k个候选窗口都要输入到CNN中，分别进行特征提取。

• 对于SPP-Net，整个过程是：

1. 首先通过选择性搜索，对待检测的图片进行搜索出2000个候选窗口。这一步和R-CNN一样。
2. 特征提取阶段。这一步就是和R-CNN最大的区别了，这一步骤的具体操作如下：把整张待检测的图片，输入CNN中，进行一次性特征提取，得到feature maps，然后在feature maps中找到各个候选框的区域，再对各个候选框采用金字塔空间池化，提取出固定长度的特征向量。而R-CNN是直接提取image region，然后在进入CNN，因为SPP-Net只需要一次对整张图片进行特征提取，速度会大大提升。
3. 最后一步也是和R-CNN一样，采用SVM算法进行特征向量分类识别。

Mapping a window to feature maps

我们知道，在原图中的proposal,经过多层卷积之后，位置还是相对于原图不变的（如下图所示），那现在需要解决的问题就是，如何能够将原图上的proposal,映射到卷积之后得到的特征图上，因为在此之后我们要对proposal进行金字塔池化。

对于映射关系，论文中给出了一个公式：

假设$(x^{\prime },y^{\prime })$表示特征图上的坐标点，坐标点$(x,y)$表示原输入图片上的点，那么它们之间有如下转换关系，这种映射关心与网络结构有关：$(x,y)=(S\times x^{\prime },S\ast y^{\prime })$

反过来，我们希望通过$(x,y)$坐标求解$(x^{\prime },y^{\prime })$，那么计算公式如下：
$$x^{\prime }=\lfloor x/S\rfloor +1,(left-top)$$
$$x^{\prime }=\lceil x/S\rceil -1,(right-bottom)$$
其中S就是CNN中所有的strides的乘积，包含了池化、卷积的stride。

论文中使用的是 ZF-5：$S=2\times 2\times 2\times 2=16$
Overfeat-5/7 : $S=2\times 3\times 2=12.$

Object detection

对于检测算法，论文中是这样做到：使用"fast" mode of selective search生成约2000个候选框，缩放图像$min(w,h)=s$之后提取特征，每个候选框使用一个4层的空间金字塔池化特征，网络使用的是ZF-5的SPP-Net形式。之后将12800维的特征输入全连接层，binary linear SVM的输入为全连接层的输出。

这个算法可以应用到多尺度的特征提取：先将图片resize到五个尺度：480，576，688，864，1200，加自己6个。然后在map window to feature map一步中，选择ROI框尺度在｛6个尺度｝中大小最接近$224\times 224$的那个尺度下的feature maps中提取对应的ROI feature。这样做可以提高系统的准确率。

4. Conclusion

SPPnet总体流程如下图所示：