再谈LCA:倍增与Tarjan
LCA,不认识的戳这里。
接下来我们就可以谈谈解决这个的方法。
具体方法有:暴力求LCA,倍增求LCA,Tarjan离线求LCA,ST求LCA。
The first : 暴力
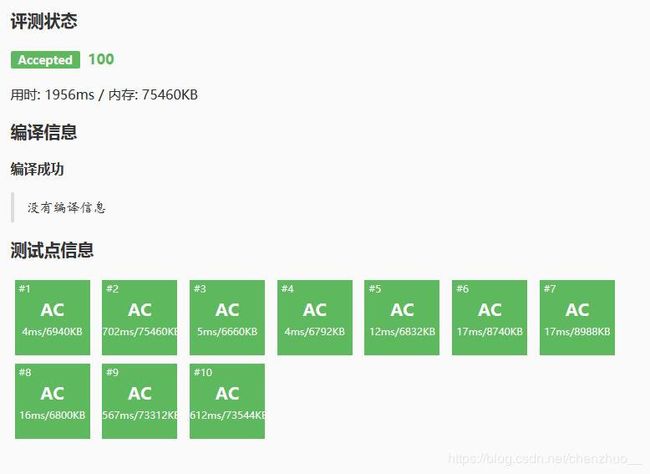
所谓暴力求LCA,就是说给我们两个点,我们就沿着到根的路径一步一步往上走,之后再从另一个一点一点往上走,首先相碰的点即为所求LCA。但是从描述上我们就可以看出,这样子的代码时间复杂度极高。因此很容易T飞,拿我在洛谷的模板LCA的评测结果说话:
所以说还是别用这种方法的好。不过代码还是可以奉上的(还是不懂就看注释):
#include
using namespace std;
int dis[1050001],fa[1050001],head[1050001],vis[1050001],n,m,root,tot;
struct node{
int to,next;
}e[1050001];
inline void add(int x,int y){
e[++tot].to=y;
e[tot].next=head[x];
head[x]=tot;
}
inline void dfs(int x){
vis[x]=1;//标记为已走过
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(vis[y])continue;//走过就跳过,不然会死循环,因为是双向边
fa[y]=x;//将y的祖先定义为x
dfs(y);//从y开始往下搜
}
}
inline void find(int x,int fath){
dis[x]=dis[fath]+1;//不写加一也没关系,加一可以具体看深度,主要是为了标记
if(fa[x]==0)return;//随便加的,避免bomb
find(fa[x],x);//继续往下找
}
int main(){
scanf("%d%d%d",&n,&m,&root);//详情参考https://www.luogu.org/problemnew/show/P3379的题目读入
//懒得人看这边 :读入是点数,边数,根
for(int i=0;++i emmm那就这样了。毕竟主讲不在这里。。。
The second : 倍增
倍增求LCA其实蛮好理解的。。。这里尝试让大家理解一下。。。
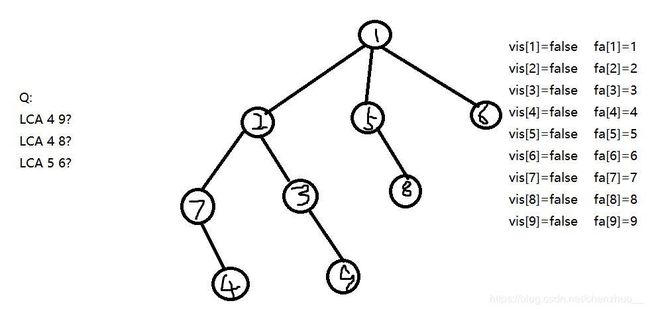
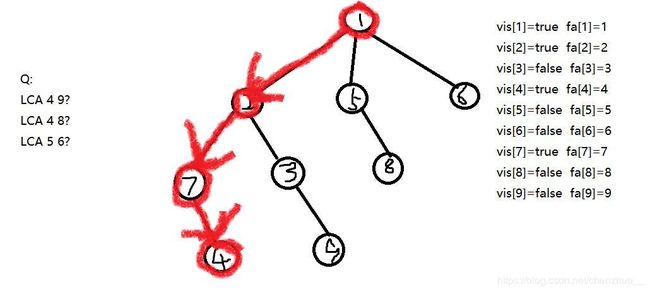
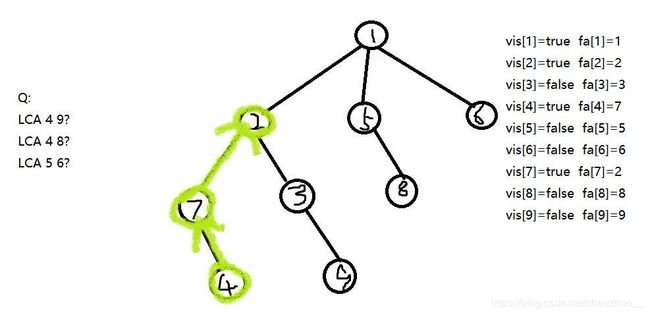
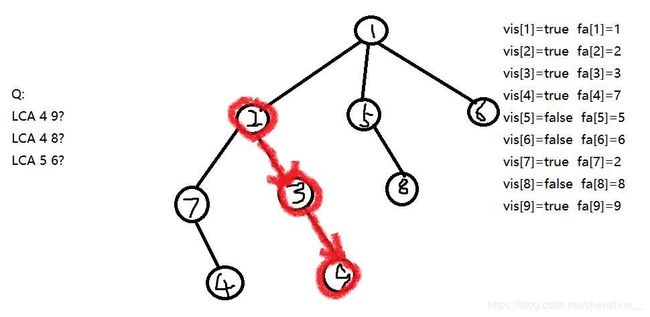
我们现在看看2这个数字的神奇所在,当一个序列有1,2,4,8,16,32……这些数后,你便拥有了整个数字王国--没有一个数字你无法组合出来。所以我们便可以考虑预处理出一个节点的二的整次幂的父亲。但是这个怎么做到呢?我们先用fa[x][i]表示x的(1< fa[x][i]=fa[ fa [ x ] [ i-1 ] ] [ i-1 ],yes以上就是……初始化的过程?!下帖代码: 求出这个东西之后,你便可以随便的穿梭于一个节点的祖先之中。。。 初始化完了,也就应该考虑考虑主程序了。。。怎么做呢? 给出一幅图: fa[x][0]即可,这里会有人问:为什么要输出这个?我们捡起刚才的栗子,13现在跳到12了,12要和6找到最近的祖先,怎么办?首先找到12最远可以跳到fa[12][2],即为他的爷爷的爷爷,6也是如此,这样一跳,便直接碰到了,但是会不会有更低的LCA呢? 我们还是得找,所以这步我们不跳,接下来12便要去爷爷家做客,6也要去,于是它们两没碰到,但它们不灰心,因为迟早会碰到的─=≡Σ(((つ•̀ω•́)つ。现在12到了3,6到了2,还得跳啊!3要往上跳1,2也是,它们会碰到,所以还是得考虑先不跳,等待最优解,于是它们没得跳了,这……碰不找了?∑(っ°Д°;)っ,没有关系,最后输出的fa[3][0]使3华丽上跳,一跃越到了LCA!这便是最后的作用,它相当于……问个问题,给你个8,让你用小于8的2的整次幂(每个数只准用一次)以及2个1怎么做到?答案就摆在这里啊:8=1+2+4+1,这个1便是源于最后的增加,它可以使你放心的往上跳,而不用怕错过LCA,真是神奇! 下面就是代码时间: 所以这一块就解决了?那我就当你们解决了哈。 The third : Tarjan 这便是我最先理解的算法(其实是先会写的方法)。这个算法不同于前面介绍的倍增,这个算法是一种离线算法,也就是要等读入读完一次性做。具体做法:我们先从根节点进行一次深度优先遍历,当遍历到一个点的时候,将其的所有子节点的祖先都定义为自身,在其将要回溯之前,将所有与这个点有关的询问都做掉,具体做法:将询问建成一张无向图,将与这个点有关的询问都进行一遍判断:若当前询问的另一个点已经访问过,那么LCA便是另一个点能追溯到的最远祖先。我觉得我需要再给你们 一开始的状态,我们现在开始往下做,先遍历,于是: 发现与4有关的询问9并未被更新过,于是我们忽略它,便有了回溯: 于是乎4,7的祖先现在都改变了,接下来继续往下: 接下来便有了好戏:与9有关的询问有4,而4恰好被访问过了!因此我们就可以大胆的回答这组询问,但是这次查询的不是9的祖先而是4的祖先,于是便有了LCA(4,9)=2,这就找到了。是不是很神奇呢?( 好了,上承代码: 两者跑洛谷的模板LCA的情况: 以上就是LCA的两种计算方法了。。。 坑总算填上了。。。 推荐几道题: 模板LCA 依旧是……说不出FA 稍作处理的一道LCA*题 海星 第一题题解博客传送门:here 第四题题解博客传送门:go emmmm 就到这里吧! 谢谢观赏。 inline void dfs(int x,int father){
deep[x]=deep[father]+1;//预处理每个节点的深度deep
fa[x][0]=father;//预处理每个节点的祖先
for(int i=0;++i<=25;)
fa[x][i]=fa[fa[x][i-1]][i-1];//利用所推关系式方便的处理出一个节点的整次幂祖先,是不是很棒?
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y!=father)dfs(y,x);
}
}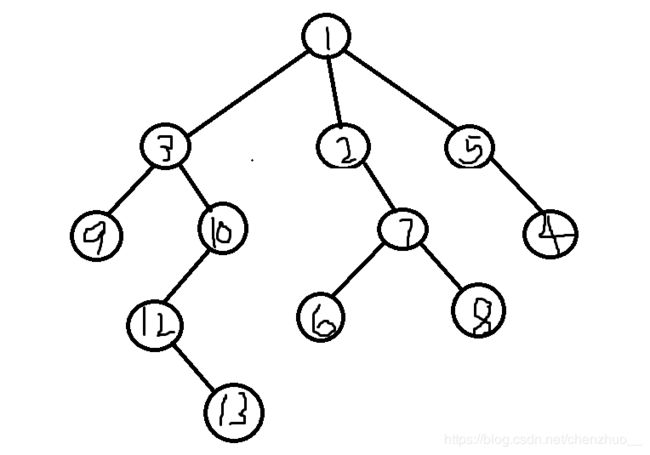
此图巨丑不要在意,for example:我们找找13和6的最近公共祖先,显然,它们现在不在一个深度,那么怎么办?我们先让深度深的作为x,浅的作为y,然后先让x跳到与y为同一起跑线。之后怎么做呢?之后其实很简单了,有了初始化为我们打下半壁江山,我们只需要让这两个节点飞一般的往上跳就好了。不过这里要注意从大往小跳,为什么呢?从大往小,不可能超过你最远跳跃距离,因为超过就会取消本次机次。但是从小跳,你可能会有一些点到不了,就会多出回溯之类的东东。好,现在我们按照这个方法跳,从大往小跳,每次往上跳后,判断是否到了同一节点,不是就继续减小幅度跳,这样就可以找到LCA,最后输出inline int LCA(int x,int y){
if(deep[x]洗个脑。这次搞个小点的图。突然发现这个解释起来有点。。。)
//Tarjan
#include
//±¶Ôö
#include 好了,如果你刷完了这些题,你就算是对LCA有一些初步了解了。(当然,如果你是个dalao,但是你没刷过这些题,就当没看见这句话)