洛谷试炼场之简单的模拟

 P1003 铺地毯

• • 25.1K通过
  • 62K提交
• 题目提供者CCF_NOI
• 评测方式云端评测
• 标签NOIp提高组2011
• 难度普及-
• 时空限制1000ms / 128MB

 提交  题解   

• 提示：收藏到任务计划后，可在首页查看。

最新讨论显示

推荐的相关题目显示

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 nn 张地毯，编号从 11 到nn。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入输出格式

输入格式：

 

输入共n+2n+2行

第一行，一个整数nn，表示总共有nn张地毯

接下来的nn行中，第 i+1i+1行表示编号ii的地毯的信息，包含四个正整数a ,b ,g ,ka,b,g,k ，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标(a,b)(a,b)以及地毯在xx轴和yy轴方向的长度

第n+2n+2行包含两个正整数xx和yy，表示所求的地面的点的坐标(x,y)(x,y)

 

输出格式：

 

输出共11行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1−1

 

输入输出样例

输入样例#1： 复制

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

输出样例#1： 复制

3

输入样例#2： 复制

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

输出样例#2： 复制

-1

说明

【样例解释1】

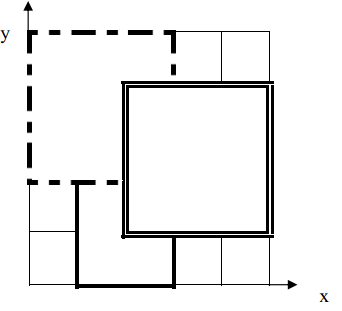
如下图，11 号地毯用实线表示，22 号地毯用虚线表示，33 号用双实线表示，覆盖点(2,2)(2,2)的最上面一张地毯是 33号地毯。

【数据范围】

对于30% 的数据，有 n ≤2n≤2 ；
对于50% 的数据，0 ≤a, b, g, k≤1000≤a,b,g,k≤100；
对于100%的数据，有 0 ≤n ≤10,0000≤n≤10,000 ，0≤a, b, g, k ≤100,0000≤a,b,g,k≤100,000。

noip2011提高组day1第1题

代码：

//#pragma GCC optimize ("O3")
#include
using namespace std;
const int maxn = (int)1e4 + 10;
struct node
{
    int a,b,g,k;
}p[maxn];
int main()
{
    int n;
    scanf("%d",&n);
    int x,y;
    for (int i = 1;i <= n;i ++)
    {
        scanf("%d %d %d %d",&p[i].a,&p[i].b,&p[i].g,&p[i].k);
    }
    scanf("%d %d",&x,&y);
    int ans = -1;
    for (int i = 1;i <= n;i ++)
    {
        if (p[i].a <= x && p[i].a + p[i].g >= x && p[i].b <= y && p[i].k + p[i].b >= y)
            ans = i;
    }
    printf("%d\n",ans);
    return 0;
}

P1067 多项式输出

• • 13K通过
  • 44.8K提交
• 题目提供者CCF_NOI
• 评测方式云端评测
• 标签NOIp普及组2009
• 难度普及-
• 时空限制1000ms / 128MB

 提交  题解   

• 提示：收藏到任务计划后，可在首页查看。

最新讨论显示

推荐的相关题目显示

题目描述

一元nn次多项式可用如下的表达式表示：

其中，a_ix^iai​xi称为ii次项，a_iai​ 称为ii次项的系数。给出一个一元多项式各项的次数和系数，请按照如下规定的格式要求输出该多项式：

1. 多项式中自变量为xx，从左到右按照次数递减顺序给出多项式。

2. 多项式中只包含系数不为00的项。

3. 如果多项式nn次项系数为正，则多项式开头不出现“++”号，如果多项式nn次项系

数为负，则多项式以“-−”号开头。

4. 对于不是最高次的项，以“++”号或者“-−”号连接此项与前一项，分别表示此项

系数为正或者系数为负。紧跟一个正整数，表示此项系数的绝对值（如果一个高于00次的项，

其系数的绝对值为11，则无需输出 11）。如果xx的指数大于11，则接下来紧跟的指数部分的形

式为“x^bxb”，其中 bb为 xx的指数；如果 xx的指数为11，则接下来紧跟的指数部分形式为“xx”；

如果 xx 的指数为00，则仅需输出系数即可。

5. 多项式中，多项式的开头、结尾不含多余的空格。

输入输出格式

输入格式：

 

输入共有 22 行

第一行11 个整数，nn，表示一元多项式的次数。

第二行有 n+1n+1个整数，其中第ii个整数表示第n-i+1n−i+1 次项的系数，每两个整数之间用空格隔开。

 

输出格式：

 

输出共 11 行，按题目所述格式输出多项式。

 

输入输出样例

输入样例#1： 复制

5 
100 -1 1 -3 0 10

输出样例#1： 复制

100x^5-x^4+x^3-3x^2+10

输入样例#2： 复制

3 
-50 0 0 1 

输出样例#2： 复制

-50x^3+1 

说明

NOIP 2009 普及组 第一题

对于100%数据，0 \le n \le 1000≤n≤100,-100 \le−100≤系数\le 100≤100

思路：

果然模拟题（洛谷）都挺恶心的，这个题坑点其实挺多的，简单列举一下

1、系数为0不必输出（可能会认为全为0就输出0，测试点2我估计就是这个）

2、如果第一个系数（包括3 0 0 0 1这样的测试数据，即第一个输出的系数为正数就不用输出+）是正数不能输出+

3、最后一个系数即常数要输出

4、系数为1或-1只需输出正负号即可，但如果这个数是最后一个系数即常数要输出

我遇到的差不多就这几个了

代码：

#pragma GCC optimize ("O3")
#include
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    n ++;
    int x;
    bool flag = 0;
    while (n --)
    {
        scanf("%d",&x);
//        if (!x && !n)
//            putchar('0');刚开始就当成了全为0要有输出
        if (!x)
            continue;
        if (x == -1 && n)
            putchar('-');
        else if (x > 0)
        {
            if (flag)
                putchar('+');
            if (x != 1 || !n)
                printf("%d",x);

        }
        else
            printf("%d",x);
        flag = 1;
        if (n > 1)
            printf("x^%d",n);
        else if (n == 1)
            putchar('x');
    }
    putchar('\n');
    return 0;
}

P1540机器翻译

题目背景

小晨的电脑上安装了一个机器翻译软件，他经常用这个软件来翻译英语文章。

题目描述

这个翻译软件的原理很简单，它只是从头到尾，依次将每个英文单词用对应的中文含义来替换。对于每个英文单词，软件会先在内存中查找这个单词的中文含义，如果内存中有，软件就会用它进行翻译；如果内存中没有，软件就会在外存中的词典内查找，查出单词的中文含义然后翻译，并将这个单词和译义放入内存，以备后续的查找和翻译。

假设内存中有MM个单元，每单元能存放一个单词和译义。每当软件将一个新单词存入内存前，如果当前内存中已存入的单词数不超过M-1M−1，软件会将新单词存入一个未使用的内存单元；若内存中已存入MM个单词，软件会清空最早进入内存的那个单词，腾出单元来，存放新单词。

假设一篇英语文章的长度为NN个单词。给定这篇待译文章，翻译软件需要去外存查找多少次词典？假设在翻译开始前，内存中没有任何单词。

输入输出格式

输入格式：

 

共22行。每行中两个数之间用一个空格隔开。

第一行为两个正整数M,NM,N，代表内存容量和文章的长度。

第二行为NN个非负整数，按照文章的顺序，每个数（大小不超过10001000）代表一个英文单词。文章中两个单词是同一个单词，当且仅当它们对应的非负整数相同。

 

输出格式：

 

一个整数，为软件需要查词典的次数。

 

输入输出样例

输入样例#1： 复制

3 7
1 2 1 5 4 4 1

输出样例#1： 复制

5

说明

每个测试点1s1s

对于10\%10%的数据有M=1,N≤5M=1,N≤5。

对于100\%100%的数据有0≤M≤100,0≤N≤10000≤M≤100,0≤N≤1000。

整个查字典过程如下：每行表示一个单词的翻译，冒号前为本次翻译后的内存状况：

空：内存初始状态为空。

1．11：查找单词1并调入内存。

2． 1 212：查找单词22并调入内存。

3． 1 212：在内存中找到单词11。

4． 1 2 5125：查找单词55并调入内存。

5． 2 5 4254：查找单词44并调入内存替代单词11。

6．2 5 4254：在内存中找到单词44。

7．5 4 1541：查找单词1并调入内存替代单词22。

共计查了55次词典。

思路：

模拟，想了一些STL还是直接模拟更好一些

代码：

#pragma GCC optimize ("O3")
#include
using namespace std;
#define inf 0x3f3f3f3f
int word[1010];
bool vis[1010];
int main()
{
    int m,n;
    scanf("%d %d",&m,&n);
    for (int i = 1;i <= n;i ++)
        scanf("%d",&word[i]);
    int ans = 0,l = 1;
    for (int i = 1;i <= n;i ++)
    {
        if (!vis[word[i]])
        {
            ans ++;
            vis[word[i]] = 1;
            if (ans > m)
            {
                vis[word[l]] = 0;
                l ++;
                while (word[l] == inf)
                    l ++;
            }
        }
        else
            word[i] = inf;//已经在词典中的标记一下防止更替时出错
    }
    printf("%d\n",ans);
    return 0;
}

P1056排座椅

题目描述

上课的时候总会有一些同学和前后左右的人交头接耳，这是令小学班主任十分头疼的一件事情。不过，班主任小雪发现了一些有趣的现象，当同学们的座次确定下来之后，只有有限的D对同学上课时会交头接耳。

同学们在教室中坐成了MM行NN列，坐在第i行第j列的同学的位置是(i,j)(i,j)，为了方便同学们进出，在教室中设置了KK条横向的通道，LL条纵向的通道。

于是，聪明的小雪想到了一个办法，或许可以减少上课时学生交头接耳的问题：她打算重新摆放桌椅，改变同学们桌椅间通道的位置，因为如果一条通道隔开了22个会交头接耳的同学，那么他们就不会交头接耳了。

请你帮忙给小雪编写一个程序，给出最好的通道划分方案。在该方案下，上课时交头接耳的学生的对数最少。

输入输出格式

输入格式：

 

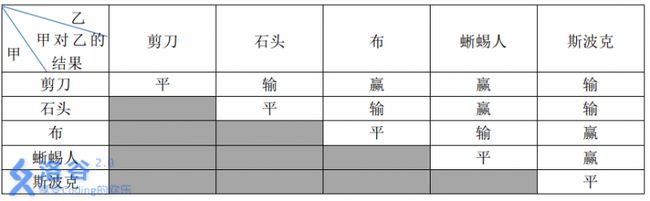
第一行，有55个用空格隔开的整数，分别是M,N,K,L,D(2 \le N,M \le 1000,0 \le K

接下来的DD行，每行有44个用空格隔开的整数。第ii行的44个整数X_i,Y_i,P_i,Q_iXi​,Yi​,Pi​,Qi​，表示坐在位置(X_i,Y_i)(Xi​,Yi​)与(P_i,Q_i)(Pi​,Qi​)的两个同学会交头接耳（输入保证他们前后相邻或者左右相邻）。

输入数据保证最优方案的唯一性。

 

输出格式：

 

共两行。
第一行包含KK个整数a_1,a_2,…,a_Ka1​,a2​,…,aK​，表示第a_1a1​行和a_1+1a1​+1行之间、第a-2a−2行和a_2+1a2​+1行之间、…、第a_KaK​行和第a_K+1aK​+1行之间要开辟通道，其中a_i< a_i+1ai​

第二行包含LL个整数b_1,b_2,…,b_Lb1​,b2​,…,bL​，表示第b_1b1​列和b_1+1b1​+1列之间、第b_2b2​列和b_2+1b2​+1列之间、…、第b_LbL​列和第b_L+1bL​+1列之间要开辟通道，其中b_i< b_i+1bi​

 

输入输出样例

输入样例#1： 复制

4 5 1 2 3
4 2 4 3
2 3 3 3
2 5 2 4

输出样例#1： 复制

2
2 4

说明

上图中用符号*、※、+标出了33对会交头接耳的学生的位置，图中33条粗线的位置表示通道，图示的通道划分方案是唯一的最佳方案。

2008年普及组第二题

思路：

麻烦的模拟，注意输出的坐标也是要排好序的

代码：

#include
using namespace std;
const int maxn = (int)1e3 + 10;
int dx[maxn],dy[maxn];
struct node
{
    int x,crd;
}dif[maxn];
bool cmp(node a,node b)
{
    return a.x > b.x;
}
int main()
{
    memset(dx,0,sizeof(dx));
    memset(dy,0,sizeof(dy));
    int m,n,k,l,d;
    scanf("%d %d %d %d %d",&m,&n,&k,&l,&d);
    int x1,y1,x2,y2;
    while (d--)
    {
        scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
        if (x1 == x2)
            dy[min(y1,y2)] ++;
        else
            dx[min(x1,x2)] ++;
    }
    int p = 0;
    for (int i = 1;i < m;i ++)
    {
        if (dx[i])
            dif[p].x = dx[i],dif[p ++].crd = i;
    }
    sort(dif,dif + p,cmp);
    int pos = 0;
    for (int i = 0;i < k;i ++)
        dx[i] = dif[i].crd;
    sort(dx,dx + k);
    bool flag = 0;
    for (int i = 0;i < k;i ++)
    {
        if (flag)
            putchar(' ');
        flag = 1;
        printf("%d",dx[i]);
    }
    putchar('\n');
    p = flag = 0;
    for (int i = 1;i < n;i ++)
    {
        if (dy[i])
            dif[p].x = dy[i],dif[p++].crd = i;
    }
    sort(dif,dif + p,cmp);
    for (int i = 0;i < l;i ++)
        dx[i] = dif[i].crd;
    sort(dx,dx + l);
    for (int i = 0;i < l;i ++)
    {
        if (flag)
            putchar(' ');
        flag = 1;
        printf("%d",dx[i]);
    }
    putchar('\n');
    return 0;
}

P1328 生活大爆炸版石头剪刀布

• • 11.2K通过
  • 18.8K提交
• 题目提供者CCF_NOI
• 评测方式云端评测
• 标签NOIp提高组2014
• 难度普及-
• 时空限制1000ms / 128MB

 提交  题解   

• 提示：收藏到任务计划后，可在首页查看。

最新讨论显示

推荐的相关题目显示

题目描述

石头剪刀布是常见的猜拳游戏:石头胜剪刀,剪刀胜布,布胜石头。如果两个人出拳一 样，则不分胜负。在《生活大爆炸》第二季第8集中出现了一种石头剪刀布的升级版游戏。

升级版游戏在传统的石头剪刀布游戏的基础上,增加了两个新手势:

斯波克:《星际迷航》主角之一。

蜥蜴人:《星际迷航》中的反面角色。

这五种手势的胜负关系如表一所示,表中列出的是甲对乙的游戏结果。

现在,小 A和小 B尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的，但周期长度不一定相等。例如：如果小A以“石头-布-石头-剪刀-蜥蜴人-斯波克”长度为 66 的周期出拳,那么他的出拳序列就是“石头-布-石头-剪刀-蜥蜴人-斯波克-石头-布-石头-剪刀-蜥蜴人-斯波克-......”,而如果小B以“剪刀-石头-布-斯波克-蜥蜴人”长度为 55 的周期出拳,那么他出拳的序列就是“剪刀-石头-布-斯波克-蜥蜴人-剪刀-石头-布-斯波克-蜥蜴人-......”

已知小 A和小 B 一共进行 NN 次猜拳。每一次赢的人得 11 分，输的得 00 分；平局两人都得 00 分。现请你统计 NN次猜拳结束之后两人的得分。

输入输出格式

输入格式：

 

第一行包含三个整数：N,N_A,N_BN,NA​,NB​,分别表示共进行 NN 次猜拳、小 A出拳的周期长度，小 B 出拳的周期长度。数与数之间以一个空格分隔。

第二行包含 N_ANA​ 个整数,表示小 A出拳的规律,第三行包含 N_BNB​ 个整数,表示小 B 出拳的规律。其中，00 表示“剪刀”，11 表示“石头”，22 表示“布”，33 表示“蜥蜴人”，44表示“斯波克”。数与数之间以一个空格分隔。

 

输出格式：

 

输出一行，包含两个整数，以一个空格分隔，分别表示小 A、小 B的得分。

 

输入输出样例

输入样例#1： 复制

10 5 6
0 1 2 3 4
0 3 4 2 1 0

输出样例#1： 复制

6 2

输入样例#2： 复制

9 5 5
0 1 2 3 4
1 0 3 2 4

输出样例#2： 复制

4 4

说明

对于100\%100%的数据，0 < N \leq 200, 0 < N_A \leq 200, 0 < N_B \leq 2000

思路：

开一个的分数组把这25种出拳得分记录一下，之后对于两人的每种出拳得分直接计算就行了，其中注意一下周期（直接取模就好了）

代码：

#pragma GCC optimize ("O3")
#include
using namespace std;
bool play[5][5] = {{0,0,1,1,0},{1,0,0,1,0},{0,1,0,0,1}
                    ,{0,0,1,0,1},{1,1,0,0,0}};
const int maxn = 210;
int a[maxn],b[maxn];
int main()
{
    int n,n1,n2;
    scanf("%d %d %d",&n,&n1,&n2);
    for (int i = 0;i < n1;i ++)
        scanf("%d",&a[i]);
    for (int i = 0;i < n2;i ++)
        scanf("%d",&b[i]);
    int i = 0,s1 = 0,s2 = 0;
    while (n --)
    {
        s1 += play[a[i % n1]][b[i % n2]];
        s2 += play[b[i % n2]][a[i % n1]];
        i ++;
    }
    printf("%d %d\n",s1,s2);
    return 0;
}

P1563 玩具谜题

• • 10K通过
  • 30.8K提交
• 题目提供者CCF_NOI
• 评测方式云端评测
• 标签NOIp提高组2016高性能
• 难度普及-
• 时空限制1000ms / 512MB

 提交  题解   

• 提示：收藏到任务计划后，可在首页查看。

最新讨论显示

推荐的相关题目显示

题目描述

小南有一套可爱的玩具小人, 它们各有不同的职业。

有一天, 这些玩具小人把小南的眼镜藏了起来。 小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:

这时singersinger告诉小南一个谜題: “眼镜藏在我左数第3个玩具小人的右数第11个玩具小人的左数第22个玩具小人那里。 ”

小南发现, 这个谜题中玩具小人的朝向非常关键, 因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人, 它的左边是顺时针方向, 右边是逆时针方向; 而面向圈外的玩具小人, 它的左边是逆时针方向, 右边是顺时针方向。

小南一边艰难地辨认着玩具小人, 一边数着:

singersinger朝内, 左数第33个是archerarcher。

archerarcher朝外,右数第11个是thinkerthinker。

thinkerthinker朝外, 左数第22个是writewriter。

所以眼镜藏在writerwriter这里!

虽然成功找回了眼镜, 但小南并没有放心。 如果下次有更多的玩具小人藏他的眼镜, 或是谜題的长度更长, 他可能就无法找到眼镜了 。 所以小南希望你写程序帮他解决类似的谜題。 这样的谜題具体可以描述为:

有 nn个玩具小人围成一圈, 已知它们的职业和朝向。现在第11个玩具小人告诉小南一个包含mm条指令的谜題, 其中第 zz条指令形如“左数/右数第ss,个玩具小人”。 你需要输出依次数完这些指令后,到达的玩具小人的职业。

输入输出格式

输入格式：

 

输入的第一行包含两个正整数 n,mn,m，表示玩具小人的个数和指令的条数。

接下来 nn 行，每行包含一个整数和一个字符串，以逆时针为顺序给出每个玩具小人的朝向和职业。其中 00 表示朝向圈内，11 表示朝向圈外。 保证不会出现其他的数。字符串长度不超过 1010 且仅由小写字母构成，字符串不为空，并且字符串两两不同。整数和字符串之间用一个空格隔开。

接下来 mm 行，其中第 ii 行包含两个整数 a_i,s_iai​,si​，表示第 ii 条指令。若 a_i=0ai​=0，表示向左数 s_isi​ 个人；若 a_i=1ai​=1，表示向右数 s_isi​ 个人。 保证 a_iai​ 不会出现其他的数，1 \le s_i < n1≤si​

 

输出格式：

 

输出一个字符串，表示从第一个读入的小人开始，依次数完 mm 条指令后到达的小人的职业。

 

输入输出样例

输入样例#1： 复制

7 3
0 singer
0 reader
0 mengbier 
1 thinker
1 archer
0 writer
1 mogician 
0 3
1 1
0 2

输出样例#1： 复制

writer

输入样例#2： 复制

10 10
1 C
0 r
0 P
1 d
1 e
1 m
1 t
1 y
1 u
0 V
1 7
1 1
1 4
0 5
0 3
0 1
1 6
1 2
0 8
0 4

输出样例#2： 复制

y

说明

【样例1说明】

这组数据就是【题目描述】 中提到的例子。

【子任务】

子任务会给出部分测试数据的特点。 如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。

每个测试点的数据规模及特点如下表:

其中一些简写的列意义如下:

• 全朝内: 若为“√”, 表示该测试点保证所有的玩具小人都朝向圈内;

全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的

1≤z≤m, a_i=01≤z≤m,ai​=0;

s= 1s=1:若为“√”,表示该测试点保证所有的指令都只数1个,即对任意的

1≤z≤m,s_i=11≤z≤m,si​=1;

职业长度为11 :若为“√”,表示该测试点保证所有玩具小人的职业一定是一个

长度为11的字符串。

思路：

直接模拟就行了，注意周期的循环是否出圈

代码：

#include
using namespace std;
const int maxn = (int)1e5 + 10;
struct node
{
    bool di;
    string s;
}a[maxn];
int main()
{
    int n,m;
    cin>>n>>m;
    for (int i = 0;i < n;i ++)
        cin>>a[i].di>>a[i].s;
    int p,t,cut = 0;
    while (m --)
    {
        cin>>p>>t;
        if (p == a[cut].di)
            cut -= t;
        else
            cut += t;
        cut %= n;
        if (cut < 0)
            cut += n;
    }
    cout<