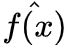关于局部加权回归（Locally Weighted Scatterplot Smoothing，LOWESS）、STL（Seasonal-Trend decomposition procedure based on Loess）算法原理的讨论，以及时序异常检测应用的思考

1. LOWESS（Locally Weighted Scatterplot Smoothing，局部加权回归）

0x1：lowess算法主要解决什么问题

1. 非线性回归拟合问题

LOWESS 通过取一定比例的局部数据，在这部分子集中拟合多项式回归曲线，这样我们便可以观察到数据在局部展现出来的局部规律和局部趋势（局部均值μ回归）。

同时，因为 LOWESS 的统计窗口缩小为局部窗口，因此拟合的回归曲线可以包含周期性，波动性的信息。

和传统的多元线性回归最大的不同是，通常的回归分析往往是根据全体数据建模，这样可以描述整体趋势，但现实生活中规律不总是（或者很少是）一条直线。

LOWESS将局部范围从左往右依次推进，最终一条连续的曲线就被计算出来了。显然，曲线的光滑程度与我们选取数据比例（局部窗口）有关：

• 局部统计窗口比例越少，拟合越不光滑，因为过于看重局部性质。但相对的，拟合的精确度更高
• 局部统计窗口比例越大，拟合越光滑，因为更看重整体性质。但拟合的精确度也相应降低

下面通过一个例子来形象说明"LOWESS"和"Linear regression"在局部信息捕获上的主要区别

数据文件是关于“物种数目与海拔高度”（中科院植物所-赖江山博士），数据集可以在这里下载。

用回归模型拟合的图示如下，本文采用R语言：

# 从counts.txt文件直接将数据读入R
x = read.csv("/Users/zhenghan/Downloads/counts.txt")
print(x)

par(las = 1, mar = c(4, 4, 0.1, 0.1), mgp = c(2.5,
                                              1, 0))
plot(x, pch = 20, col = rgb(0, 0, 0, 0.5))
abline(lm(counts ~ altitude, x), lwd = 2, col = "red")

如果仅仅从回归直线来看，似乎是海拔越高，则物种数目越多。如此推断下去，恐怕月球或火星上该物种最多。这显然是一个不是那么完美的线性回归推断。

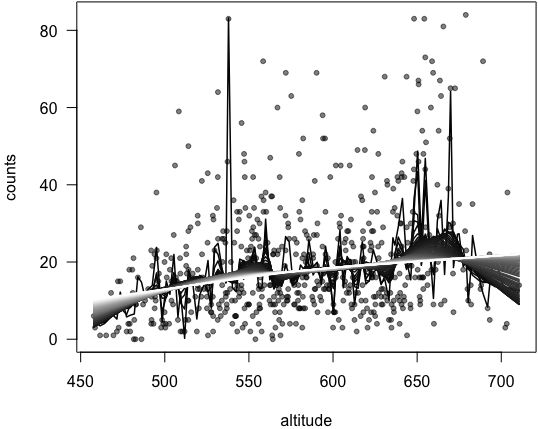
改用lowess进行局部加权回归拟合，图示如下：

# 从counts.txt文件直接将数据读入R
x = read.csv("/Users/zhenghan/Downloads/counts.txt")
print(x)

par(las = 1, mar = c(4, 4, 0.1, 0.1))
plot(x, pch = 20, col = rgb(0, 0, 0, 0.5))
# 取不同的f参数值
for (i in seq(0.01, 1, length = 100)) {
  lines(lowess(x$altitude, x$counts, f = i), col = gray(i),
        lwd = 1.5)
  Sys.sleep(0.15)
}

上图中，曲线颜色越浅表示所取数据比例越大，即数据点越集中。不难看出白色的曲线几乎已呈直线状，而黑色的线则波动较大。

总体看来，图中大致有四处海拔上的物种数目偏离回归直线较严重：450 米、550 米、650 米和 700 米附近。这种偏离回归的现象恰好说明了实际问题的概率分布并不是严格遵循线性回归模型，而是其他的更复杂的非线性模型。

基于LOWESS的拟合结果，若研究者的问题是，多高海拔处的物种数最多？那么答案应该是在 650 米附近。 

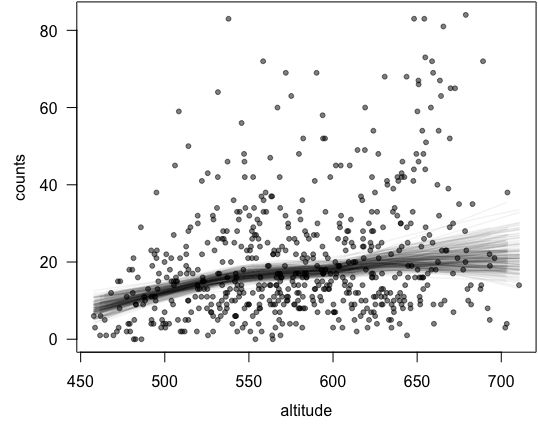
为了确保我们用 LOWESS 方法得到的趋势是稳定的，我们可以进一步用 Bootstrap 的方法验证。因为 Bootstrap 方法是对原样本进行重抽样，根据抽得的不同样本可以得到不同的 LOWESS 曲线，最后我们把所有的曲线添加到图中，看所取样本不同是否会使得 LOWESS 有显著变化。

# 从counts.txt文件直接将数据读入R
x = read.csv("/Users/zhenghan/Downloads/counts.txt")
print(x)

set.seed(711) # 设定随机数种子，保证本图形可以重制
par(las = 1, mar = c(4, 4, 0.1, 0.1), mgp = c(2.5,
                                              1, 0))
plot(x, pch = 20, col = rgb(0, 0, 0, 0.5))
for (i in 1:400) {
  idx = sample(nrow(x), 300, TRUE) # 有放回抽取300个样本序号
  lines(lowess(x$altitude[idx], x$counts[idx]), col = rgb(0,
                                                          0, 0, 0.05), lwd = 1.5) # 用半透明颜色，避免线条重叠使得图形看不清
  Sys.sleep(0.05)
}

可以看出，虽然 700 米海拔附近物种数目减小的趋势并不明显了，这是因为这个海拔附近的观测样本量较少，在重抽样的时候不容易被抽到，因此在图中代表性不足，最后得到的拟合曲线分布稀疏。

但是经过 400 次重抽样并计算 LOWESS 曲线，刚才在第一幅图中观察到的趋势大致都还存在（因为默认取数据比例为 2/3，因此拟合曲线都比较光滑），所以整体回归拟合的结果是可信的。

2. 局部平滑问题

由于样本数据不可避免的随机波动问题（方差存在），我们获得的样本数据总是存在偏离均值的情况，为了更好地体现出数据中的统计规律性，我们需要对数据进行平滑处理。

举一个具体例子来说，在做数据平滑的时候，会有遇到有趋势或者季节性的数据，对于这样的数据，我们不能使用简单的均值正负3倍标准差以外做异常值剔除，需要考虑到趋势性等条件。使用局部加权回归，可以拟合一条趋势线，将该线作为基线，偏离基线距离较远的则是真正的异常值点。 

0x2：从KNN线性回归逐渐演进为LOWESS

上一章节讨论了线性回归在具体工程问题中面临的2个主要挑战，即：

• 周期性、波动性非线性数据回归问题
• 数据系统性噪点（非数据本身包含的方差，而是系统本身固有的方差）的平滑化问题

面对以上问题，学术界的陆续发表了很多研究paper，很好地解决了这些问题，笔者在这里尽量列举和梳理出整个理论体系的发展脉络。

1. 多元非线性回归模型

人们最早提出，用多元线性回归模型来拟合一元线性模型无法拟合的复杂样本数据。但是遇到了几个比较大的问题：

• 多元模型的模型函数需要人工设定，例如根据数据集绘出的图像，半观察半猜测要不要加个自变量的平方项，或者自变量的三角函数等等，作为新的回归算子加入，直到一些评价指标上拟合效果较好为止，这个过程就是非常繁重的特征工程工作
• 多元线性回归很容易陷入overfit或者underfit问题。

2. KNN线性回归

另一个解决问题的思路就是对数据进行局部最近邻处理，也即KNN线性回归。

其中：

• Nk(x)：为距离点x最近k个点xi组成的邻域集合（neighborhood set）
• yi：为KNN均值化后的回归结果
• ：为统计窗口内的回归结果，该统计窗口的所有点都用该点代替

但是，KNN线性回归有几个最大的缺点：

• 没有考虑到不同距离的邻近点应有不同的权重，不管是从统计上还是从领域经验角度来看，偏离均值越远的点重要性理应越低；
• 拟合的曲线不连续（discontinuous），拟合曲线的毛躁点还是很多，例如下图

 

关于KNN线性回归的问题的其他讨论，可以参阅这篇文章。

3. 引入kernel加权平滑的KNN线性回归

解决传统KNN线性回归问题的一个思考方向是：避免直接求均值这种“hard regression”的方式，改为寻找一种“soft regression”的方式。

我们在原始的KNN公式之上引入加权平滑：

权重因子函数K可以由很多种形式，一个大的原则就是：偏离均值越远的点，其贡献度相对越低。

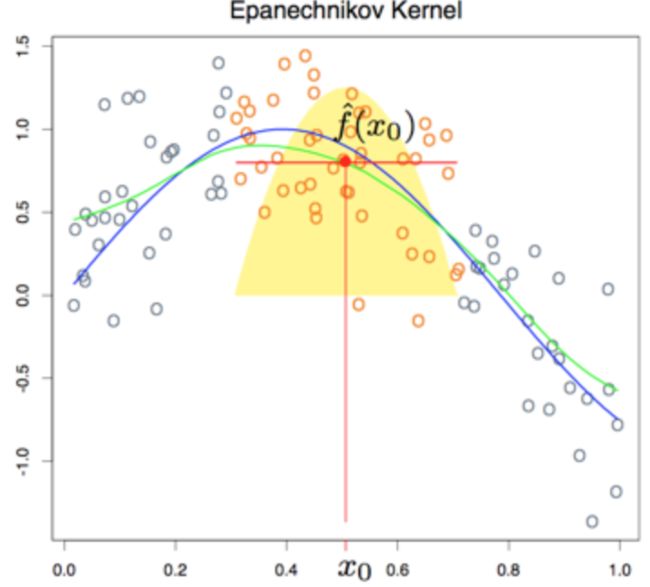
比如，Epanechnikov二次kernel：

，

其中，λ为kernel的参数，称之为window width。对于KNN，只考虑最近的k个点影响；基于此，

，其中，x[k]为距离x0第k近的点，即窗口边界点。

经kernel加权平滑后，原始的KNN回归拟合的曲线为连续的了，如下图：

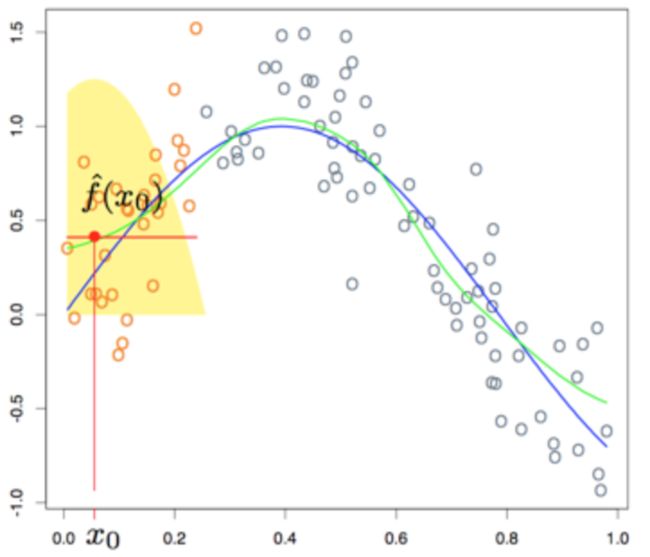
但是，这种kernel回归同样存在着边界（boundary）问题，如下图：

4. 基于最大似然估计的kernel加权平滑KNN回归

上一小节我们看到，传统kernel加权平滑的KNN回归，对于x序列的开始与结束区段的点，其左右邻域是不对称的，导致了平滑后的值偏大或偏小。

因此，需要对权值做再修正，修正的方法就是再次基于窗口内的数据点极大似然估计，使回归值x0进一步向均值线μ靠拢。

假定对统计窗口的回归量x0的估计值为：

定义目标函数：

令：

，

那么，目标函数可改写为：

求偏导，可得到：

利用矩阵运算，可直接得极大似然估计值为：

其中，

上述回归方法称之为LOWESS (Local Weighted regression)。

5. Robust LOWESS

我们沿着LOWESS的思路脉络继续讨论，截止目前为止，LOWESS似乎圆满地完成了所有任务，但是还有一个问题，就是样本数据中的异常点（outlier）问题。

我们知道，样本数据中的方差波动来自两个方面：

• 系统性误差：由于采样和测量手段引起的误差，不可避免
• 样本自身误差：由于样本数据自身存在的固有方差波动，导致的离群点

样本数据集的总体分布由以上两种方差波动共同作用产生，LOWESS通过kernel加权和极大似然回归的方式已经起到了较好的均值回归的作用，但是在极端的离群点（outlier）情况下，LOWESS的回归点x0依然可能偏离真值均值点μ过远。因此，人们又提出了Robust LOWESS方法。

Robust LOWESS是Cleveland在LOWESS基础上提出来的robust回归方法，能避免outlier对回归的影响。

在计算完估计值后，继续计算残差：

根据残差计算robustnest weight：

其中，s为残差绝对值序列的中位值（median），B函数为bisquare函数：

然后，用robustness weight乘以kernel weight作为的新weight。如此，便剔除了残差较大的异常点对于回归的影响，这本质上是数理统计中随机变量标准化的一种思想应用。

0x3：LOWESS对sin正弦周期数据的拟合效果测试

为了验证LOWESS的实际性能，我们来构造一组数据集验证其效果，该数据集的特性满足：

• 周期性：数据集不是单纯的线性回归关系，而是包含了周期波动性，我们基于sin函数生成y值
• 随机性：数据在不同的局部窗口中的密度分布是不同的，因此在不同局部窗口之间，均值并不是稳定连续变化的

lowess.py库函数

"""
lowess: Locally linear regression
==================================

Implementation of the LOWESS algorithm in n dimensions.

References
=========
[HTF] Hastie, Tibshirani and Friedman (2008). The Elements of Statistical
Learning; Chapter 6

[Cleveland79] Cleveland (1979). Robust Locally Weighted Regression and Smoothing
Scatterplots. J American Statistical Association, 74: 829-836.

"""
import numpy as np
import numpy.linalg as la


# Kernel functions:
def epanechnikov(xx, **kwargs):
    """
    The Epanechnikov kernel estimated for xx values at indices idx (zero
    elsewhere)

    Parameters
    ----------
    xx: float array
        Values of the function on which the kernel is computed. Typically,
        these are Euclidean distances from some point x0 (see do_kernel)

    Notes
    -----
    This is equation 6.4 in HTF chapter 6

    """
    l = kwargs.get('l', 1.0)
    ans = np.zeros(xx.shape)
    xx_norm = xx / l
    idx = np.where(xx_norm <= 1)
    ans[idx] = 0.75 * (1 - xx_norm[idx] ** 2)
    return ans


def tri_cube(xx, **kwargs):
    """
    The tri-cube kernel estimated for xx values at indices idx (zero
    elsewhere)

    Parameters
    ----------
    xx: float array
        Values of the function on which the kernel is computed. Typically,
        these are Euclidean distances from some point x0 (see do_kernel)

    idx: tuple
        An indexing tuple pointing to the coordinates in xx for which the
        kernel value is estimated. Default: None (all points are used!)

    Notes
    -----
    This is equation 6.6 in HTF chapter 6
    """
    ans = np.zeros(xx.shape)
    idx = np.where(xx <= 1)
    ans[idx] = (1 - np.abs(xx[idx]) ** 3) ** 3
    return ans


def bi_square(xx, **kwargs):
    """
    The bi-square weight function calculated over values of xx

    Parameters
    ----------
    xx: float array

    Notes
    -----
    This is the first equation on page 831 of [Cleveland79].
    """
    ans = np.zeros(xx.shape)
    idx = np.where(xx < 1)
    ans[idx] = (1 - xx[idx] ** 2) ** 2
    return ans


def do_kernel(x0, x, l=1.0, kernel=epanechnikov):
    """
    Calculate a kernel function on x in the neighborhood of x0

    Parameters
    ----------
    x: float array
       All values of x
    x0: float
       The value of x around which we evaluate the kernel
    l: float or float array (with shape = x.shape)
       Width parameter (metric window size)
    kernel: callable
        A kernel function. Any function with signature: `func(xx)`
    """
    # xx is the norm of x-x0. Note that we broadcast on the second axis for the
    # nd case and then sum on the first to get the norm in each value of x:
    xx = np.sum(np.sqrt(np.power(x - x0[:, np.newaxis], 2)), 0)
    return kernel(xx, l=l)


def lowess(x, y, x0, deg=1, kernel=epanechnikov, l=1, robust=False, ):
    """
    Locally smoothed regression with the LOWESS algorithm.

    Parameters
    ----------
    x: float n-d array
       Values of x for which f(x) is known (e.g. measured). The shape of this
       is (n, j), where n is the number the dimensions and j is the
       number of distinct coordinates sampled.

    y: float array
       The known values of f(x) at these points. This has shape (j,)

    x0: float or float array.
        Values of x for which we estimate the value of f(x). This is either a
        single scalar value (only possible for the 1d case, in which case f(x0)
        is estimated for just that one value of x), or an array of shape (n, k).

    deg: int
        The degree of smoothing functions. 0 is locally constant, 1 is locally
        linear, etc. Default: 1.

    kernel: callable
        A kernel function. {'epanechnikov', 'tri_cube', 'bi_square'}

    l: float or float array with shape = x.shape
       The metric window size for the kernel

    robust: bool
        Whether to apply the robustification procedure from [Cleveland79], page
        831


    Returns
    -------
    The function estimated at x0.

    Notes
    -----
    The solution to this problem is given by equation 6.8 in Hastie
    Tibshirani and Friedman (2008). The Elements of Statistical Learning
    (Chapter 6).

    Example
    -------
    >>> import lowess as lo
    >>> import numpy as np

    # For the 1D case:
    >>> x = np.random.randn(100)
    >>> f = np.cos(x) + 0.2 * np.random.randn(100)
    >>> x0 = np.linspace(-1, 1, 10)
    >>> f_hat = lo.lowess(x, f, x0)
    >>> import matplotlib.pyplot as plt
    >>> fig, ax = plt.subplots(1)
    >>> ax.scatter(x, f)
    >>> ax.plot(x0, f_hat, 'ro')
    >>> plt.show()

    # 2D case (and more...)
    >>> x = np.random.randn(2, 100)
    >>> f = -1 * np.sin(x[0]) + 0.5 * np.cos(x[1]) + 0.2*np.random.randn(100)
    >>> x0 = np.mgrid[-1:1:.1, -1:1:.1]
    >>> x0 = np.vstack([x0[0].ravel(), x0[1].ravel()])
    >>> f_hat = lo.lowess(x, f, x0, kernel=lo.tri_cube)
    >>> from mpl_toolkits.mplot3d import Axes3D
    >>> fig = plt.figure()
    >>> ax = fig.add_subplot(111, projection='3d')
    >>> ax.scatter(x[0], x[1], f)
    >>> ax.scatter(x0[0], x0[1], f_hat, color='r')
    >>> plt.show()
    """
    if robust:
        # We use the procedure described in Cleveland1979
        # Start by calling this function with robust set to false and the x0
        # input being equal to the x input:
        y_est = lowess(x, y, x, kernel=epanechnikov, l=l, robust=False)
        resid = y_est - y
        median_resid = np.nanmedian(np.abs(resid))
        # Calculate the bi-cube function on the residuals for robustness
        # weights:
        robustness_weights = bi_square(resid / (6 * median_resid))

    # For the case where x0 is provided as a scalar:
    if not np.iterable(x0):
        x0 = np.asarray([x0])

    #print "x0: ", x0
    ans = np.zeros(x0.shape[-1])
    # We only need one design matrix for fitting:
    B = [np.ones(x.shape[-1])]
    for d in range(1, deg + 1):
        B.append(x ** deg)

    #print "B: ", B

    B = np.vstack(B).T
    for idx, this_x0 in enumerate(x0.T):
        # This is necessary in the 1d case (?):
        if not np.iterable(this_x0):
            this_x0 = np.asarray([this_x0])
        # Different weighting kernel for each x0:
        W = np.diag(do_kernel(this_x0, x, l=l, kernel=kernel))
        # XXX It should be possible to calculate W outside the loop, if x0 and
        # x are both sampled in some regular fashion (that is, if W is the same
        # matrix in each iteration). That should save time.

        print "W: ", W
        if robust:
            # We apply the robustness weights to the weighted least-squares
            # procedure:
            robustness_weights[np.isnan(robustness_weights)] = 0
            W = np.dot(W, np.diag(robustness_weights))
        # try:
        # Equation 6.8 in HTF:
        BtWB = np.dot(np.dot(B.T, W), B)
        BtW = np.dot(B.T, W)
        # Get the params:
        beta = np.dot(np.dot(la.pinv(BtWB), BtW), y.T)
        # We create a design matrix for this coordinat for back-predicting:
        B0 = [1]
        for d in range(1, deg + 1):
            B0 = np.hstack([B0, this_x0 ** deg])
        B0 = np.vstack(B0).T
        # Estimate the answer based on the parameters:
        ans[idx] += np.dot(B0, beta)
    # If we are trying to sample far away from where the function is
    # defined, we will be trying to invert a singular matrix. In that case,
    # the regression should not work for you and you should get a nan:
    # except la.LinAlgError :
    #    ans[idx] += np.nan
    return ans.T

test_lowess.py

# -*- coding: utf-8 -*-

import numpy as np
import numpy.testing as npt
import lowess as lo
import matplotlib.pyplot as plt

def test_lowess():
    """
    Test 1-d local linear regression with lowess
    """
    np.random.seed(1984)
    for kernel in [lo.epanechnikov, lo.tri_cube]:
        for robust in [True, False]:
            # constructing a batch of periodic and volatile data
            x = np.random.randn(100)
            f = np.sin(x)
            x0 = np.linspace(-1, 1, 10)     # x0 means fixed length window width
            f_hat = lo.lowess(x, f, x0, kernel=kernel, l=1.0, robust=robust)
            #print f_hat
            f_real = np.sin(x0)

            plt.figure()
            plt.plot(x0, f_hat, label="lowess fitting curve", color='coral')
            plt.plot(x0, f_real, label="real sin curve", color='blue')

            plt.show()


if __name__ == '__main__':
    np.random.seed(1984)
    kernel = lo.epanechnikov
    robust = True

    # constructing a batch of periodic and volatile data
    x = np.random.randn(100)
    f = np.sin(x)
    x0 = np.linspace(-1, 1, 10)  # x0 means fixed length window width
    f_hat = lo.lowess(x, f, x0, kernel=kernel, l=1.0, robust=robust)
    # print f_hat
    f_real = np.sin(x0)

    plt.figure()
    plt.plot(x0, f_hat, label="lowess fitting curve", color='coral')
    plt.plot(x0, f_real, label="real sin curve", color='blue')

    plt.show()

可以看到，lowess的拟合回归线（橙红色）相对比较好地拟合了原始数据集的。 

0x4：LOWESS和深度神经网络在思想上的同源与联系

这个章节，笔者将尝试把LOWESS和深度神经网络进行类比，通过类比，我们可以更加深入理解LOWESS的思想本质。

1. 如何解决非线性问题

在这点上，深度神经网络用多元神经元叠加的方式，并通过分配不同的权重比来得到一个复杂非线性拟合；而LOWESS的解决思路是缩小统计窗口，在小范围内的窗口内进行回归分析，这也是微积分思想的一种体现。

从模型能力上来说，深度神经网络更适合拟合复杂非线性大网络，而LOWESS更适合拟合周期性波动数据。

2. 如何解决离群异常点问题

在解决这个问题上，LOWESS和深度神经网络殊途同归，都采用了非线性函数进行权重重分配与调整。在深度神经网络中，这被称之为激活函数，在LOWESS中则被称之为kernel加权函数。

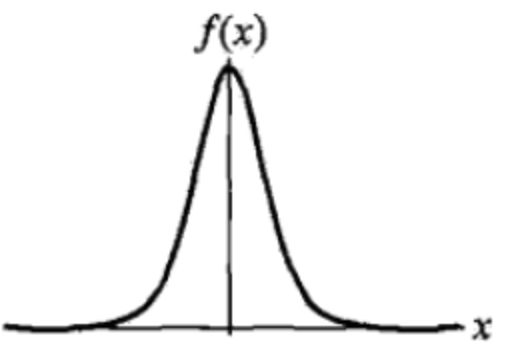
实际上，如果我们将“Epanechnikov二次kernel”和“sigmoid函数的导数”图像分别打印出来，会发现其函数形态都类似于下图：

所以它们发挥的作用也是类似的，即：对远离均值μ回归线的离群点，赋值更小的权重；对靠近均值μ的数据点，赋值更大的权重。

从概率论的角度来说，这种非线性函数的加入本质上也是一种先验假设，先验假设的加入，使得数据驱动的后验估计更加准确，这也是贝叶斯估计思想的核心。

另一方面来说，深度神经网络和深度学习的发展，使得人们可以用深度神经网络构建出一个超复杂的多元非线性网络，对目标数据进行拟合，并通过剪枝/dropout等方式缓解过拟合的发生。

Relevant Link: 

https://cosx.org/2008/11/lowess-to-explore-bivariate-correlation-by-yihui/
https://cosx.org/tags/lowess
https://github.com/arokem/lowess
https://blog.csdn.net/longgb123/article/details/79520982
https://www.jianshu.com/p/0002f27e80f9?utm_campaign=maleskine&utm_content=note&utm_medium=seo_notes&utm_source=recommendation
https://cloud.tencent.com/developer/article/1111722 
https://www.cnblogs.com/en-heng/p/7382979.html

0x5：LOWESS用于预测模型

首先要注意的是，和KNN一样，LOWESS是一种非参数（nonparametric）回归模型。模型训练结束后并不能得到一组确定的模型参数（coefficient）。

究其本质原因是因为KNN/LOWESS在训练并没有预先假定一种固定的模型函数公式，相反，KNN/LOWESS直接基于原始数据得到一条多项式拟合曲线，所以很多时候，我们也可以称其为平滑算法。

非参数回归具备很多良好的特性，例如：

• 关于两个变量（X，Y）的关系探索是开放式的，不套用任何现成的数学函数，即不做任何先验假设
• 所拟合的曲线可以很好地描述变量之间的细微变化、局部变化、周期性特征等信息
• 非参数回归提供的是万能的拟合曲线，不管多么复杂的曲线关系都能进行成功的拟合。

基于这个理论前提，非参数模型是无法对未知输入进行预测的，但是可以对训练集范围内的x值进行预测。

我们通过分析KNN的预测能力来解释这句话，KNN模型本质上是一个非参数模型，但其又可以进行预测，这并不矛盾，KNN model存储的本质上是一个非常庞大的参数，也可以说是将整个训练集作为参数存储起来了。在预测时，KNN.predict要求输入值x必须在训练集范围之内，而KNN所谓的最近邻搜索其本质上和插值法在思想上是一致的。

回到LOWESS的预测任务上，LOWESS.predict要求输入的x值必须在训练数据范围内。

Relevant Link: 

http://webcache.googleusercontent.com/search?q=cache:EgbwJKBCol8J:landcareweb.com/questions/44622/shi-yong-ju-bu-jia-quan-hui-gui-loess-lowess-yu-ce-xin-shu-ju+&cd=2&hl=zh-CN&ct=clnk

 

2. 时间序列分解算法（STL，Seasonal-Trend decomposition procedure based on Loess）

0x1：时域数据中周期性信号的分解本质是信号从时域到频域的转换

傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

如下图所示，即为时域信号与不同频率的正弦波信号的关系：

上图中最右侧展示的是时域中的一个信号，这是一个近似于矩形的波。而图的正中间则是组成该信号的各个频率的正弦波。

从图中我们可以看出，即使角度几乎为直角的正弦波，其实也是由众多的弧度圆滑的正弦波来组成的。

在时域图像中，我们看到的只有一个矩形波，但当我们通过傅里叶变换将该矩形波转换到频域之后，我们能够很清楚的看到许多脉冲，其中频域图中的横轴为频率，纵轴为振幅。因此可以通过这个频域图像得知，时域中的矩形波是由这么多频率的正弦波叠加而成的。

时序信号本质上也是由很多冲击信号叠加而成的，从时域上，我们看到的是一条不规整的，上下起伏的曲线，但是通过STL分解，我们可以将其分解为不同的信号组成部分。STL的本质就是信号的成分分解，这是STL的核心。

0x2：STL主要解决什么问题

STL（Seasonal and Trend decomposition using Loess）是一种分解时间序列信号的方法，由 Cleveland et al. (1990) 提出。

我们下面解释STL算法主要解决的两个问题，也是STL的主要应用场景。

1. 信号分解与提取

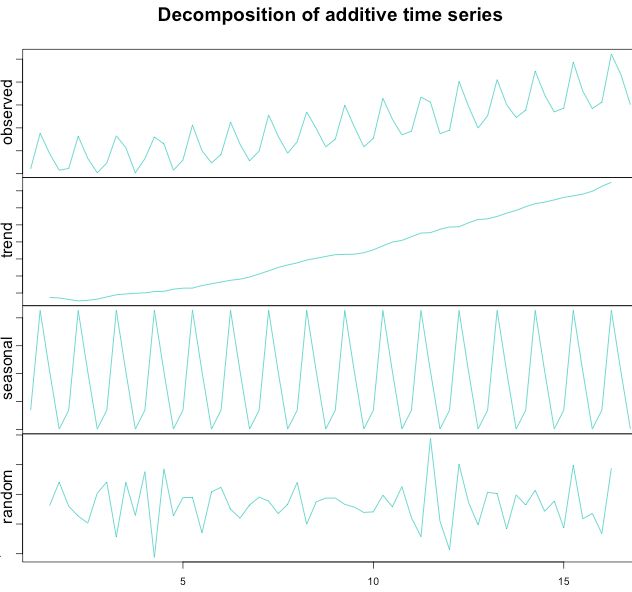
时间序列分解算法主要被用来测定及提取时间序列信号中的趋势性和季节性信号，其分解式为：

，其中

• Tt：表示趋势分量（trend component）
• St：表示周期分量（seasonal component）
• Rt：表示余项（remainder component）

所以本质上，STL是一个信号分解算法。

2. 时序信号趋势性和季节性统计量的定义

基于STL信号分解公式，我们可以使用概率论与数理统计里的方法论对时序信号建立统计量，分别是趋势性强度和季节性强度，它们都以随机变量概率的形式定义。

这两个度量方法非常实用，当我们需要在很多时间序列中找到趋势性或季节性最强的序列，就可以基于这两个统计量进行筛选。 

1）趋势性强度

对于趋势性很强的数据，经季节调整后的数据应比残差项的变动幅度更大，因此会相对较小。但是，对于没有趋势或是趋势很弱的时间序列，两个方差应大致相同。因此，我们将趋势强度定义为：

这可以给趋势强度的衡量标准，其值在0-1之间。因为有些情况下残差项的方差甚至比季节变换后的序列还大，我们令${\mathrm{FT可取的最小值为0。}}^{}$

${\mathrm{2）季节性强度}}^{}$

季节性的强度定义如下

当季节强度${\mathrm{FS接近0时表示该序列几乎没有季节性，当季节强度FS接近1时表示该序列的Var(Rt)远小于var(St+Rt)。}}^{}$

0x3：STL算法整体框架性架构

STL的整体框架性结构如下

笔者会在这个章节先进行框架性和原理性的讨论，不涉及具体的算法细节，某个部分也会进行简化处理，目的是总整体上对STL建立一个感性的认识。

1. 数据拆分规则

数据拆分规则是说我们采用什么模型来表征时序数据的叠加方式。

1）加法方式

原始数据 = 平均季节数据 + 趋势数据 + 残差

这种方式，随着时间的推移季节数据不会有太大的变化，在周期的业务数据更适合这样的拆分方式，我们在工业场景中用的最多的也是这种分解方式。

加法方式也是傅里叶变换时域信号分解的信号叠加方式。

2）乘法方式

原始数据 = 季节数据 * 趋势数据 * 残差

这种分解方式，随着时间的推移季节数据波动会非常明显。 

2. 确定数据周期

要从时序信号中提取出周期性信号，首要的事情是需要确定时序周期，即多久循环一次的时间窗口长度。时序周期的确定大概有两个方法：

• 根据业务经验人工设定：例如像博客园访客趋势这种业务场景，时序周期显然应该设定为7天。大部分项目中，我们都是采用人工设定的方式
• 基于傅里叶变换技术从样本数据中自动提取

3. 提取趋势数据

从时序数据中抽取趋势信息，最合理的方法就是寻找均值回归线，均值回归线反映了时序数据整体的趋势走向。

上图是分解后形成了：趋势数据 + 其他数据。
下图是去到其他数据最终的趋势数据。

在STL中，趋势信息的提取是通过LOWESS算法实现的。

4. 提取季节周期性数据

得到了趋势数据之后，接下来才可以计算季节周期性数据。计算公式如下：

原始数据 - 趋势数据 = 季节数据 + 残差数据 = S

接下来通过周期均值化从S中提取季节周期性数据。

数据集S中对不同周期中，相同时间点数据的进行相加得到数据集SP，然后除以原始数据的周期数c，得到一个平均季节数据集H，然后复制c次数据集H，将得到平均季节数据，如下图：

5. 提取残差数据

残差数据的获取公式如下：

原始数据 - 趋势数据 - 平均季节数据 = 残差数据 

最终分解为不同的信号部分的结果如下：

 

0x4：STL分解算法流程细节

首先，STL是一个迭代循环，总体思想有点类似EM算法的分布优化过程，通过多轮迭代，逐步逼近“趋势信号”和“周期信号”的概率分布真值。

STL分为内循环（inner loop）与外循环（outer loop），其中内循环主要做了趋势拟合与周期分量的计算。外层循环主要用于调节robustness weight，即去除outlier离群点。

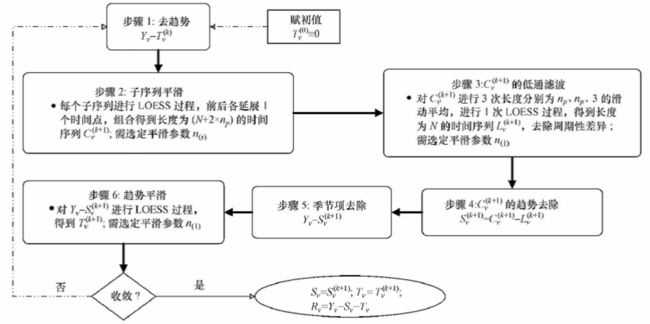
1. STL内循环

下图为STL内循环的流程图：

1）初始化

内循环从趋势分量开始，初始化。

初始化完成后内循环。

2）Step-1：去趋势分量

将本轮的总信号量，减去上一轮结果的趋势分量，

3）Step-2：去除季节周期性信号

去除完趋势分量之后，余下的信号主要由两部分组成，即”残差信号+季节周期性信号“，接下来要做的事是提取出季节周期性信号。我们分几小步讨论。

3.1）周期子序列平滑（Cycle-subseries smoothing）

将每个周期间相同位置的样本点（周期平移后相同位置）组成一个子序列集合（subseries），容易知道这样的子序列个数等于Np个（一个周期内的样本数为Np），我们称其为cycle-subseries，记为。

用对每个子序列做局部加权回归，并向前向后各延展一个周期，其中n(s)为LOESS平滑参数。

所有LOESS平滑结果组成一个”Temporary seasonal series（临时周期季节性子序列集合）“，集合长度为：N+2*Np，其中N为时序信号总长度。

3.2）周期子序列的低通量过滤（Low-Pass Filtering）- 提取周期子序列中的非周期性信号 

对上一个步骤的”temporary seasonal series”依次做长度为n(p)、n(p)、3的滑动平均（moving average），其中n(p)为一个周期的样本数。

然后做回归，得到结果序列，相当于提取周期子序列的低通量，即周期子序列信号中的低通噪音信号，也可以理解为周期子序列中的趋势信号。

3.3）去除平滑周期子序列趋势（Detrending of Smoothed Cycle-subseries）- 周期子序列周期信号提纯

提纯后得到季节周期性信号。

3.4）去除周期性信号

4）Step-3：趋势平滑（Trend Smoothing）- 提取下一轮迭代中需要用到的趋势信号

对于去除周期之后的序列做回归，其中n(t)是LOESS平滑参数，得到下一轮的趋势分量。

之后需要判断是否收敛，如果未收敛则继续下一轮迭代，如果收敛则输出本轮迭代的最终“趋势分量结果”与“周期分量结果”。

2. STL外循环 

外层循环主要用于调节LOESS算法的robustness weight。如果数据序列中有outlier，则余项会较大。

具体细节可以参阅文章前面对LOWESS的robustness weight的相关讨论。

为了使得算法具有足够的robustness，所以设计了内循环与外循环。特别地，当内存循环数足够大时，内循环结束时趋势分量与周期分量已收敛；

同时，若时序数据中没有明显的outlier，可以将外层循环数设为0。

0x5：STL信号分解代码示例 

# -*- coding: utf-8 -*-

import statsmodels.api as sm
import matplotlib.pyplot as plt
import pandas as pd

from datetime import datetime
from heapq import nlargest
from re import match
import pytz
import numpy as np

def datetimes_from_ts(column):
    return column.map(
        lambda datestring: datetime.fromtimestamp(int(datestring), tz=pytz.utc))

def date_format(column, format):
    return column.map(lambda datestring: datetime.strptime(datestring, format))

def format_timestamp(indf, index=0):
    if indf.dtypes[0].type is np.datetime64:
        return indf

    column = indf.iloc[:,index]

    if match("^\\d{4}-\\d{2}-\\d{2} \\d{2}:\\d{2}:\\d{2} \\+\\d{4}$",
             column[0]):
        column = date_format(column, "%Y-%m-%d %H:%M:%S")
    elif match("^\\d{4}-\\d{2}-\\d{2} \\d{2}:\\d{2}:\\d{2}$", column[0]):
        column = date_format(column, "%Y-%m-%d %H:%M:%S")
    elif match("^\\d{4}-\\d{2}-\\d{2} \\d{2}:\\d{2}$", column[0]):
        column = date_format(column, "%Y-%m-%d %H:%M")
    elif match("^\\d{2}/\\d{2}/\\d{2}$", column[0]):
        column = date_format(column, "%m/%d/%y")
    elif match("^\\d{2}/\\d{2}/\\d{4}$", column[0]):
        column = date_format(column, "%Y%m%d")
    elif match("^\\d{4}\\d{2}\\d{2}$", column[0]):
        column = date_format(column, "%Y/%m/%d/%H")
    elif match("^\\d{10}$", column[0]):
        column = datetimes_from_ts(column)

    indf.iloc[:,index] = column

    return indf

def get_gran(tsdf, index=0):
    col = tsdf.iloc[:,index]
    n = len(col)

    largest, second_largest = nlargest(2, col)
    gran = int(round(np.timedelta64(largest - second_largest) / np.timedelta64(1, 's')))

    if gran >= 86400:
        return "day"
    elif gran >= 3600:
        return "hr"
    elif gran >= 60:
        return "min"
    elif gran >= 1:
        return "sec"
    else:
        return "ms"



if __name__ == '__main__':
    # https://github.com/numenta/NAB/blob/master/data/artificialWithAnomaly/art_daily_flatmiddle.csv
    dta = pd.read_csv('./art_daily_flatmiddle.csv', usecols=['timestamp', 'value'])
    dta = format_timestamp(dta)
    dta = dta.set_index('timestamp')
    dta['value'] = dta['value'].apply(pd.to_numeric, errors='ignore')
    dta.value.interpolate(inplace=True)

    print "dta.value: ", dta.value
    res = sm.tsa.seasonal_decompose(dta.value, freq=288)
    res.plot()
    plt.show()

0x6：基于STL信号分解算法的应用

1. STL时序预测

STL时间序列分解算法不仅本质上在学习时间序列中和在探索历史随之间变化中十分有用，它也可以应用在预测中。

假设一个加法分解，分解后的时间序列可以写为：

其中，St代表季节周期性信号，At代表趋势性和残差信号的混合。

对于时间序列的预测，我们需要分别预测季节项${\stackrel{}{}}^{}$

${\stackrel{}{}}^{}$

另一方面，可以使用任意非季节性预测方法来预测分量At。例如，可以使用带漂移项的随机游走法，也可以使用三次指数平滑法（Holt-Winters法），或者还可以用非季节性的ARIMA模型。

我们这里以双色球为例，基于历史双色球开奖的记录作为时序数据，预测未来可能的双色球开奖结果。

# -*- coding: utf-8 -*-

import statsmodels.api as sm
import matplotlib.pyplot as plt
import pandas as pd
import os
import numpy as np
import pickle
import pandas
from statsmodels.tsa.api import Holt


def load_historydata():
    # http://www.17500.cn/getData/ssq.TXT
    if not os.path.isfile("./ssq.pkl"):
        ori_data = np.loadtxt('./ssq.TXT', delimiter=' ', usecols=(0, 2, 3, 4, 5, 6, 7, 8), unpack=False)
        pickle.dump(ori_data, open("./ssq.pkl", "w"))
        df = pandas.DataFrame(data=ori_data)
        return df
    else:
        ori_data = pickle.load(open("./ssq.pkl", "r"))
        df = pandas.DataFrame(data=ori_data)
        return df


if __name__ == '__main__':
    dta = load_historydata()
    #print dta

    dta = dta.set_index(0)
    # Interpolate values
    for i in [1, 2, 3, 4, 5, 6, 7]:
        dta[i].interpolate(inplace=True)

    print dta

    # show the stl decomposition result
    for i in [1, 2, 3, 4, 5, 6, 7]:
        res = sm.tsa.seasonal_decompose(dta[i], freq=7)
        res.plot()
    plt.show()


    # predict the future time series data
    y_pred = []
    for j in range(1, 8):
        y_hat = []
        for i in [1, 2, 3, 4, 5, 6, 7]:
            fit = Holt(np.asarray(dta[i])).fit(smoothing_level=0.3, smoothing_slope=0.1)
            y_hat.append(int(fit.forecast(j)[-1]))
        y_pred.append(y_hat)

    print "y_pred: ", y_pred

从STL分解结果残差信号可以看出，双色球的开奖结果的具备很大的随机性，并没有呈现出明显的季节周期性和趋势性。

这里预测了8天的未来开奖结果如下：

[
    [5, 14, 18, 22, 26, 30, 8], 
    [5, 14, 18, 22, 26, 30, 8], 
    [5, 15, 18, 22, 26, 30, 8], 
    [5, 15, 18, 23, 26, 30, 8], 
    [5, 15, 18, 23, 26, 30, 7], 
    [5, 16, 19, 23, 26, 30, 7], 
    [5, 16, 19, 23, 26, 30, 7]
]

Relevant Link:  

https://otexts.com/fppcn/forecasting-decomposition.html
http://www.sunsoda.fun/TS%E6%97%B6%E9%97%B4%E5%88%86%E6%9E%90(3).html

2. 时序信号异常检测

从时序信号中提取出残差数据后，我们可以基于此做时序异常检测，时序数据如果有异常，都会体现在残差数据集中。下面列举几种对残差信号进行异常检测的方法：

1）残差信号假设检验

假设残差数据满足正太分布，或者近似正太分布，可以计算出残差数据集的标准差。

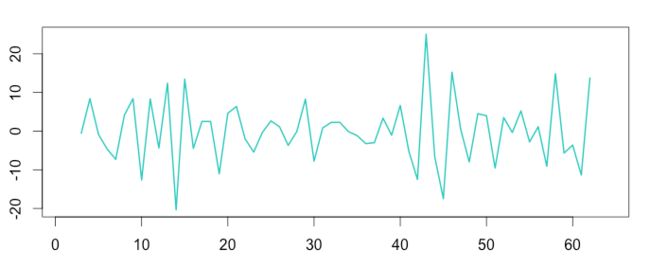
如果数据点与均值的差值绝对值在3倍标准差外，则认为是异常点，也就是3sigma异常检验，例如下面的残差信号图：

2）Generalized Extreme Studentized Deviate (GESD)

GESD，又名Grubb's Test检验，是一种多轮迭代发现多个异常点的异常发现算法。关于grubb's test的讨论，可以参阅另一篇文章。

Relevant Link: 

https://github.com/numenta/NAB
https://github.com/andreas-h/pyloess 
http://siye1982.github.io/2018/03/02/anomaly-detection1/
https://www.cnblogs.com/runner-ljt/p/5245080.html 
https://www.cnblogs.com/en-heng/p/7390310.html 
https://zhuanlan.zhihu.com/p/34342025

 

3. 时序异常检测的应用思考

0x1：什么问题场景下适合用时序异常检测

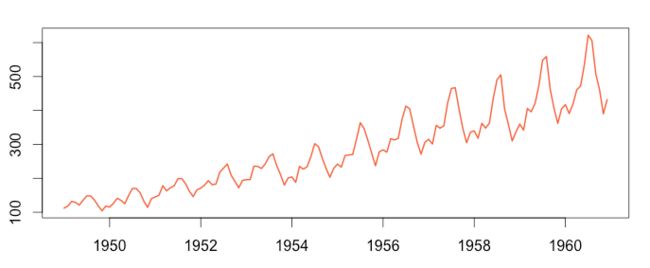
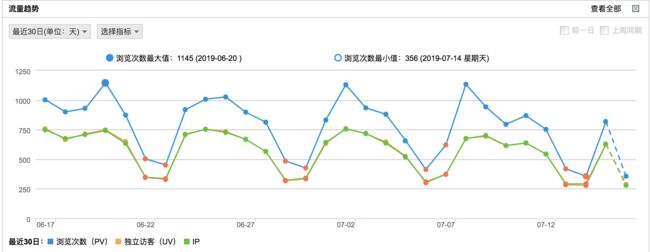
这里拉取了笔者在博客园放置的cnzz来访者统计js插件的流量趋势统计结果

可以看到，我的博客园站点访问呈现明显的周期波动性，但是仔细观察也会发现，在这个周期性之上，趋势线中依然存在几个“看起来不是那么正常”的“离群点”，这些离群点就是因为笔者发表了一些新文章或者什么其他的原因导致访问流量发生非周期性的趋势波动。

抛开具体的实际场景案例，抽象地来说，时间序列的异常检测问题通常表示为：在时变信息系统下，相对于某些标准信号或周期规律性信号的离群点，

时序信号中有很多的异常类型，但是我们只关注业务角度中最重要的类型，比如意外的峰值、下降、趋势变化以及等级转换。

我们下面通过博客园的访问趋势来举例说明典型的时序异常。

1. 附加异常

举个例子来说，笔者发现每逢周末博客园访问量都会下降，而到周一又会回到峰值，但是如果我们发现某个周末访问量突然出现一个异常增加，看起来就像一个峰值。这些类型的异常通常称为附加异常。这种情况很可能是因为笔者在周末发表了一篇新博客。

2. 时间变化异常

关于博客园的另一个例子是，当某天博客园服务器宕机，我们会发现在某个时间段内有零个或者非常少的用户访问，明显和平时的趋势不同，这些类型的异常通常被分类为时间变化异常。

3. 水平位移或季节性水平位移异常

还是以博客园为例，我们假设国家修改了法定假日的时间，从周六/日改到周一/二，那么可以想象，整体的访问趋势会平移2天，每周的低谷平移到周一/二。

这些类型的变化通常被称为水平位移或季节性水平位移异常。

总体来说，异常检测算法应该将每个时间点标记为异常/非异常，或者预测某个点的信号，并衡量这个点的真实值与预测值的差值是否足够大，从而将其视为异常。

0x2：基于STL时序分解算法做时序异常检测的整体思路

这个章节笔者尝试从具体应用场景的角度出发，讨论下怎么基于STL分解算法做时序异常检测。

1. 分析数据源是否具备时序周期性

包括STL在内，很多时序算法都有一个默认的假设前提，即：数据源本身是由周期性的冲击信号源产生的，即数据本身具备季节周期性。

典型的正例子包括网站访问pv量，一般来说是存在【天单位周期性】，因为一般来说，网站的pv访问量每天是呈现相对固定的起伏波动的。

典型的反例包括每期的双色球开奖结果，其数据本身并不存在明显的周期性，所以STL无法从其中提取出任何有概率显著意义的周期性信号，自然也无法基于残差信号做异常检测了。

从笔者自己的经验来看，这个假设前提就极大限制了时序算法在安全领域里的应用，从这个角度来分析，时序异常算法可能只适合在网站cc，服务器ddos，异常运维操作，kpi异常检测等场景应用。

2. 确定时序周期

确认了问题场景的数据适合于时序算法的假设前提后，接下来的问题就是：数据的周期性窗口多大。

例如网站pv访问量的周期可以设置为1天，外卖销量时序时序数据的周期性可以设置为7天，某地区降雨量时序数据的周期性可以设置为1年，等等等等。

一个好的建议是基于你自己的领域经验来设置这个周期窗口。

3. 基于STL分解得到的残差信号进行异常离群点检测

对于时序数据来说，趋势信号和周期信号是需要过滤去除的部分，余下的残差信号才是做异常检测的数据源。

对残差信号的异常检测是以周期窗口为单位的，在每一个定长的周期窗口内，对时序信号的指标进行异常检测（假设检验或无监督异常检测）

4. 基于STL时序预测的异常检测

可以基于对历史数据的拟合，对未来的时序指标进行预测，将预测的结果作为一个基线。当未来的时序指标发生时，将其和基线进行对比，通过度量偏离程度，以此判断是否是异常离群点。 

0x3：基于STL时序分解算法的时序异常检测在SSH异常登录行为检测里的应用

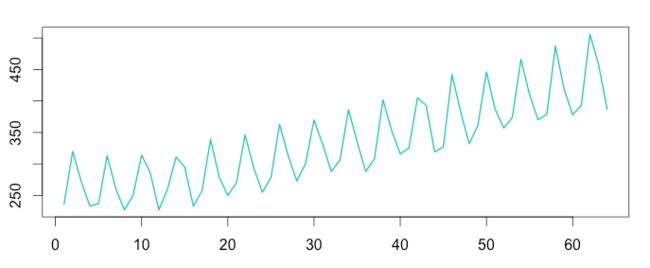
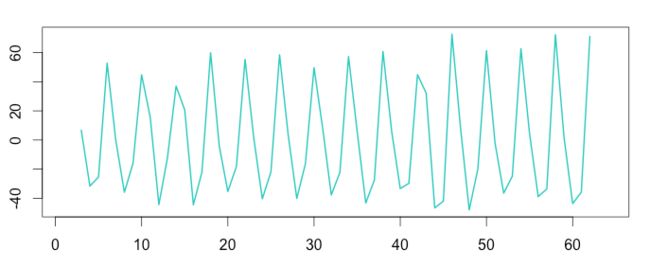
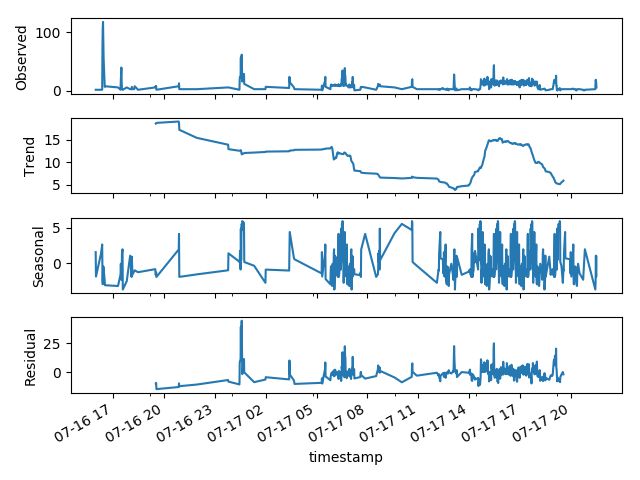
笔者这里拉取了某台网站服务器一段时间内的ssh登录时序流水记录，通过STL进行了分解，x轴为分钟时序，纵轴为每分钟内登录次数。

 

周期窗口配置为60min

如果我们将周期窗口拉长，时序数据中的周期性强度会降低，这本质上和STL的算法迭代过程有关，越长的周期窗口，周期信号被滑动平均的稀疏就越严重。

周期窗口配置为120mi

在STL的基础上，笔者对残差信号进行grubb's test假设检验异常检测。但是实验的结果并不理想。

这也反过来说明了ssh/rdp登录日志并不具备明显的时序周期性。

更一般地说，时序异常检测要求待检测的数据源本身就具备“时间密集性”，即不发生异常时，数据源本身就是一个包含周期性信号的密集时序信号，例如网站日常pv访问，4层数据包访问。

而时序中的异常定义，是说：某个时间点突发的突然性时序指标突变，或者整体时序周期性的水平平移异常（这种比较多），在业务场景中，占大多数的是前者，即某时刻时序指标的突变异常。

拿服务器的ssh/rdp登录日志来说，首先它是一个非时间密集型的时序数据，因为日常除了管理员之外，很少会有登录行为，如果一旦有大量登录行为，很可能就是有攻击者在对服务器进行爆破攻击。如果直接强行对ssh/rdp登录日志进行stl分解，得到的残差信号很可能就是攻击者的流量数据，基于这份残差数据对假设检验得到的异常时间点，本身也没有可解释性，很可能只是当时攻击者增加了攻击机器或者增加了网络带宽而已。

所以，ssh/rdp登录时序检测这个场景本身就不符合时序信号的基本假设，。

Relevant Link: 

https://juejin.im/post/5c19f4cb518825678a7bad4c
https://github.com/twitter/AnomalyDetection
https://mp.weixin.qq.com/s/w7SbAHxZsmHqFtTG8ZAXNg