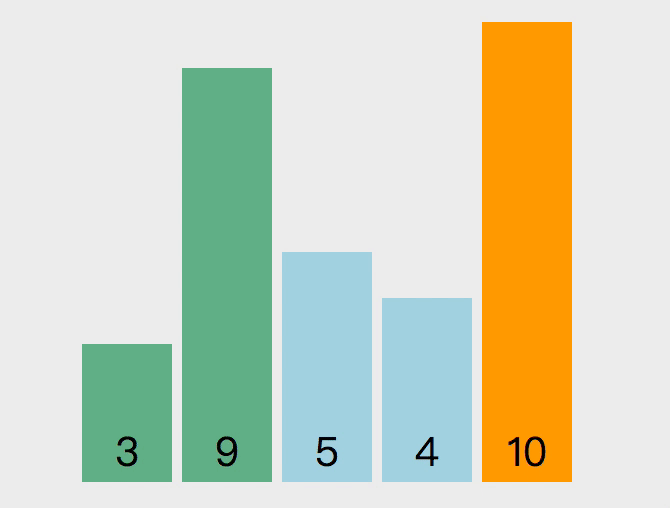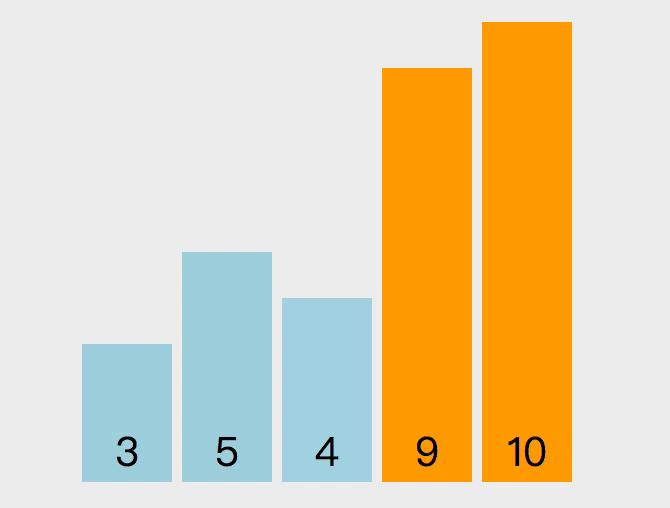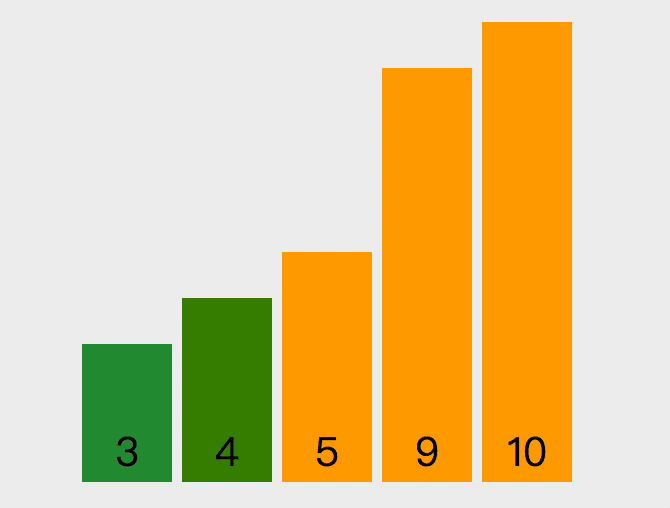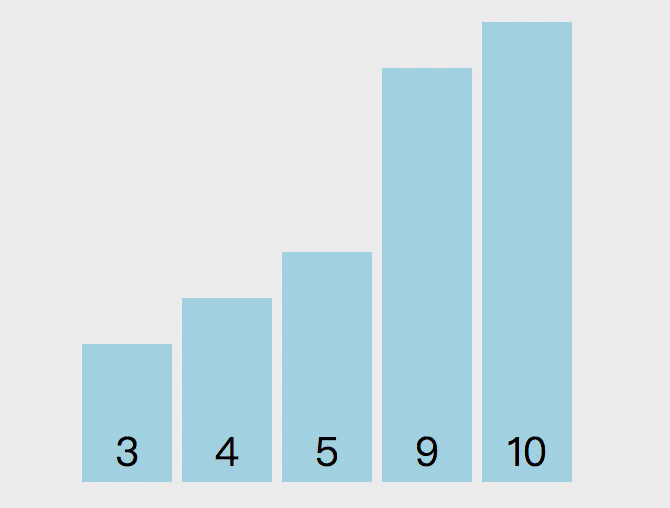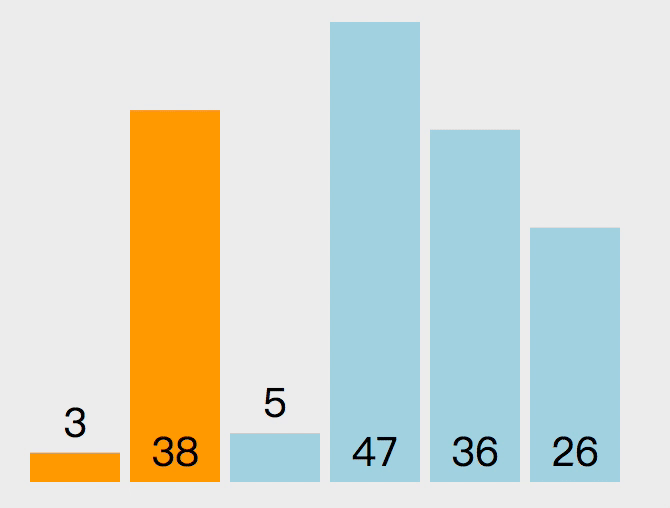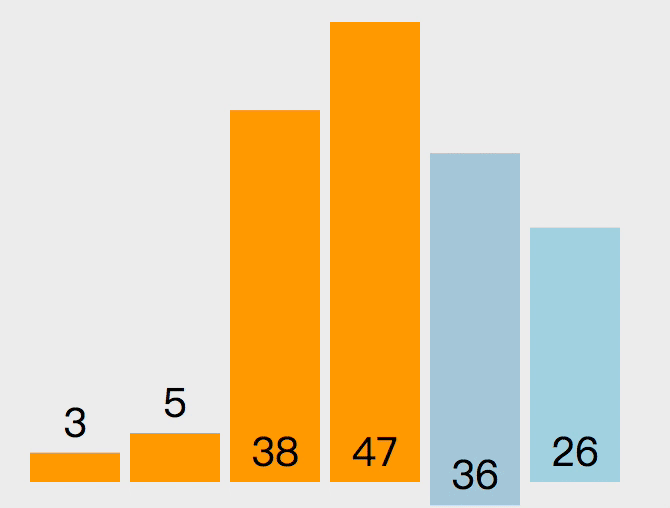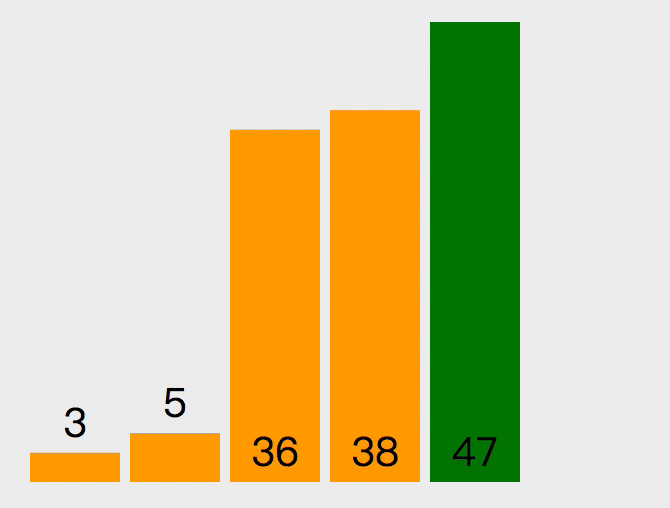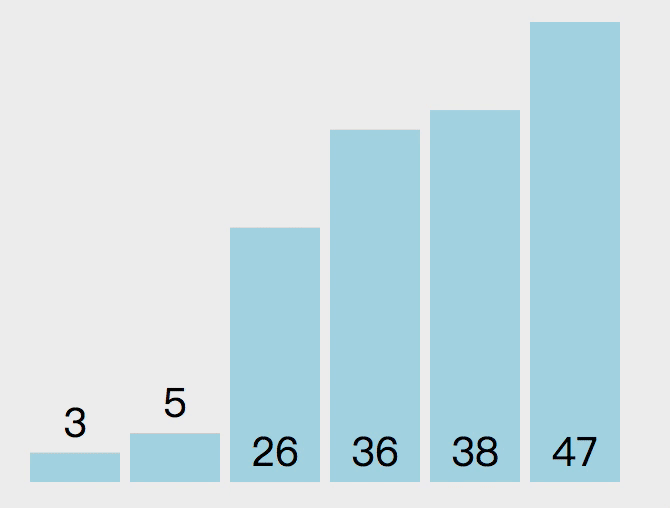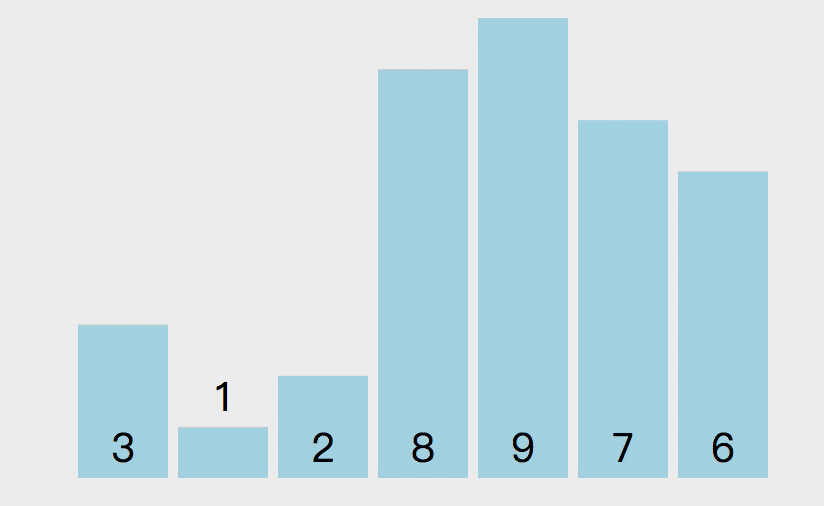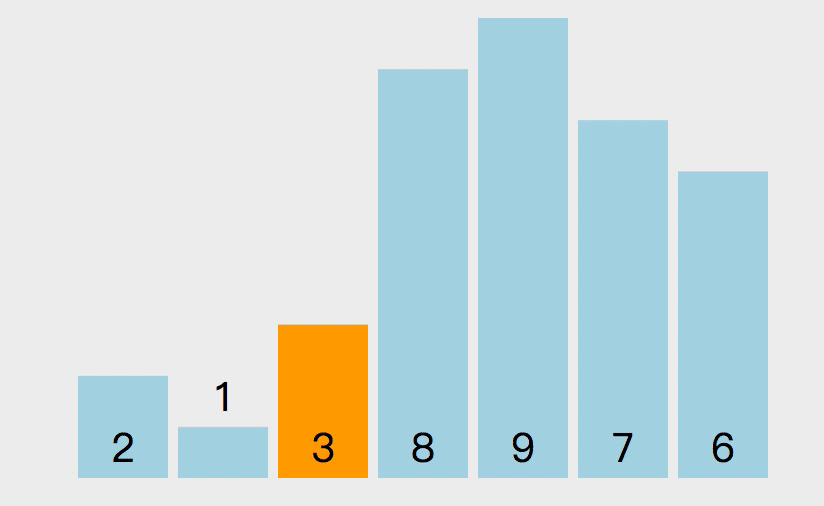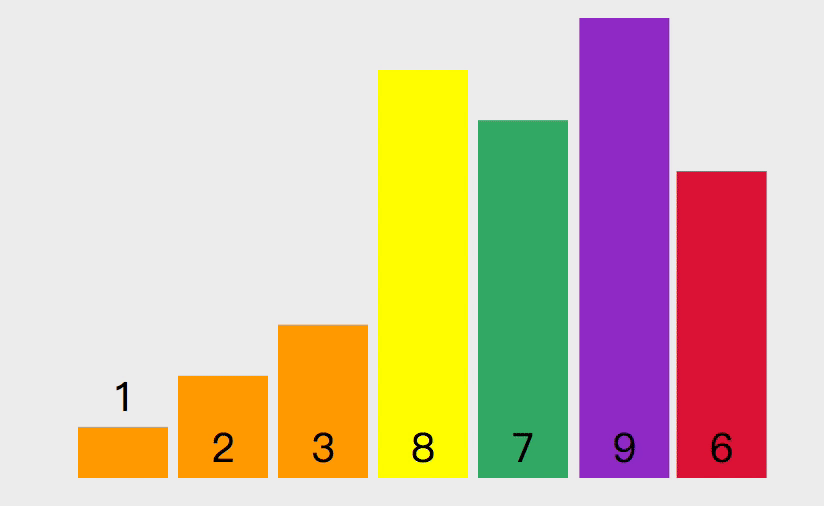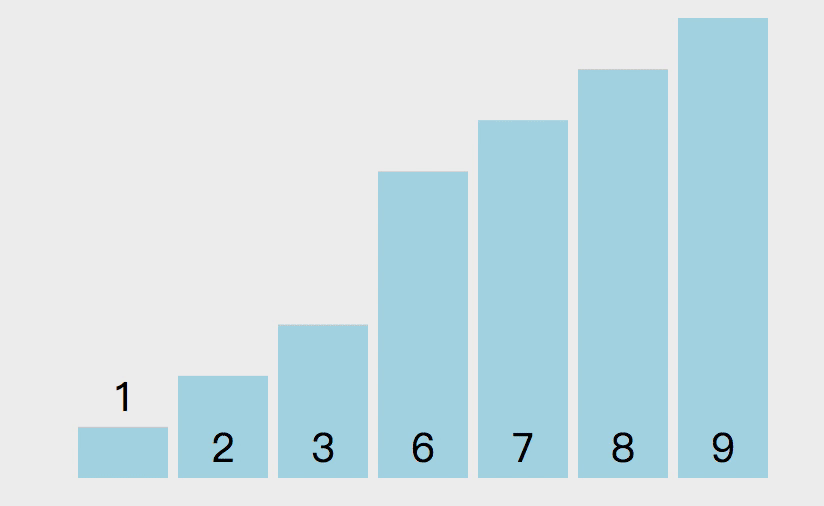数据结构算法-JavaScript常用排序法（常用排序方法的总结）

JavaScript常见排序

以下两个函数是排序中会用到的通用函数，就不一一写了

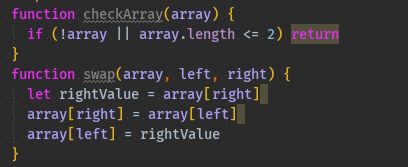
function checkArray(array) {
    if (!array || array.length <= 2) return
}
function swap(array, left, right) {
    let rightValue = array[right]
    array[right] = array[left]
    array[left] = rightValue
}

View Code

冒泡排序

冒泡排序的原理如下，从第一个元素开始，把当前元素和下一个索引元素进行比较。如果当前元素大，那么就交换位置，重复操作直到比较到最后一个元素，那么此时最后一个元素就是该数组中最大的数。下一轮重复以上操作，但是此时最后一个元素已经是最大数了，所以不需要再比较最后一个元素，只需要比较到 length - 1 的位置。

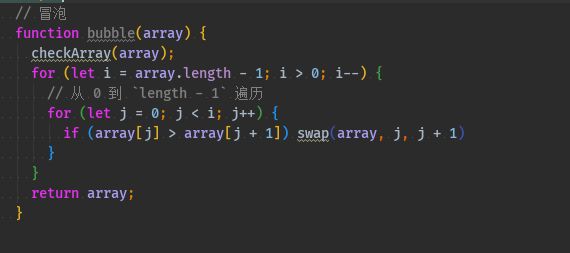
 以下是实现该算法的代码

function bubble(array) {
  checkArray(array);
  for (let i = array.length - 1; i > 0; i--) {
    // 从 0 到 `length - 1` 遍历
    for (let j = 0; j < i; j++) {
      if (array[j] > array[j + 1]) swap(array, j, j + 1)
    }
  }
  return array;
}

冒泡排序法

 该算法的操作次数是一个等差数列 n + (n - 1) + (n - 2) + 1 ，去掉常数项以后得出时间复杂度是 O(n * n)

插入排序

插入排序的原理如下。第一个元素默认是已排序元素，取出下一个元素和当前元素比较，如果当前元素大就交换位置。那么此时第一个元素就是当前的最小数，所以下次取出操作从第三个元素开始，向前对比，重复之前的操作。

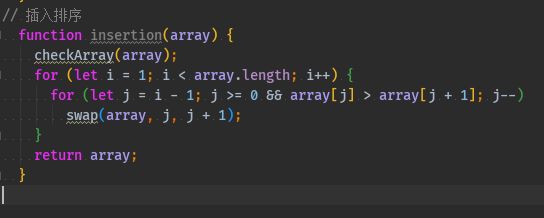
 以下是实现该算法的代码

function insertion(array) {
  checkArray(array);
  for (let i = 1; i < array.length; i++) {
    for (let j = i - 1; j >= 0 && array[j] > array[j + 1]; j--)
      swap(array, j, j + 1);
  }
  return array;
}

插入排序法

 该算法的操作次数是一个等差数列 n + (n - 1) + (n - 2) + 1 ，去掉常数项以后得出时间复杂度是 O(n * n)

选择排序

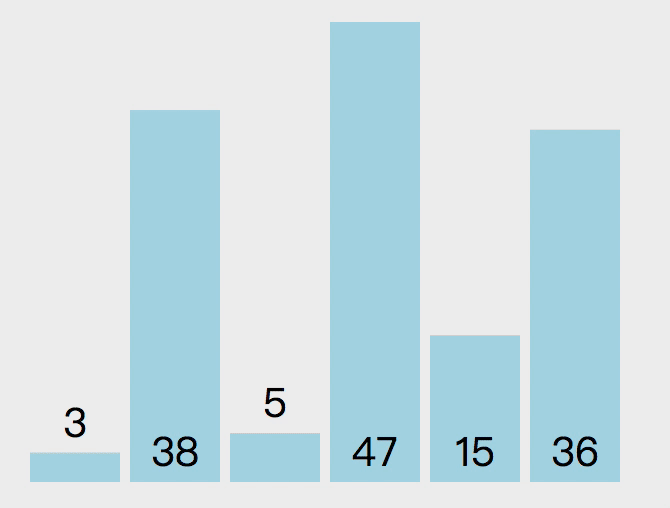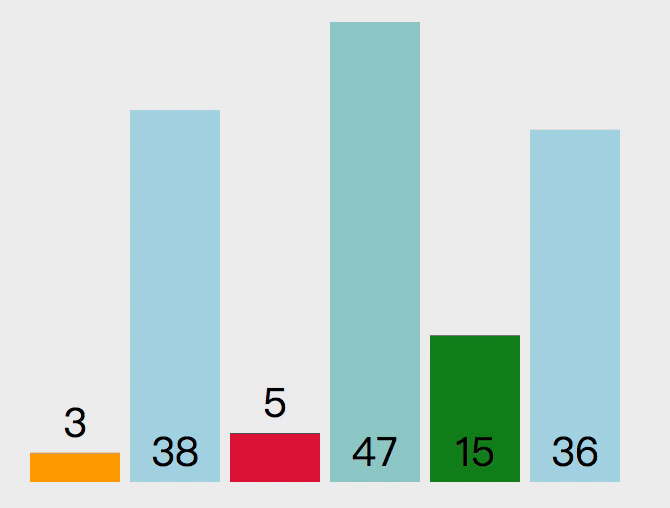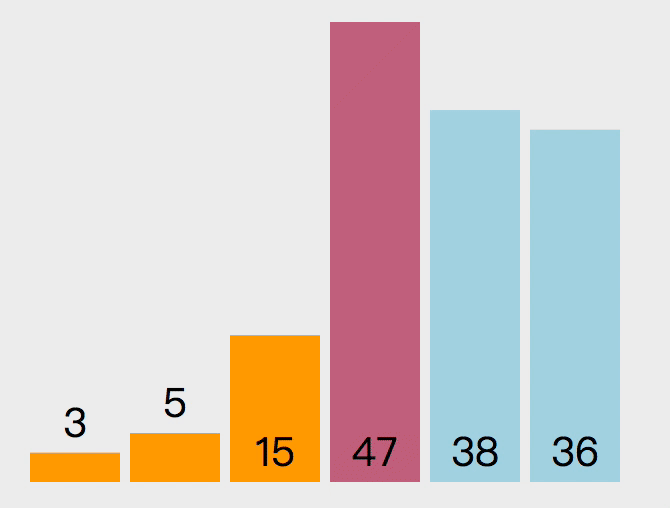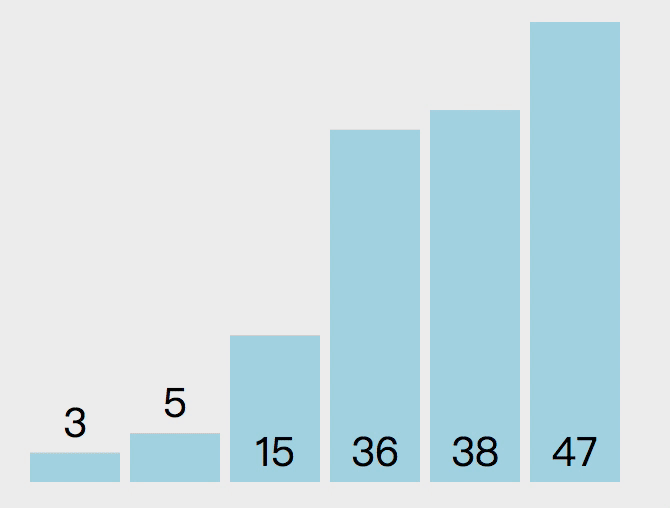
选择排序的原理如下。遍历数组，设置最小值的索引为 0，如果取出的值比当前最小值小，就替换最小值索引，遍历完成后，将第一个元素和最小值索引上的值交换。如上操作后，第一个元素就是数组中的最小值，下次遍历就可以从索引 1 开始重复上述操作。

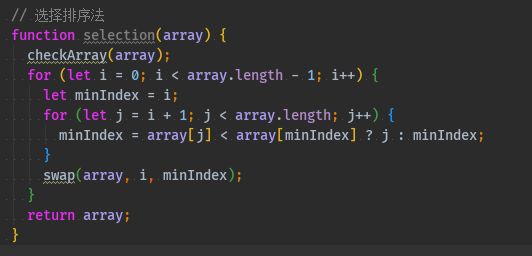
 以下是实现该算法的代码

function selection(array) {
  checkArray(array);
  for (let i = 0; i < array.length - 1; i++) {
    let minIndex = i;
    for (let j = i + 1; j < array.length; j++) {
      minIndex = array[j] < array[minIndex] ? j : minIndex;
    }
    swap(array, i, minIndex);
  }
  return array;
}

选择排序法

该算法的操作次数是一个等差数列 n + (n - 1) + (n - 2) + 1 ，去掉常数项以后得出时间复杂度是 O(n * n)

归并排序

归并排序的原理如下。递归的将数组两两分开直到最多包含两个元素，然后将数组排序合并，最终合并为排序好的数组。假设我有一组数组 [3, 1, 2, 8, 9, 7, 6]，中间数索引是 3，先排序数组 [3, 1, 2, 8] 。在这个左边数组上，继续拆分直到变成数组包含两个元素（如果数组长度是奇数的话，会有一个拆分数组只包含一个元素）。然后排序数组 [3, 1] 和 [2, 8] ，然后再排序数组 [1, 3, 2, 8] ，这样左边数组就排序完成，然后按照以上思路排序右边数组，最后将数组 [1, 2, 3, 8] 和 [6, 7, 9] 排序。

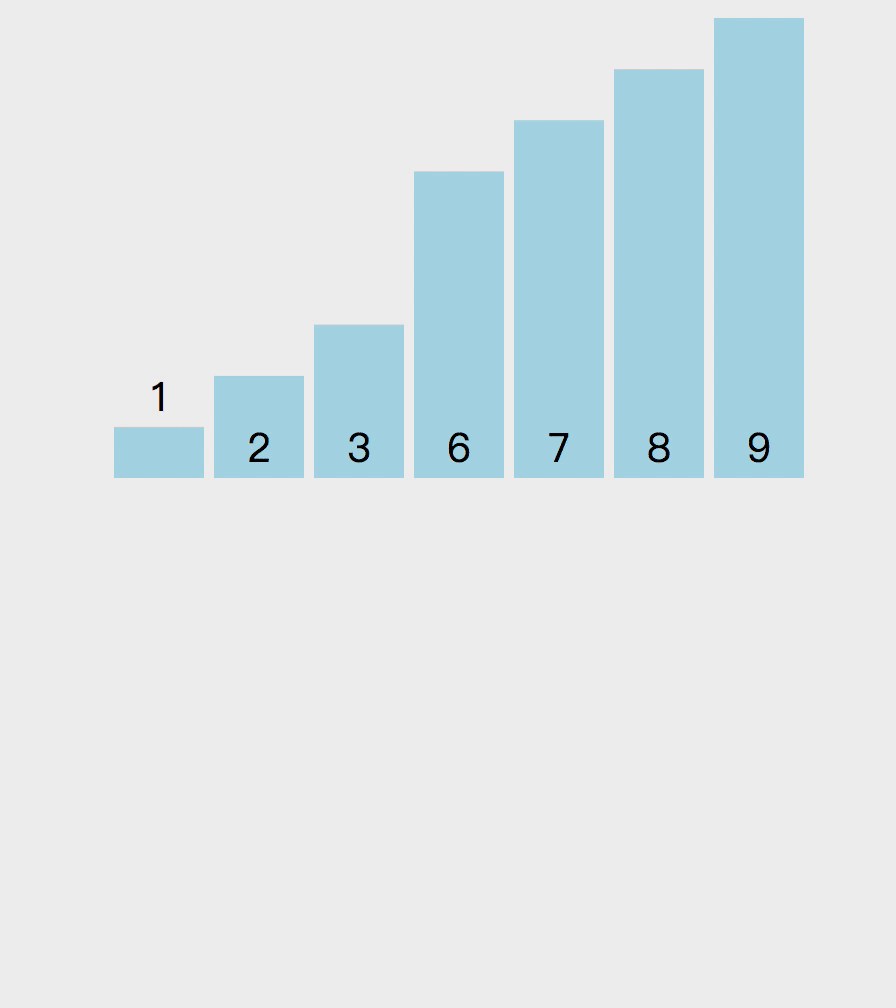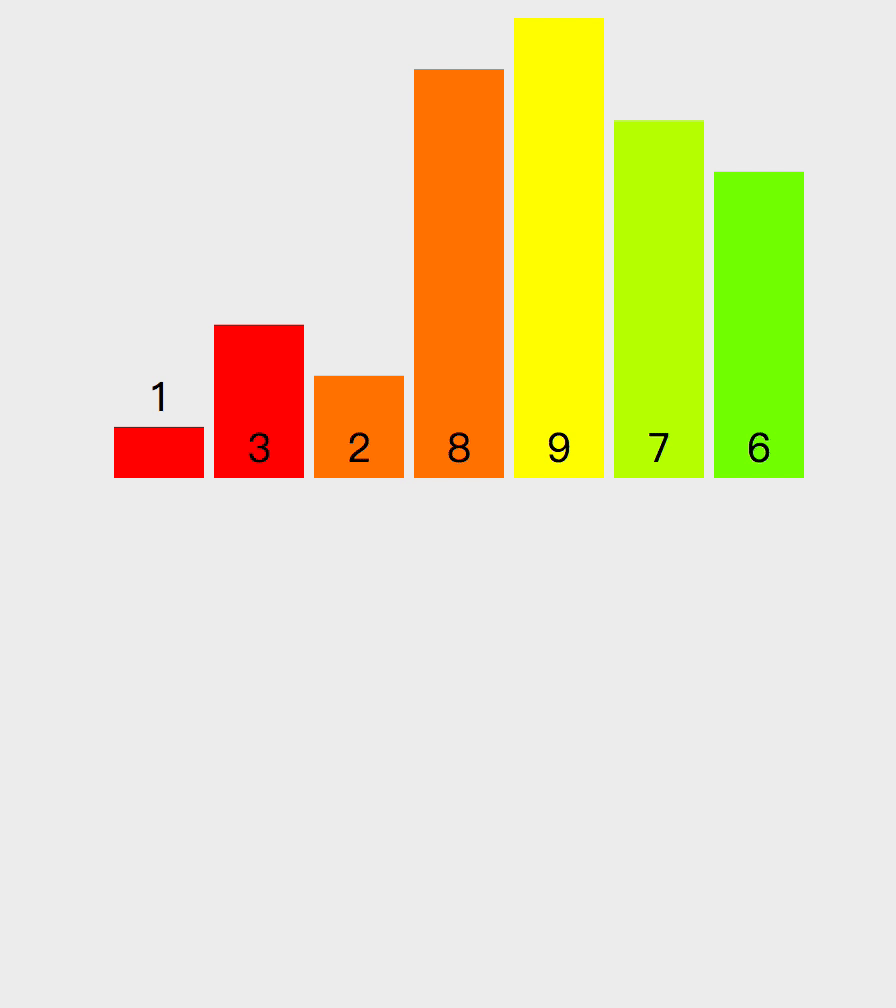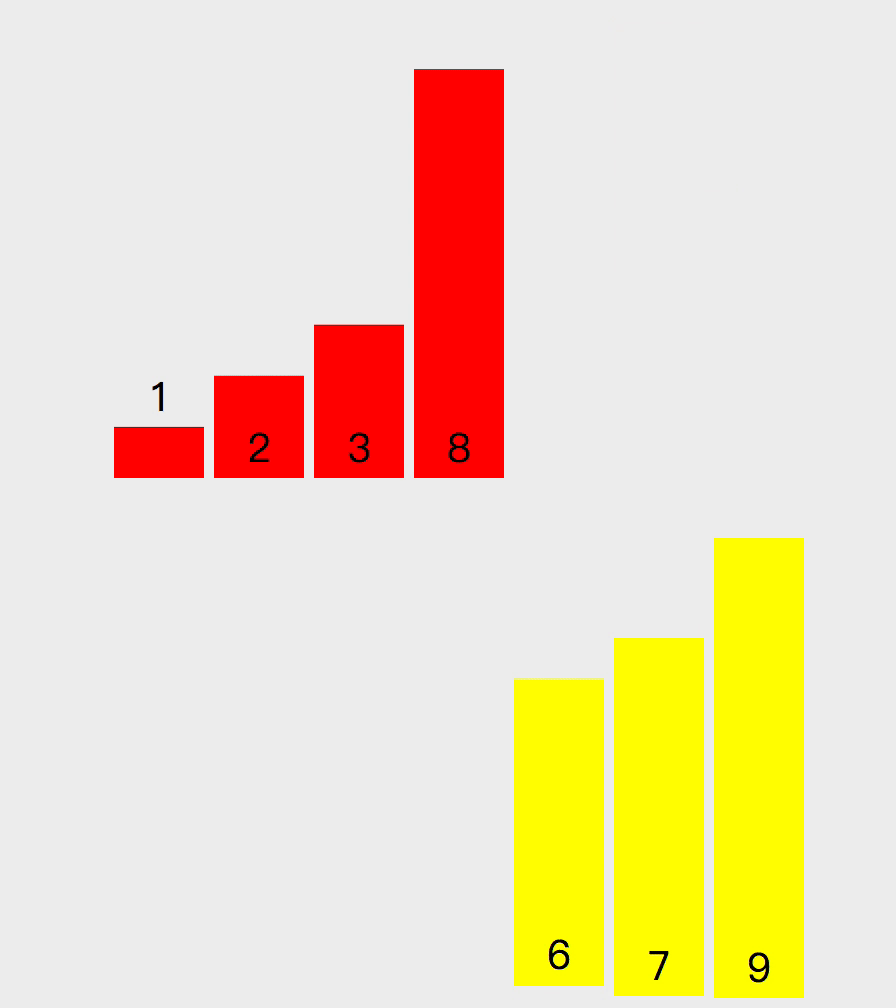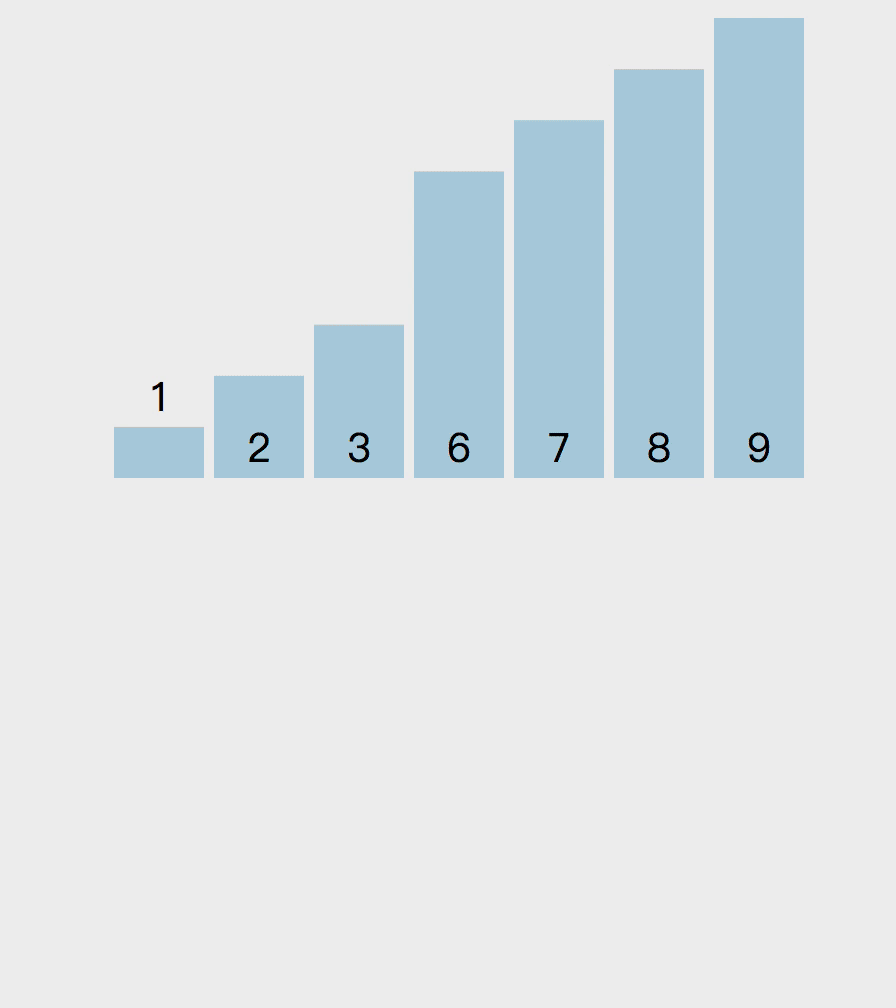
以下是实现该算法的代码

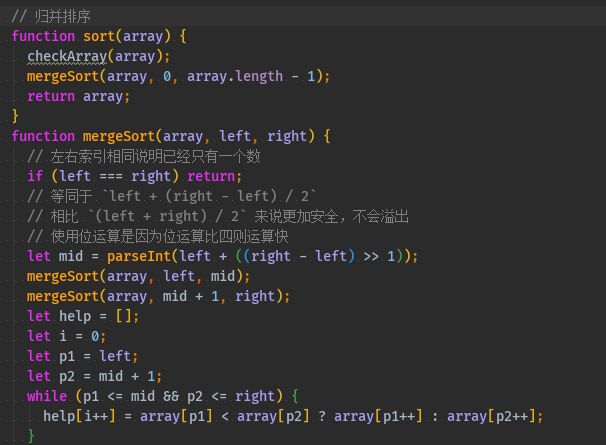
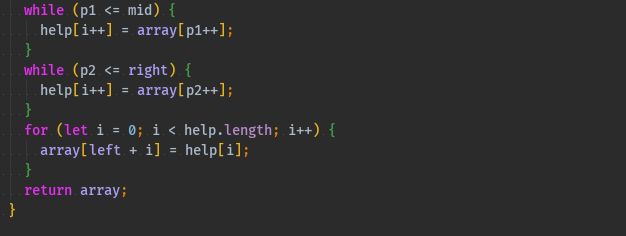
function sort(array) {
  checkArray(array);
  mergeSort(array, 0, array.length - 1);
  return array;
}

function mergeSort(array, left, right) {
  // 左右索引相同说明已经只有一个数
  if (left === right) return;
  // 等同于 `left + (right - left) / 2`
  // 相比 `(left + right) / 2` 来说更加安全，不会溢出
  // 使用位运算是因为位运算比四则运算快
  let mid = parseInt(left + ((right - left) >> 1));
  mergeSort(array, left, mid);
  mergeSort(array, mid + 1, right);

  let help = [];
  let i = 0;
  let p1 = left;
  let p2 = mid + 1;
  while (p1 <= mid && p2 <= right) {
    help[i++] = array[p1] < array[p2] ? array[p1++] : array[p2++];
  }
  while (p1 <= mid) {
    help[i++] = array[p1++];
  }
  while (p2 <= right) {
    help[i++] = array[p2++];
  }
  for (let i = 0; i < help.length; i++) {
    array[left + i] = help[i];
  }
  return array;
}

归并排序法

 

 以上算法使用了递归的思想。递归的本质就是压栈，每递归执行一次函数，就将该函数的信息（比如参数，内部的变量，执行到的行数）压栈，直到遇到终止条件，然后出栈并继续执行函数。对于以上递归函数的调用轨迹如下

mergeSort(data, 0, 6) // mid = 3
  mergeSort(data, 0, 3) // mid = 1
    mergeSort(data, 0, 1) // mid = 0
      mergeSort(data, 0, 0) // 遇到终止，回退到上一步
    mergeSort(data, 1, 1) // 遇到终止，回退到上一步
    // 排序 p1 = 0, p2 = mid + 1 = 1
    // 回退到 `mergeSort(data, 0, 3)` 执行下一个递归
  mergeSort(2, 3) // mid = 2
    mergeSort(3, 3) // 遇到终止，回退到上一步
  // 排序 p1 = 2, p2 = mid + 1 = 3
  // 回退到 `mergeSort(data, 0, 3)` 执行合并逻辑
  // 排序 p1 = 0, p2 = mid + 1 = 2
  // 执行完毕回退
  // 左边数组排序完毕，右边也是如上轨迹

View Code

 该算法的操作次数是可以这样计算：递归了两次，每次数据量是数组的一半，并且最后把整个数组迭代了一次，所以得出表达式 2T(N / 2) + T(N) （T 代表时间，N 代表数据量）。根据该表达式可以套用 该公式 得出时间复杂度为 O(N * logN)

快排

快排的原理如下。随机选取一个数组中的值作为基准值，从左至右取值与基准值对比大小。比基准值小的放数组左边，大的放右边，对比完成后将基准值和第一个比基准值大的值交换位置。然后将数组以基准值的位置分为两部分，继续递归以上操作。

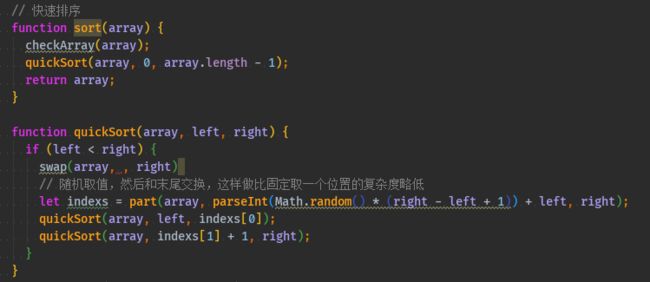
 以下是实现该算法的代码

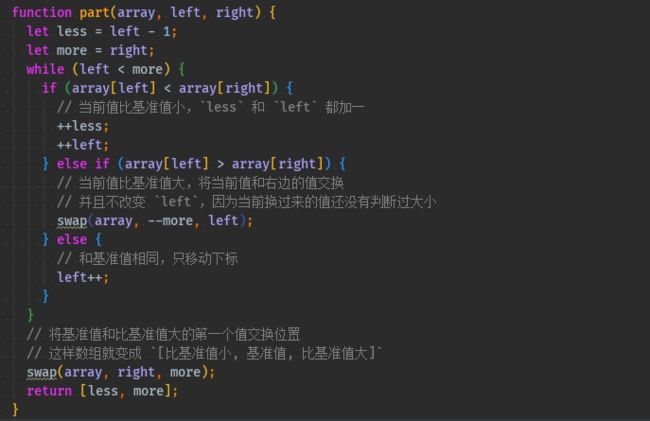
function sort(array) {
  checkArray(array);
  quickSort(array, 0, array.length - 1);
  return array;
}

function quickSort(array, left, right) {
  if (left < right) {
    swap(array, , right)
    // 随机取值，然后和末尾交换，这样做比固定取一个位置的复杂度略低
    let indexs = part(array, parseInt(Math.random() * (right - left + 1)) + left, right);
    quickSort(array, left, indexs[0]);
    quickSort(array, indexs[1] + 1, right);
  }
}
function part(array, left, right) {
  let less = left - 1;
  let more = right;
  while (left < more) {
    if (array[left] < array[right]) {
      // 当前值比基准值小，`less` 和 `left` 都加一
       ++less;
       ++left;
    } else if (array[left] > array[right]) {
      // 当前值比基准值大，将当前值和右边的值交换
      // 并且不改变 `left`，因为当前换过来的值还没有判断过大小
      swap(array, --more, left);
    } else {
      // 和基准值相同，只移动下标
      left++;
    }
  }
  // 将基准值和比基准值大的第一个值交换位置
  // 这样数组就变成 `[比基准值小, 基准值, 比基准值大]`
  swap(array, right, more);
  return [less, more];
}

快速排序法

 

 该算法的复杂度和归并排序是相同的，但是额外空间复杂度比归并排序少，只需 O(logN)，并且相比归并排序来说，所需的常数时间也更少。

堆排序

堆排序利用了二叉堆的特性来做，二叉堆通常用数组表示，并且二叉堆是一颗完全二叉树（所有叶节点（最底层的节点）都是从左往右顺序排序，并且其他层的节点都是满的）。二叉堆又分为大根堆与小根堆。

• 大根堆是某个节点的所有子节点的值都比他小
• 小根堆是某个节点的所有子节点的值都比他大

堆排序的原理就是组成一个大根堆或者小根堆。以小根堆为例，某个节点的左边子节点索引是 i * 2 + 1，右边是 i * 2 + 2，父节点是 (i - 1) /2。

1. 首先遍历数组，判断该节点的父节点是否比他小，如果小就交换位置并继续判断，直到他的父节点比他大
2. 重新以上操作 1，直到数组首位是最大值
3. 然后将首位和末尾交换位置并将数组长度减一，表示数组末尾已是最大值，不需要再比较大小
4. 对比左右节点哪个大，然后记住大的节点的索引并且和父节点对比大小，如果子节点大就交换位置
5. 重复以上操作 3 - 4 直到整个数组都是大根堆。

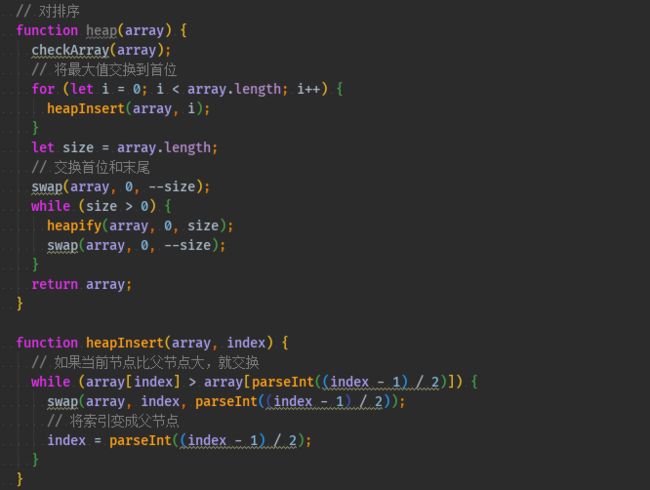
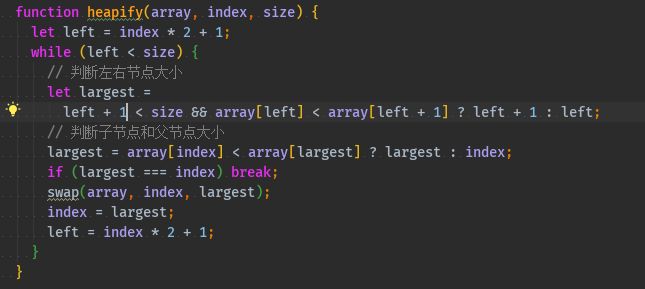
以下是实现该算法的代码

function heap(array) {
  checkArray(array);
  // 将最大值交换到首位
  for (let i = 0; i < array.length; i++) {
    heapInsert(array, i);
  }
  let size = array.length;
  // 交换首位和末尾
  swap(array, 0, --size);
  while (size > 0) {
    heapify(array, 0, size);
    swap(array, 0, --size);
  }
  return array;
}

function heapInsert(array, index) {
  // 如果当前节点比父节点大，就交换
  while (array[index] > array[parseInt((index - 1) / 2)]) {
    swap(array, index, parseInt((index - 1) / 2));
    // 将索引变成父节点
    index = parseInt((index - 1) / 2);
  }
}
function heapify(array, index, size) {
  let left = index * 2 + 1;
  while (left < size) {
    // 判断左右节点大小
    let largest =
      left + 1 < size && array[left] < array[left + 1] ? left + 1 : left;
    // 判断子节点和父节点大小
    largest = array[index] < array[largest] ? largest : index;
    if (largest === index) break;
    swap(array, index, largest);
    index = largest;
    left = index * 2 + 1;
  }
}

对排序法

 

以上代码实现了小根堆，如果需要实现大根堆，只需要把节点对比反一下就好。
该算法的复杂度是 O(logN)

 

 

 

参考总结资料：https://juejin.im/post/5ba34e54e51d450e5162789b#heading-87