本文对9种排序方法进行汇总。
分别是: 插入排序 选择排序 归并排序 冒泡排序 堆排序 快排序 计数排序 基数排序 桶排序。
参照《算法》第四版这本书,把排序需要的公共的方法抽象出来,做一个抽象类,讨论到的各个排序类对抽象类进行继承,只需关注与排序本身的业务逻辑即可。
https://visualgo.net/sorting
抽象出来的父类为:
abstract Sort{
abstract void sort(array); // 需要被实现
void exchange(array, i, j); // 交换数组中的i 和j位置的元素
boolean less(a, b); // a是否小于b
boolean isSorted(array); // 数组是否已排好序
void test(arr); // 对传入的数组进行测试
}对应的Java实现
/**
1. 排序的抽象类
2. 可以接受任意类型,可以自定义比较器
3. @param
*/
public abstract class Sort {
/** 测试数组,这里为了方便使用整型数组*/
protected static Integer[] testArray = { 3, 2, 5, 1, 4, 7 ,10};
/** 继承该类需要实现排序方法*/
public abstract void sort(Comparable[] array);
/** 交换数组元素的业务方法*/
protected void exchange(Comparable[] array, int i, int j){
Comparable temp = array[i];
array[i] = array[j];
array[j] = temp;
}
/** 比较两个元素的方法*/
protected boolean less(Comparable a, Comparable b){
return a.compareTo((T) b) < 0;
}
/** 判断数组是否已排序的方法*/
protected boolean isSorted(Comparable[] array){
for(int i = 1; i[] arr){
//输出排序前的数组
System.out.println(Arrays.toString(arr));
//排序
sort(arr);
//输出排序后的结果
System.out.println(Arrays.toString(arr));
//输出是否已经排序
System.out.println("是否已经排序:" + isSorted(arr));
}
} 1.插入排序
时间O(n^2);空间O(1);
排序时间与输入有关:输入的元素个数,输入元素已排序程度;
最好情况:输入数组已经是排序的,时间变为n的线性函数;
最坏情况:输入数组是逆序,时间是n的二次函数
/**
* 插入排序
*/
public class InsertSort extends Sort {
@Override
public void sort(Comparable[] array) {
int len = array.length;
// 把a[i] 插入到a[i-1], a[i-2], a[i-3]...中
for (int i = 1; i < len; i++) {
// j从i开始,如果j>0并且j处元素比前面的元素小,则进行交换,j--,继续向前比较
for (int j = i; j > 0 && less(array[j], array[j-1]); j--)
exchange(array, j, j-1);
}
}
public static void main(String[] args) {
new InsertSort().test(testArray);
}
} 结果:
[3, 2, 5, 1, 4, 7, 10]
[1, 2, 3, 4, 5, 7, 10]
是否已经排序:true
2.选择排序
时间O(n^2),空间O(1)
排序时间和输入无关
最好和最坏都是一样的
不稳定,例如{6, 6, 1}.找到最小的是1,和第一个6交换以后,第一个6跑到了后面.
/**
* 选择排序
*/
public class SelectionSort extends Sort{
@Override
public void sort(Comparable[] array) {
int len = array.length;
for(int i = 0; i 3.归并排序
归并排序的所有算法都基于归并这个简单的操作,即将两个有序的数组归并称为一个更大的有序数组。
发现这个算法的由来:要将一个数组排序,可以先递归地将它分成两半分别排序,然后将结果归并起来。
性质:能够保证将任意长度为N的数组排序,所需时间和NlogN成正比;
缺点:所需额外空间和N成正比。
3.1自顶向下的归并排序算法
/**
* 归并排序:自顶向下
* 分治思想的最经典的一个例子。
* 这段递归代码是归纳证明算法能够正确地将数组排序的基础:
* 如果它能将两个子数组排序,它就能通过归并两个子数组来讲整个数组排序
*/
public class MergeSort extends Sort{
private static Comparable[] auxiliary;
@Override
public void sort(Comparable[] array) {
auxiliary = new Comparable[array.length];
sort(array, 0, array.length-1);
}
private void sort(Comparable[] array, int low, int high) {
if(high <= low) return;
int mid = low + (high - low) / 2;
sort(array, low, mid); //将左半边排序
sort(array, mid + 1, high); //将右半边排序
merge(array, low, mid, high);//归并结果
}
private void merge(Comparable[] a, int low, int mid, int high){
// 将a[low...mid]和a[mid+1...high]归并
int i = low, j = mid + 1;
// 先将所有元素复制到aux中,然后再归并会a中。
for(int k = low; k <= high; k++)
auxiliary[k] = a[k];
for(int k = low; k <= high; k++)//归并回到a[low...high]
if(i > mid)
a[k] = auxiliary[j++]; // 左半边用尽,取右半边的元素
else if (j > high)
a[k] = auxiliary[i++]; // 右半边用尽,取左半边的元素
else if (less(auxiliary[j], auxiliary[i]))
a[k] = auxiliary[j++]; // 右半边当前元素小于左半边当前元素,取右半边的元素
else
a[k] = auxiliary[i++]; // 左半边当前元素小于又半边当前元素,取左半边的元素
}
public static void main(String[] args) {
new MergeSort().test(testArray);
}
} 这个NLogN的时间复杂度和插入排序和选择排序不可同日而语,它表明只需比遍历整个数组多个对数因子的时间就能将一个庞大的数组排序。可以用归并排序处理百万甚至更大规模的数组,这是插入和选择排序所做不到的。
其缺点是辅助数组所使用的额外空间和N的大小成正比。
另外通过一些细致的思考,还可以大幅度缩短归并排序的运行时间。
考虑1:对小规模子数组使用插入排序。使用插入排序处理小规模的子数组(比如长度小于15)一般可以将归并排序运行时间缩短10%-15%。
考虑2:测试数组是否已经有序。可以添加一个判断条件,如果array[ mid ] <= array[ mid + 1 ]就认为数组已经是有序的,并跳过merge方法,这个改动不影响排序的递归调用,但是任意有序的子数组算法运行的时间就变成线性了。
考虑3:不将元素复制到辅助数组。可以节省将元素复制到用于归并的辅助数组所用的时间(但空间不行)。要做到这一点需要调用两种排序方法,一种将数据从输入属猪排序到辅助数组,一种将数据从辅助数组排序到输入数组。
3.2 自底向上的归并排序
先归并那些微型数组,然后再成对归并得到的子数组,如此这般,直到将整个数组归并在一起。
该实现比标准递归方法代码量少。
首先进行两两归并,然后四四归并,八八归并,一直下去。在每一轮归并中,最后一次归并的第二个子数组可能比第一个要小,但是对merge方法不是问题,如果不是的话所有的归并中两个数组的大小都应该一样,而在下一轮中子数组的大小翻倍。如图:
/**
* 自底向上的归并排序
* 会多次遍历整个数组,根据子数组大小进行两两归并。
* 子数组的大小size初始值为1,每次加倍。
* 最后一个子数组的大小只有在数组大小是size的偶数被时才会等于size,否则会比size小。
* @param
*/
public class MergeSortBU extends Sort{
private static Comparable[] aux;
@Override
public void sort(Comparable[] a) {
int n = a.length;
aux = new Comparable[n];
//进行lgN次两两归并
for(int size = 1; size < n; size = size + size)
for(int low = 0; low < n - size; low += size+size)
merge(a, low, low+size-1, Math.min(low+size + size-1, n-1));
}
@SuppressWarnings("unchecked")
private void merge(Comparable[] a, int low, int mid, int high){
int i = low, j = mid + 1;
for(int k = low; k <= high; k++)
aux[k] = a[k];
for(int k = low; k <= high; k++){
if(i > mid)
a[k] = aux[j++];
else if(j > high)
a[k] = aux[i++];
else if(less(a[j], a[i]))
a[k] = aux[j++];
else
a[k] = aux[i++];
}
}
public static void main(String[] args) {
new MergeSortBU().test(testArray);
}
} 4.冒泡排序
比较简单
/**
* 冒泡排序
* 时间:O(n^2);空间O(1)
* 稳定,因为存在两两比较,不存在跳跃
* 排序时间与输入无关
*/
public class BubbleSort extends Sort {
@Override
public void sort(Comparable[] array) {
int len = array.length;
for(int i = 0; ii; j--){
if(less(array[j], array[j-1]))
exchange(array, j, j-1);
}
}
}
public static void main(String[] args) {
new BubbleSort().test(testArray);
}
} 缺陷:
排序过程中,执行完第i趟排序后,可能数据已全部排序完毕,但是程序无法判断是否完成排序,会继续执行剩下的(n-1-i)趟排序。解决方法:设置一个flag位,如果一趟无元素交换,则flag=0;以后再也不进入第二层循环。
当排序的数据比较多时,排序的时间会明显延长,因为会比较n*(n-1)/2次。
5. 快排序
快排序
实现简单,适用于各种不同输入,一般应用中比其他算法快很多。
特点:原地排序(只需很小的一个辅助栈);时间和NlgN成正比。同时具备这两个优点。
另外,快排序的内循环比大多数排序算法都短。5.1 基本算法
快排序是一种分治的算法,将一个数组分成两个子数组,将两部分独立排序。
快排序和归并排序互补:归并排序将数组分成两个子数组分别排序,并将有序的子数组归并以将整个数组排序;
而快排序将数组排序的方式是当两个子数组都有序的时候,整个数组自然也就有序了。
第一种情况,递归调用发生在处理整个数组之前;第二种情况,递归发生在处理整个数组之后。
归并排序中,一个数组被等分为两半;快排序中,切分的位置取决于数组的内容。
/**
* 快排序
*/
public class QuickSort extends Sort {
@Override
public void sort(Comparable[] array) {
shuffle(array);
System.out.println("打乱后:"+Arrays.toString(array));
sort(array, 0, array.length - 1);
}
private void sort(Comparable[] array, int low, int high) {
if(high <= low) return;
int j = partition(array, low, high); // 切分
sort(array, low, j-1); // 将左半部分array[low, ... , j-1]进行排序
sort(array, j+1, high); // 将右半部分array[j+1, ... , high]进行排序
}
private int partition(Comparable[] array, int low, int high) {
// 将数组切分为array[low, ... , i-1], array[i], array[i+1, ... , high]
int i = low, j = high+1; //左右扫描指针
Comparable v = array[low];
while(true){
//扫描左右,检查扫描是否结束并交换元素
while(less(array[++i], v)) if(i == high) break;//左指针向右找到一个大于v的位置
while(less(v, array[--j])) if(j == low) break;//右指针向左找到一个小于v的位置
if(i >= j) break; // 如果左指针重叠或者超过右指针,跳出
exchange(array, i, j); // 交换左右指针位置的元素
}
exchange(array, low, j);
return j;
}
private void shuffle(Comparable[] a){
Random random = new Random();
for(int i = 0; i().test(testArray);
}
} 这段代码按照array[low] 的值v进行切分。当指针i和j相遇时主循环退出。在循环中,array[i]小于v时,增大i,a[j]大于v时,减小j,然后交换array[i]和array[j]来保证i左侧的元素都不大于v,j右侧的元素都不小于v。当指针相遇时交换array[low]和array[j],切分结束,这样切分值就留在array[j]中了。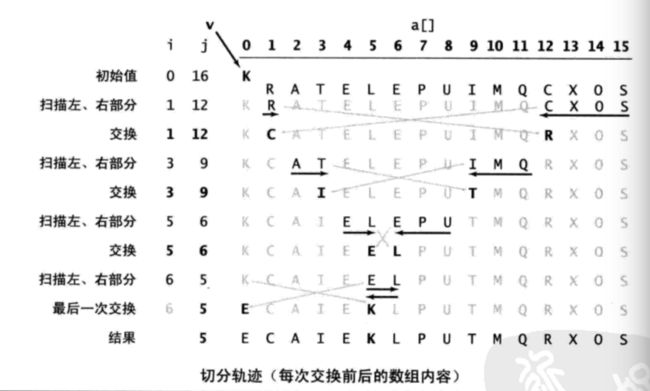
5.2快排序算法的改进:
如果排序代码会被执行很多次,或者会被用在大型数组上(特别是如果被发布成一个库函数,排序的对象数组的特性是未知的),那么需要提升性能。
以下改进会将性能提升20%~30%。
切换到插入排序
对于小数组,快排序比插入排序慢
因为递归,快排序的Sort方法在小数组中也会调用自己
基于这两点可以改进快排序。改动以上算法,将sort()方法中的语句
if(high <= low) return ;
替换为:
if(high <= low + M) { Insersion.sort(array, low, high); return; }
转换参数M的最佳值和系统相关,5~15之间的任意值在大多情况下都令人满足。
三取样切分
使用子数组的一小部分元素的中位数来切分数组。这样做得到的切分更好,但是代价是需要计算中位数。
发现将取样大小设置为3并用大小居中的元素切分的效果最好。
还可以将取样元素放到数组末尾作为哨兵来去掉partition()中的数组边界测试。
熵最优的排序
在有大量重复元素的情况下,快速排序的递归性会使元素全部重复的子数组经常出现,这样就有很大的改进潜力,能提高到线性级别。
简单的想法:将数组且分为3部分,分别对应小于,等于和大于切分元素的数组袁术。这种切分实现起来比目前的二分法更复杂。
/**
* 快排序:三项切分的快速排序
*/
public class Quick3WaySort extends Sort {
@Override
public void sort(Comparable[] array) {
shuffle(array);
System.out.println("打乱后:"+Arrays.toString(array));
sort(array, 0, array.length - 1);
}
private void sort(Comparable[] array, int low, int high) {
if(high <= low) return;
int lt = low, i = low + 1, gt = high;
Comparable v = array[low];
while(i <= gt){
int cmp = array[i].compareTo(v);
if(cmp < 0) exchange(array, lt++, i++);
else if(cmp > 0) exchange(array, i, gt--);
else i++;
} // 现在array[low ... lt-1] < v = a[lt ... gt] < array[gt+1 .. high]成立
sort(array, low, lt-1);
sort(array, gt+1, high);
}
private void shuffle(Comparable[] a){
Random random = new Random();
for(int i = 0; i().test(chars);
}
} 6.堆排序
时间复杂度O(nlogn), 空间复杂度O(1), 是一种原地排序。
排序时间和输入无关,不稳定。
对于大数据处理:如果对于100亿条数据选择 top K 的数据,只能用堆排序。堆排序只需要维护一个k大小的空间,即在内存开辟k大小的空间。
而不能选择快速排序,因为快排序要开辟1000亿条数据的空间,这个是不可能的。
这里先来看算法第四版这本书中的2.4节:优先级队列
应用举例:绝大多数手机分配给来电的优先级都会比其他应用高。
数据结构:优先级队列,需支持两种操作 删除最大元素和插入元素。
本节中简单讨论优先级队列的基本表现形式,其一或者两种操作都能在线性时间内完成。之后学习基于二叉堆结构的一中优先级队列的经典实现方法,
用数组保存元素并按照一定条件排序,以实现高效删除最大元素和插入元素的操作(对数级别)。
堆排序算法也来自于基于堆的优先级队列的实现。
稍后学习用优先级队列构造其他算法。
也能恰到好处的抽象若干重要的图搜索算法(算法第四版第四章)。
也可以开发出一种数据压缩算法(算法第四版第五章)。
三个构造函数使得用例可以构造制定大小的优先级队列,还可以用给定的一个数组将其初始化。
会在适当的地方使用另一个类MinPQ, 和MaxPQ类似,只是含有一个delMin()方法来删除并返回最小元素。
MaxPQ的任意实现都能很容易转化为MinPQ的实现,反之亦然,只需要改变一下less()比较的方向即可。
优先级队列的调用示例
为了展示优先级队列的价值,考虑问题:输入N个字符串,每个字符串都对应一个整数,找出最大的或最小的M个整数(及其关联的字符串)。
例如:输入金融事务,找出最大的那些;农产品中杀虫剂含量,找出最小的那些。。。
某些场景中,输入量可能是巨大的,甚至可以认为输入是无限的。
解决这个问题,
一种方法是将输入排序,然后从中找出M个最大元素。
另一种方法,将每个新的输入和已知的M个最大元素比较,但除非M较小,否则这种比较代价高昂。
使用优先级队列,这种才是正解,只要高效的实现insert和delMin方法即可。
三种方法的成本:
命令行输入一个整数M以及一系列字符串,每一行表示一个事务,代码调用MinPQ并打印数字最大的M行。
堆的定义:二叉堆能够很好的实现优先级队列的基本操作。
当一颗二叉树的每个结点都大于等于它的两个子结点时,被称为堆有序。
根节点是堆有序的二叉树中的最大节点。
二叉堆:一组能够用堆有序的完全二叉树排序的元素,并在数组中按层级存储(不使用数组的第0个位置)
在一个堆中,位置K的节点的父节点位置为 K/2 向下取整,两个子节点的位置分别是2K和2K+1。这样可以在不使用指针的情况下通过计算数组的索引在树中上下移动:从a[k]向上一层,就令k = k/2,向下一层就令k = 2k 或者2k+1。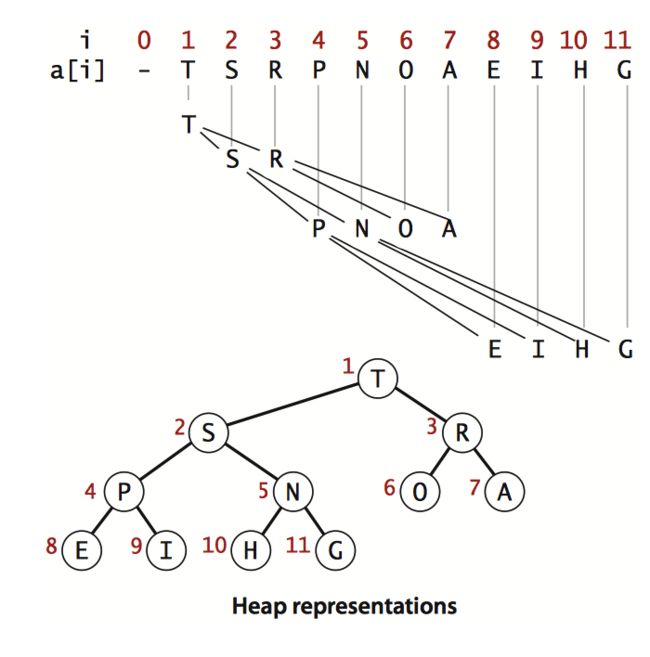
用数组实现的完全二叉树结构严格,但其灵活性足以让我们高效的实现优先级队列。
能够实现对数级别的插入元素和删除最大元素的操作。利用数组无需指针即可沿着树上下移动的遍历和以下性质,保证了对数复杂度的性能。
命题:一颗大小为N的完全二叉树的高度为lgN向下取整。
堆的算法:
用长度为N+1的私有数组pq[]来表示一个大小为N的堆,不使用pq[0],对元素放在pq[1]—pq[n]中。
在之前的排序中,通过辅助函数less和exchange函数来访问元素,但因为所有的元素都在数组pq中,该实现为了更加紧凑,不再将数组作为参数传递。
堆的操作首先进行一些简单的改动,打破堆的状态,然后再遍历堆并按照要求将堆的状态恢复。这个过程叫做堆的有序化(reheapifying)
可能遇到的两种情况:
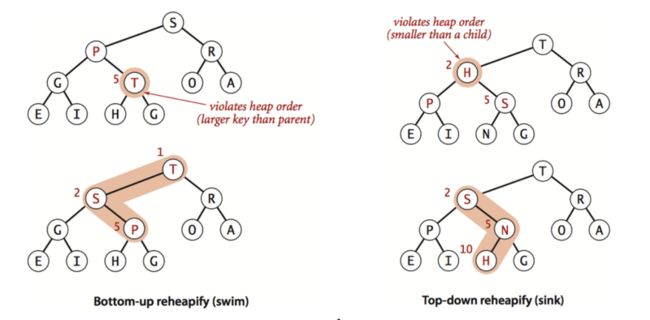
由下至上的堆有序化(上浮)
如果堆的有序状态因为某个节点变得比它的父节点更大而被打破,那么需要通过交换它和父节点位置来修复堆。交换后,这个节点比它的两个子节点都大,但是仍然可能比它现在的父节点大,可以一遍遍的用同样的方法恢复秩序,这个节点不断上移知道遇到一个更大的父节点。只要记住位置K的节点的父节点的位置是K/2,该过程实现简单。
由上至下的堆有序化(下沉)
如果有序状态因为某个节点变得比两个子节点或是其中之一更小而被打破,那么可以通过将它和两个子节点中的较大者交换来恢复有序状态。交换可能会在子节点出继续打破有序状态,因此需要不断用相同方法来修复,将节点向下移动知道它的子节点都比它更小或者到达了对的地步。由位置K的节点的子节点位于2K和2K+1处,可以实现代码。
例子:可以想象堆是一个严密的黑社会组织,每个子节点都表示一个下属,父节点表示它的直接上级。swim表示一个很有能力的新人加入组织并被逐级提升(将能力不够的上级踩在脚下),直到遇到一个更强的领导。sink则类似于整个社团的领导退休并被外来者取代后,如果他的下属比他更厉害,他们的角色就会交换,这种交换会持续下去直到他的能力比其他下属都强为止。
插入元素:新元素加到数组末尾;增加堆的大小;新元素上浮到合适的位置。
删除最大元素:从数组顶端删去最大的元素;并将数组的最后一个元素放到顶端;减小堆的大小;并让该元素下沉到合适的位置。
该算法对API的实现能够保证插入元素和删除最大元素这两个操作的用时和队列大小仅呈对数关系。
命题:对于一个含有N个元素的基于堆的优先级队列,插入元素操作只需要不超过lgN+1次比较,删除最大元素的操作需要不超过2lgN次比较。两种操作都需要在根节点和堆底之间移动元素,而路径的长度不超过lgN。对于路径上的每个节点,删除最大元素需要比较两次(除了堆底元素),一次用来找出较大的子节点,一次用来确定该子节点是否需要上浮。
多叉堆
构建完全三叉树结构
调整数组大小添加无参构造函数,在insert中添加将数组加倍的代码,在delMax中添加将数组长度减半的代码。
元素的不可变性优先级队列存储了用例创建的对象,但同时假设用例代码不会改变它们。可将这个假设转化为强制条件,但增加代码的复杂性会降低性能。
索引优先级队列
很多应用中,允许用例引用已进入优先级队列中的元素很有必要。
做到这一点的一种简单方法是给每个元素一个索引。
另外,一种常见的情况是用例已经有了总量为N的多个元素,而且可能还同时使用了多个平行数组来存储这些元素的信息。此时其他无关的用例代码可能已经在使用一个整数索引来引用这些元素了。
这些考虑引导我们设计了下列API。
将它看成一个能够快速访问其中最小元素的数组。
事实上还更好:能够快速访问数组的一个特定子集中的最小元素(指所有被插入的元素)。
换句话说:
可将名为pq的IndexMinPQ类优先级队列看做数组pq[0...n-1]中的一部分元素的代表。
将pq.insert(k,item)看做将k加入这个子集并使得pq[k]=item,
pq.change(k, item)则代表令pq[k]=item。
这两种操作没有改变其他操作所依赖的数据结构,其中最重要的就是delMin()(删除最小元素并返回它的索引)和change()(改变数据结构中的某个元素的索引—即pq[i]=item)。这些操作在许多应用中都很重要并且依赖于对元素的引用(索引)
命题:在一个大小为N的索引优先级队列中,插入元素insert、改变优先级change、删除delete和删除最小元素remove the minimum 这些操作所需的比较次数和lgN成正比。
此处留坑,以后再看,这是库中的源码
/**
* 索引优先级队列IndexMinPQ
*/
public class IndexMinPQ> implements Iterable {
private int maxN; // maximum number of elements on PQ
private int n; // number of elements on PQ
private int[] pq; // binary heap using 1-based indexing
private int[] qp; // inverse of pq - qp[pq[i]] = pq[qp[i]] = i
private Key[] keys; // keys[i] = priority of i
public IndexMinPQ(int maxN) {
this.maxN = maxN;
n = 0;
keys = (Key[]) new Comparable[maxN + 1]; // make this of length maxN??
pq = new int[maxN + 1];
qp = new int[maxN + 1]; // make this of length maxN??
for (int i = 0; i <= maxN; i++)
qp[i] = -1;
}
public boolean isEmpty() {return n == 0;}
public boolean contains(int i) {return qp[i] != -1;}
public int size() { return n;}
public void insert(int i, Key key) {
if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException();
if (contains(i)) throw new IllegalArgumentException("index is already in the priority queue");
n++;
qp[i] = n;
pq[n] = i;
keys[i] = key;
swim(n);
}
public int minIndex() {
if (n == 0) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
public Key minKey() {
if (n == 0) throw new NoSuchElementException("Priority queue underflow");
return keys[pq[1]];
}
public int delMin() {
if (n == 0) throw new NoSuchElementException("Priority queue underflow");
int min = pq[1];
exch(1, n--);
sink(1);
assert min == pq[n+1];
qp[min] = -1; // delete
keys[min] = null; // to help with garbage collection
pq[n+1] = -1; // not needed
return min;
}
public Key keyOf(int i) {
if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
else return keys[i];
}
public void changeKey(int i, Key key) {
if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
keys[i] = key;
swim(qp[i]);
sink(qp[i]);
}
public void decreaseKey(int i, Key key) {
if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
if (keys[i].compareTo(key) <= 0)
throw new IllegalArgumentException("Calling decreaseKey() with given argument would not strictly decrease the key");
keys[i] = key;
swim(qp[i]);
}
public void increaseKey(int i, Key key) {
if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
if (keys[i].compareTo(key) >= 0)
throw new IllegalArgumentException("Calling increaseKey() with given argument would not strictly increase the key");
keys[i] = key;
sink(qp[i]);
}
public void delete(int i) {
if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException();
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
int index = qp[i];
exch(index, n--);
swim(index);
sink(index);
keys[i] = null;
qp[i] = -1;
}
private boolean greater(int i, int j) {return keys[pq[i]].compareTo(keys[pq[j]]) > 0;}
private void exch(int i, int j) {
int swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
qp[pq[i]] = i;
qp[pq[j]] = j;
}
private void swim(int k) {
while (k > 1 && greater(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}
private void sink(int k) {
while (2*k <= n) {
int j = 2*k;
if (j < n && greater(j, j+1)) j++;
if (!greater(k, j)) break;
exch(k, j);
k = j;
}
}
public Iterator iterator() { return new HeapIterator(); }
private class HeapIterator implements Iterator {
// create a new pq
private IndexMinPQ copy;
// add all elements to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
copy = new IndexMinPQ(pq.length - 1);
for (int i = 1; i <= n; i++)
copy.insert(pq[i], keys[pq[i]]);
}
public boolean hasNext() { return !copy.isEmpty(); }
public void remove() { throw new UnsupportedOperationException(); }
public Integer next() {
if (!hasNext()) throw new NoSuchElementException();
return copy.delMin();
}
}
public static void main(String[] args) {
// insert a bunch of strings
String[] strings = { "it", "was", "the", "best", "of", "times", "it", "was", "the", "worst" };
IndexMinPQ pq = new IndexMinPQ(strings.length);
for (int i = 0; i < strings.length; i++)
pq.insert(i, strings[i]);
// delete and print each key
while (!pq.isEmpty()) {
int i = pq.delMin();
StdOut.println(i + " " + strings[i]);
}
StdOut.println();
// reinsert the same strings
for (int i = 0; i < strings.length; i++)
pq.insert(i, strings[i]);
// print each key using the iterator
for (int i : pq)
StdOut.println(i + " " + strings[i]);
}
} 索引优先级队列用例:
多向归并问题:将多个有序的输入流归并成一个有序的输入流。
输入流可能来自多种一起的输出(按时间排序),
或者来自多个音乐或电影网站的信息列表(按名称或者艺术家名字排序),
或是商业交易(按账号或时间排序)。
如果有足够的空间,可以简单地读入一个数组并排序,但用了优先级队列无论输入有多长你都可以把它们全部读入并排序。
/**
* 使用优先队列的多项归并
*/
public class Multiway {
public static void merge(In[] streams){
int n = streams.length;
IndexMinPQ pq = new IndexMinPQ(n);
for(int i = 0;i 结果
A A B B B C D E F F G H I I J N P Q Q Z
结果有了上面的扩展知识,下面来看堆排序:
可以把任意优先级队列变成一种排序方法。将所有元素插入一个查找最小元素的优先级队列,然后重复调用删除最小元素的操作将它们按顺序删除。
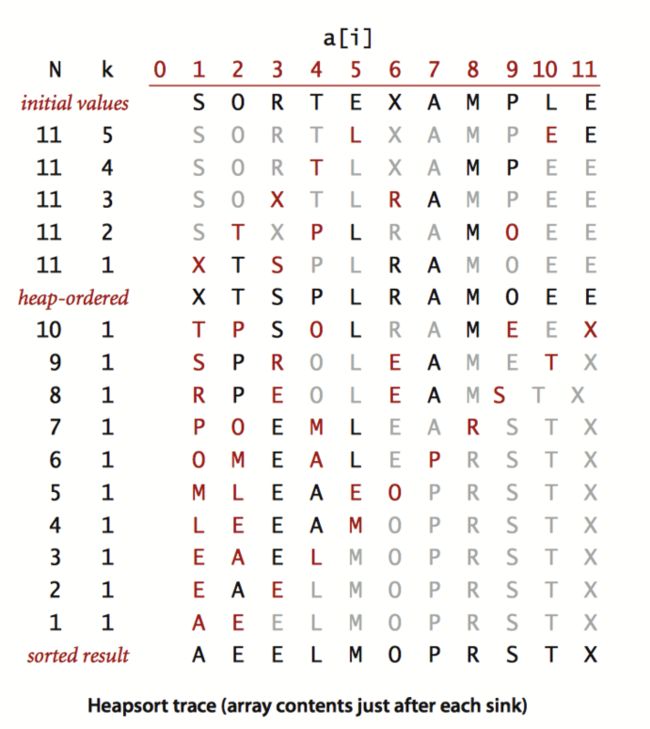
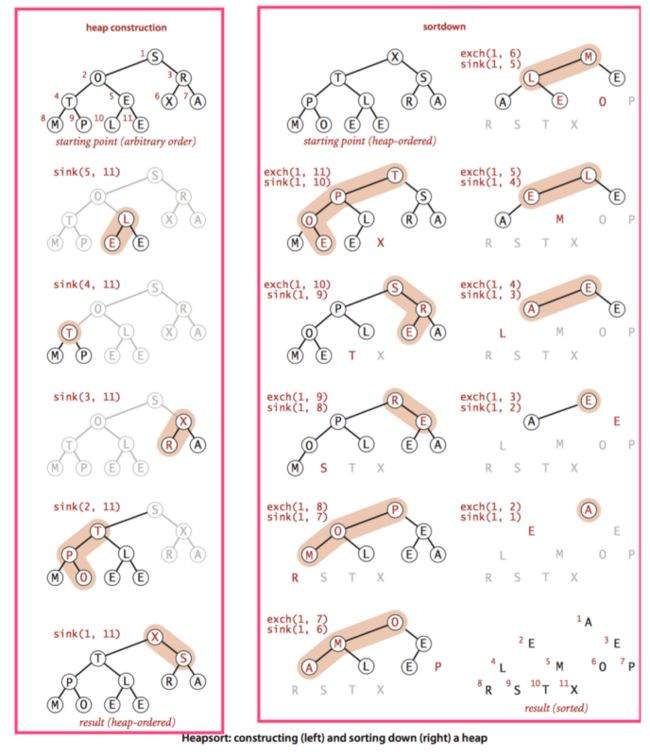
堆排序分为两个阶段。构造阶段中,将原始数组重新组织安排进一个堆中;然后在下沉排序阶段,从堆中按递减顺序取出所有元素并得到排序结果。
为了排序需要,不再将优先级队列的具体表示隐藏,将直接使用swim和sink操作。这样在排序时就可以将需要排序的数组本身作为堆,因此无需任何额外空间。
/**
* 堆排序
*/
public class HeapSort {
public static void sort(Comparable[] a){
int n = a.length - 1; // index=0的位置不使用, n是最后一个index
buildHeap(a, n);
while(n>1){
exchange(a,1,n--);
sink(a,1,n);
}
}
/**
* 构造堆
*/
private static void buildHeap(Comparable[] a, int n) {
for(int k = n/2; k>=1; k--)
sink(a, k, n);
}
private static void exchange(Comparable[] a, int i, int j) {
Comparable temp = a[i];
a[i] = a[j];
a[j] = temp;
}
private static void sink(Comparable[] a, int k, int n) {
while(2*k <= n){
int j = 2*k;
if(j结果:
[ , a, e, e, l, m, o, p, r, s, t, x]
该算法用sink方法将a[1]到a[n]的元素排序(n=len-1),sink接受的参数需要修改。
for循环构造堆,while循环将最大元素a[1]和a[n]交换并修复堆,如此重复直到堆变为空
调用exchange时索引减一即可
堆排序的主要工作是在第二阶段完成的。
删除堆中最大元素
放入堆缩小后数组空出的位置。
进行下沉操作。
命题R:用下沉操作由N个元素构造堆 只需要少于2N次比较以及少于N次交换。
命题S:将N个元素排序,堆排序只需要少于(2NlgN+2N)次比较(以及一半次数的交换)。
第一次for循环构造堆,第二次while循环在下沉排序中销毁堆。都是基于sink方法。
将该实现和优先级队列的API独立开是为了突出这个排序算法的简洁性,构造和sink分别只需几行代码。
堆排序在排序复杂性的研究中有很重要的地位,是所知的唯一能够同时最优的利用空间和时间的方法。
最坏情况也能保证2NlgN次比较和恒定的额外空间。空间紧张时很流行。
但是现代系统许多应用很少使用它,因为它无法利用缓存。数组元素很少和相邻元素进行比较,因此缓存Miss远远高于大多数比较都在相邻元素之间进行的算法。
上面的几种排序方法都是基于比较排序的算法。时间复杂度下界是O(nlogn)
下面介绍的三种排序是非基于比较的算法。计数排序,桶排序,基数排序。是可以突破O(nlogn)的下界的。
但是非基于比较的排序算法使用限制比较多。
计数排序进对较小整数进行排序,且要求排序的数据规模不能过大
基数排序可以对长整数进行排序,但是不适用于浮点数。
桶排序可以对浮点数进行排序
下面一一来学习。
7.计数排序
在排序的时候就知道其位置,那么就扫描一遍放入正确位置。如此以来,只需知道有多大范围就可以了。这就是计数排序的思想。
性能:时间复杂度O(n+k),线性时间,并且稳定!
优点:不需比较,利用地址偏移,对范围固定在[0,k]的整数排序的最佳选择。是排序字符串最快的排序算法
缺点:用来计数的数组的长度取决于带排序数组中数据的范围(等于待排序数组的最大值和最小值的差加1),这使得计数排序对于数据范围很大的数组,需要大量时间和空间。
/**
* 计数排序
*/
public class CountSort {
public static int[] sort(int[] array){
int[] result = new int[array.length]; // 存储结果
int max = max(array); // 找到待排序数组中的最大值max
int[] temp = new int[max+1]; // 申请一个大小为max+1的辅助数组
for(int i = 0; i=0; i--){
int v = array[i]; // 当前元素
result[temp[v] - 1] = v; // 当前元素作为索引,得到辅助数组元素,减一后的结果作为result中的索引,该处放置当前的遍历元素
temp[v] = temp[v] - 1; // 辅助数组相应位置减少1,以供下个相同元素索引到正确位置
}
return result;
}
private static int max(int[] array) {
int max = array[0];
for(int i = 1; i < array.length; i++)
if(array[i] > max) max = array[i];
return max;
}
public static void main(String[] args) {
int[] arr = {3,4,1,7,2,8,0};
int[] result = sort(arr);
System.out.println(Arrays.toString(result));
}
} http://zh.visualgo.net/sorting
如果手动比较难以理解,可参照以上链接的可视化过程来观察。
扩展:设计算法,对于给定的介于0--k之间的n个整数进行预处理,并在O(1)时间内得到这n个整数有多少落在了(a,b]区间内。以上算法即可用来处理,预处理的时间为O(n+k)。
用计数排序中的预处理方法,预处理辅助数组,使得temp[i]为不大于i的元素的个数。
(a,b]区间内元素个数即为temp[b] - temp[a]
/**
* 计数排序的扩展
*/
public class CountSortExt {
private int[] temp; // 辅助数组
public CountSortExt(int[] a){
int max = max(a);
temp = new int[max+1];
for(int i = 0; i结果为:
5
8.桶排序
参考http://www.growingwiththeweb....
使用场景:输入的待排序数组在一个范围内均匀分布。
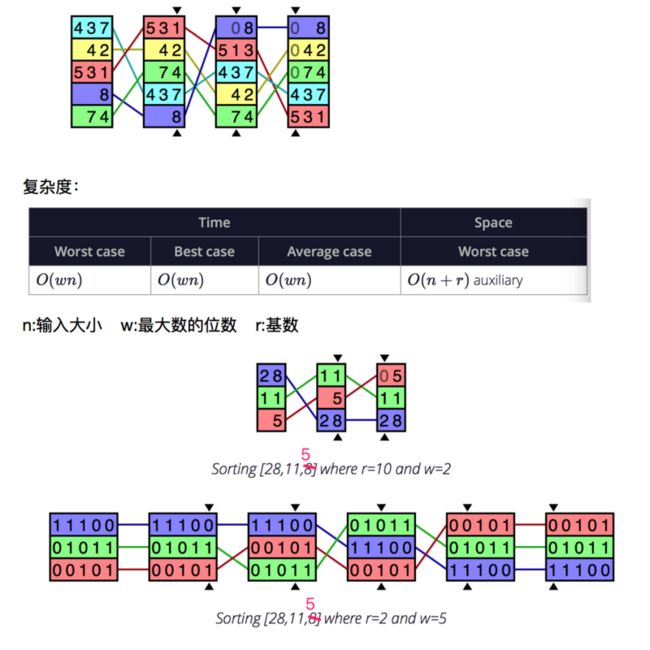
复杂度:
什么时候是最好情况呢?
O(n+k)的额外空间不是个事儿。
上面说到的使用场景:输入数组在一个范围内均匀分布。
那么什么时候是最坏呢?数组的所有元素都进入同一个桶。
/**
* 桶排序
*/
public class BucketSort {
private static final int DEFAULT_BUCKET_SIZE = 5;
public static void sort(Integer[] array){
sort(array, DEFAULT_BUCKET_SIZE);
}
public static void sort(Integer[] array, int size) {
if(array == null || array.length == 0) return;
// 找最大最小值
int min = array[0], max = array[0];
for(int i=1; i max) max = array[i];
}
// 初始化桶
int bucketCount = (max - min) / size + 1;
List> buckets = new ArrayList<>(bucketCount);
for(int i = 0; i < bucketCount; i++)
buckets.add(new ArrayList());
// 把输入数组均匀分布进buckets
for(int i = 0; i currentBucket = buckets.get(i);
Integer[] bucketArray = new Integer[currentBucket.size()];
bucketArray = currentBucket.toArray(bucketArray);
Arrays.sort(bucketArray);
for(int j = 0; j< bucketArray.length; j++)
array[currentIndex++] = bucketArray[j];
}
}
public static void main(String[] args) {
Integer[] array = {3,213,3,4,5,32,3,88,10};
sort(array);
System.out.println(Arrays.toString(array));
}
} [3, 3, 3, 4, 5, 10, 32, 88, 213]
9.基数排序
非比较型整数排序算法,原理是将整数按位切割成不同数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能适用于整数。
实现:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零,然后从最低位开始,依次进行一次排序,这样从最低位排序一直到最高位排序完成后,数列就变成有序的。
实现参考链接:
http://www.growingwiththeweb....
该基数排序基于LSD(Least significant digit),从最低有效关键字开始排序。首先对所有的数据按照次要关键字排序,然后对所有的数据按照首要关键字排序。
/**
* 基数排序
*/
public class RadixSort {
public static void sort(Integer[] array){
sort(array, 10);
}
private static void sort(Integer[] array, int radix) {
if(array == null || array.length == 0) return;
// 找最大最小值
int min = array[0], max = array[0];
for(int i = 1; i max) max = array[i];
}
int exponent = 1;
int off = max - min;
// 对每一位进行计数排序
while(off / exponent >= 1){
countingSortByDigit(array, radix, exponent, min);
exponent *= radix;
}
}
private static void countingSortByDigit(Integer[] array, int radix, int exponent, int min) {
int bucketIndex;
int[] buckets = new int[radix];
int[] output = new int[array.length];
// 初始化桶
for(int i=0; i=0; i--){
bucketIndex = (int)(((array[i] - min) / exponent) % radix);
output[--buckets[bucketIndex]] = array[i];
}
// 拷贝回去
for(int i =0; i 先总结到这里。