CS 188 (2) DepthFirstSearch DFS(深度优先搜索算法)
本文要实现DepthFirstSearch深度优先搜索算法,首先搜索搜索树中最深的节点,搜索算法返回到达目标。
传入的参数:搜索问题problem
要实现的深度优先算法位于search.py文件中,depthFirstSearch(problem)函数传入一个参数problem,problem是PositionSearchProblem位置搜索问题类的一个实例,PositionSearchProblem子类继承于SearchProblem父类。SearchProblem父类是一个抽象类,SearchProblem类概述了搜索问题的结构,但没有实现任何方法。PositionSearchProblem子类搜索问题继承父类重载定义了状态空间、开始状态、目标测试、后续任务、搜索成本函数,PositionSearchProblem搜索问题可用于查找路径在Pacman迷宫板上的一个特定点,状态空间由Pacman游戏中的(x,y)位置组成。
PositionSearchProblem类初始化时候存储开始和目标信息。
gameState是GameState对象 (pacman.py);
costFn:从搜索状态(元组)到非负数的函数;
目标goal:在gameState游戏状态中的位置;
属性_visited,_visitedlist用于展示用途。
getSuccessors函数返回后续状态、所需操作以及计量为1的成本。参考search.py中的getSuccessors注释:对于一个给定的状态,getSuccessors返回一个三元组列表(successor,action, stepCost)即:(后继,动作,步进成本),其中“后继”是当前的后继状态,“action”是到达目的地所需的操作,“stepcost”是扩展到那个继承者的增量成本。
getCostOfActions函数中的动作actions是要采取的动作列表,getCostOfActions方法返回特定操作序列的总成本。序列必须由合法的移动组成。如果这些行动包含非法的移动,则返回999999。(根据游戏墙self.walls[x][y]是否为1或者actions == None判断。)
查看搜索问题的初始状态:
开始深度优先算法编码前,您可能需试图打印以下一些简单命令,了解正在传入的搜索问题。
print("Start:", problem.getStartState())
print("Is the start a goal?", problem.isGoalState(problem.getStartState()))
print("Start's successors:", problem.getSuccessors(problem.getStartState()))显示如下,pac man的起始点是(5,5),后续的状态是一个三元组(下一个可能的节点坐标,动作方向,计量成本):
[SearchAgent] using function depthFirstSearch
[SearchAgent] using problem type PositionSearchProblem
Start: (5, 5)
Is the start a goal? False
Start's successors: [((5, 4), 'South', 1), ((4, 5), 'West', 1)]深度优先搜索算法DFS:
Stack是一个后进先出(LIFO)队列策略的容器,其实Stack是一个类,使用列表List初始化,入站和出站通过列表List的append和pop实现,从列表的长度为0判断栈是否为空。
class Stack:
"A container with a last-in-first-out (LIFO) queuing policy."
def __init__(self):
self.list = []
def push(self,item):
"Push 'item' onto the stack"
self.list.append(item)
def pop(self):
"Pop the most recently pushed item from the stack"
return self.list.pop()
def isEmpty(self):
"Returns true if the stack is empty"
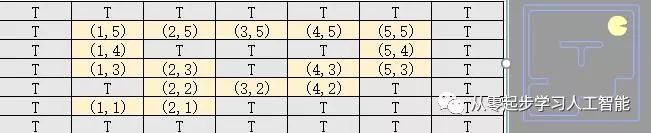
return len(self.list) == 0案例使用tinyMaze布局,布局的可视化暂忽略,从搜索问题problem的walls属性信息中可以获取迷宫墙的数字信息,如下图所示,要从(5,5)点到达(1,1)点:
在本文案例中,pac man移动北、南、东、西移动与x,y的坐标变换关系:
DFS代码如下:
# search.py
# ---------
# Licensing Information: You are free to use or extend these projects for
# educational purposes provided that (1) you do not distribute or publish
# solutions, (2) you retain this notice, and (3) you provide clear
# attribution to UC Berkeley, including a link to http://ai.berkeley.edu.
#
# Attribution Information: The Pacman AI projects were developed at UC Berkeley.
# The core projects and autograders were primarily created by John DeNero
# ([email protected]) and Dan Klein ([email protected]).
# Student side autograding was added by Brad Miller, Nick Hay, and
# Pieter Abbeel ([email protected]).
def depthFirstSearch(problem):
"""
Search the deepest nodes in the search tree first.
Your search algorithm needs to return a list of actions that reaches the
goal. Make sure to implement a graph search algorithm.
To get started, you might want to try some of these simple commands to
understand the search problem that is being passed in:
print("Start:", problem.getStartState())
print("Is the start a goal?", problem.isGoalState(problem.getStartState()))
print("Start's successors:", problem.getSuccessors(problem.getStartState()))
"""
"*** YOUR CODE HERE ***"
#util.raiseNotDefined()
print("Start:", problem.getStartState())
print("Is the start a goal?", problem.isGoalState(problem.getStartState()))
print("Start's successors:", problem.getSuccessors(problem.getStartState()))
path = Path([problem.getStartState()],[],0)
if problem.isGoalState(problem.getStartState()):
return path.directions
#新建一个堆栈,起始状态入栈
stack = util.Stack()
stack.push(path)
while not stack.isEmpty():
#如栈不为空,取栈顶的第一个元素,获取当前路径
currentPath = stack.pop()
currentLocation = currentPath.locations[-1]
#如果当前位置已经是终点的位置,则返回当前路径的方向列表,用于移动pac man。
if problem.isGoalState(currentLocation):
return currentPath.directions
else:
#在搜索问题中取得当前位置后继的下一个状态.getSuccessors中for循环遍历北、南、东、西四个方向,
#directionToVector取得方向到坐标偏移向量的转换值,在当前坐标上加上位移的坐标偏移量值,
#如果下一步坐标移动的点不是围墙,则在后续状态列表中加入三元组( nextState, action, cost)
nextSteps= problem.getSuccessors(currentLocation)
for nextStep in nextSteps:
#遍历下一步的状态,依次获得位置、方向、成本信息
nextLocation =nextStep[0]
nextDirection =nextStep[1]
nextCost =nextStep[2]
# 为了不走环路,判断位置不在已经走过的路径里面.已经走过的位置,不再遍历。
if nextLocation not in currentPath.locations:
#获取当前路径列表集
nextLocations =currentPath.locations[:]
#将新的位置加入到当前路径的列表里面
nextLocations.append(nextLocation)
print("当前位置:",currentLocation)
print("当前位置下一步可能的移动位置:",nextLocation)
print("加到当前位置列表集:",nextLocations)
print()
print()
#print(currentLocation,nextLocation,nextLocations)
#获取当前的方向集
nextDirections = currentPath.directions[:]
#将新的方向加入到当前方向集的列表里面
nextDirections.append(nextDirection)
nextCosts = currentPath.cost +nextCost
nextPath =Path(nextLocations,nextDirections,nextCosts)
#下一步的状态,入栈
stack.push(nextPath)
#栈为空,仍未到达终点,返回空集
return []
DFS深度优先搜索算法的遍历结果:
其中的locations列出了每一步走的位置,directions列出了每一步的方向。
[SearchAgent] using function depthFirstSearch
[SearchAgent] using problem type PositionSearchProblem
Start: (5, 5)
Is the start a goal? False
Start's successors: [((5, 4), 'South', 1), ((4, 5), 'West', 1)]
当前位置: (5, 5)
当前位置下一步可能的移动位置: (5, 4)
加到当前位置列表集: [(5, 5), (5, 4)]
当前位置: (5, 5)
当前位置下一步可能的移动位置: (4, 5)
加到当前位置列表集: [(5, 5), (4, 5)]
当前位置: (4, 5)
当前位置下一步可能的移动位置: (3, 5)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5)]
当前位置: (3, 5)
当前位置下一步可能的移动位置: (2, 5)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5)]
当前位置: (2, 5)
当前位置下一步可能的移动位置: (1, 5)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5)]
当前位置: (1, 5)
当前位置下一步可能的移动位置: (1, 4)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4)]
当前位置: (1, 4)
当前位置下一步可能的移动位置: (1, 3)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3)]
当前位置: (1, 3)
当前位置下一步可能的移动位置: (2, 3)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3)]
当前位置: (2, 3)
当前位置下一步可能的移动位置: (2, 2)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2)]
当前位置: (2, 2)
当前位置下一步可能的移动位置: (2, 1)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2), (2, 1)]
当前位置: (2, 2)
当前位置下一步可能的移动位置: (3, 2)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2), (3, 2)]
当前位置: (3, 2)
当前位置下一步可能的移动位置: (4, 2)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2), (3, 2), (4, 2)]
当前位置: (4, 2)
当前位置下一步可能的移动位置: (4, 3)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2), (3, 2), (4, 2), (4, 3)]
当前位置: (4, 3)
当前位置下一步可能的移动位置: (5, 3)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2), (3, 2), (4, 2), (4, 3), (5, 3)]
当前位置: (5, 3)
当前位置下一步可能的移动位置: (5, 4)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2), (3, 2), (4, 2), (4, 3), (5, 3), (5, 4)]
当前位置: (2, 1)
当前位置下一步可能的移动位置: (1, 1)
加到当前位置列表集: [(5, 5), (4, 5), (3, 5), (2, 5), (1, 5), (1, 4), (1, 3), (2, 3), (2, 2), (2, 1), (1, 1)]
Path found with total cost of 10 in 0.0 seconds
Search nodes expanded: 16
Pacman emerges victorious! Score: 500
Average Score: 500.0
Scores: 500.0
Win Rate: 1/1 (1.00)
Record: Win
欢迎关注微信公众号:“从零起步学习人工智能”。