cvxpy学习笔记
CVXPY的作用
与matlab中cvx的工具包类似,用于求解凸优化问题。cvx与cvxpy都是由CIT的Stephen Boyd教授课题组开发。cvx用于matlab的包,cvxpy是用于python的包。下载、安装及学习地址如下:
[CVX](http://cvxr.com/cvx/)
[CVXPY](http://www.cvxpy.org/)
一、CVXPY入门
## 简单例子 ##
import cvxpy as cvx
#定义优化变量
x = cvx.Variable()
y = cvx.Variable()
# 定义约束条件
constraints = [x + y == 1,
x - y >= 1]
# 定义优化问题
obj = cvx.Minimize((x - y)**2)
# 定义优化问题
prob = cvx.Problem(obj, constraints)
#求解问题
prob.solve() #返回最优值
print("status:", prob.status) #求解状态
print("optimal value", prob.value) #目标函数优化值
print("optimal var", x.value, y.value) #优化变量的值,相应变量加.value
#运行结果
status: optimal
optimal value 0.999999999761 #最优值视为 1(计算机精度问题)
optimal var 1.00000000001 -1.19961841702e-11 (x=1,y=0)
# 改变目标函数,利用已定义问题的约束,**问题被定义后,不可改变
prob2 = cvx.Problem(cvx.Maximize(x + y), prob.constraints)
print("optimal value", prob2.solve())
# 改变约束
constraints = [x + y <= 3] + prob.constraints[1:]
prob2 = cvx.Problem(prob.objective, constraints)
print("optimal value", prob2.solve())
#运行结果
optimal value 1.0
optimal value 3.00000000006
二、求解状态(XXX.status)
| 求解状态 | 含义 |
|---|---|
| OPTIMAL | 最优解 |
| INFEASIBLE | 不可行 |
| UNBOUNDED | 无界 |
| OPTIMAL_INACCURATE | 不精确 |
| INFEASIBLE_INACCURATE | 不精确 |
| UNBOUNDED_INACCURATE | 不精确 |
对于opyimal情况,求解的就是最优解,对于infeasible与unbounded见2.1节。对于后三种情况,表明求解精度低(低于期望精度),如果求解器抛出异常(SolverError),可以尝试选择其他求解器。见2.2节。
2.1 不可行及无界情况
import cvxpy as cvx
x = cvx.Variable()
# 不可行问题
prob = cvx.Problem(cvx.Minimize(x), [x >= 1, x <= 0])
prob.solve()
print("status:", prob.status)
print("optimal value", prob.value)
# 无界问题
prob = cvx.Problem(cvx.Minimize(x))
prob.solve()
print("status:", prob.status)
print("optimal value", prob.value)
#运行结果
status: infeasible
optimal value inf
status: unbounded
optimal value -inf
对minimization问题,infeasible对应inf,unbounded对应-inf;maximization问题反之。
###2.2 求解器选择
各求解器能求解的问题:
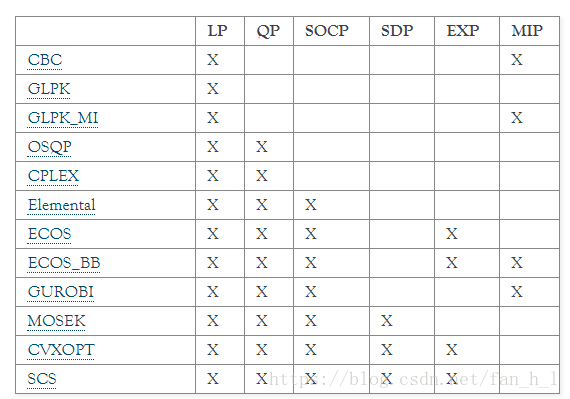
# Solving a problem with different solvers.
x = cvx.Variable(2)
obj = cvx.Minimize(x[0] + cvx.norm(x, 1))
constraints = [x >= 2]
prob = cvx.Problem(obj, constraints)
# Solve with ECOS.
prob.solve(solver=cvx.ECOS)
print("optimal value with ECOS:", prob.value)
# Solve with ECOS_BB.
prob.solve(solver=cvx.ECOS_BB)
print("optimal value with ECOS_BB:", prob.value)
# Solve with CVXOPT.
prob.solve(solver=cvx.CVXOPT)
print("optimal value with CVXOPT:", prob.value)
# Solve with SCS.
prob.solve(solver=cvx.SCS)
print("optimal value with SCS:", prob.value)
# Solve with GLPK.
prob.solve(solver=cvx.GLPK)
print("optimal value with GLPK:", prob.value)
# Solve with GLPK_MI.
prob.solve(solver=cvx.GLPK_MI)
print("optimal value with GLPK_MI:", prob.value)
# Solve with GUROBI.
prob.solve(solver=cvx.GUROBI)
print("optimal value with GUROBI:", prob.value)
# Solve with MOSEK.
prob.solve(solver=cvx.MOSEK)
print("optimal value with MOSEK:", prob.value)
# Solve with Elemental.
prob.solve(solver=cvx.ELEMENTAL)
print("optimal value with Elemental:", prob.value)
# Solve with CBC.
prob.solve(solver=cvx.CBC)
print("optimal value with CBC:", prob.value)
optimal value with ECOS: 5.99999999551
optimal value with ECOS_BB: 5.99999999551
optimal value with CVXOPT: 6.00000000512
optimal value with SCS: 6.00046055789
optimal value with GLPK: 6.0
optimal value with GLPK_MI: 6.0
optimal value with GUROBI: 6.0
optimal value with MOSEK: 6.0
optimal value with Elemental: 6.0000044085242727
optimal value with CBC: 6.0
//Use the installed_solvers utility function to get a list of the solvers your installation of CVXPY //supports.
print installed_solvers()
['CBC', 'CVXOPT', 'MOSEK', 'GLPK', 'GLPK_MI', 'ECOS_BB', 'ECOS', 'SCS'
变量类型 (Variable)##
变量可以是标量、向量以及矩阵
# 标量
a = cvx.Variable()
# 向量
x = cvx.Variable(5)
# 矩阵大小为(5, 1).
x = cvx.Variable((5, 1))
# 矩阵大小为(4, 7).
A = cvx.Variable((4, 7))
cvxpy中可以做常数使用的用:
- NumPy ndarrays
- NumPy matrices
- SciPy sparse matrices
# Solves a bounded least-squares problem.
import cvxpy as cvx
import numpy
# Problem data.
m = 10
n = 5
numpy.random.seed(1)
A = numpy.random.randn(m, n)
b = numpy.random.randn(m)
# Construct the problem.
x = cvx.Variable(n)
objective = cvx.Minimize(cvx.sum_squares(A*x - b))
constraints = [0 <= x, x <= 1]
prob = cvx.Problem(objective, constraints)
print("Optimal value", prob.solve())
print("Optimal var")
print(x.value) # A numpy ndarray.**
#运行结果
Optimal value 4.14133859146
Optimal var
[ -5.11480673e-21 6.30625742e-21 1.34643668e-01 1.24976681e-01
-4.79039542e-21]
三、约束(constraint)
可以使用 ==, <=,>= ,不能使用< ,>(没有意义,不接收)。也不能使用0 <= x <= 1(与cvx不同) or x == y == 2.(不能识别)
约束:[0 <= x , x <= 1],意味着x的每个元素都在0,1之间。
四、参数(parameters)
parameters可以理解为参数求解问题里的一个常数,可以是标量、向量、矩阵。在没有求解问题前(xxx.solve()),其允许你改变其值。【有点难理解,看一下下面的例子。】
#paraters的定义与赋值
# Positive scalar parameter.
m = cvx.Parameter(nonneg=True)
# Column vector parameter with unknown sign (by default).
c = cvx.Parameter(5)
# Matrix parameter with negative entries.
G = cvx.Parameter((4, 7), nonpos=True)
# Assigns a constant value to G.
G.value = -numpy.ones((4, 7))
# Create parameter, then assign value.
rho = cvx.Parameter(nonneg=True)
rho.value = 2
# Initialize parameter with a value.
rho = cvx.Parameter(nonneg=True, value=2)
#使用实例
import cvxpy as cvx
import numpy
import matplotlib.pyplot as plt
# Problem data.
n = 15
m = 10
numpy.random.seed(1)
A = numpy.random.randn(n, m)
b = numpy.random.randn(n)
# gamma must be nonnegative due to DCP rules.
gamma = cvx.Parameter(nonneg=True)
# Construct the problem.
x = cvx.Variable(m)
error = cvx.sum_squares(A*x - b)
obj = cvx.Minimize(error + gamma*cvx.norm(x, 1))
prob = cvx.Problem(obj)
# Construct a trade-off curve of ||Ax-b||^2 vs. ||x||_1
sq_penalty = []
l1_penalty = []
x_values = []
gamma_vals = numpy.logspace(-4, 6)
for val in gamma_vals:
gamma.value = val
prob.solve()
# Use expr.value to get the numerical value of
# an expression in the problem.
sq_penalty.append(error.value)
l1_penalty.append(cvx.norm(x, 1).value)
x_values.append(x.value)
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.figure(figsize=(6,10))
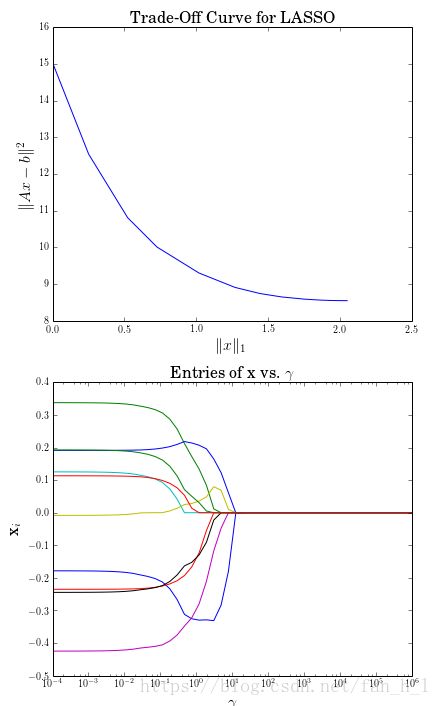
# Plot trade-off curve.
plt.subplot(211)
plt.plot(l1_penalty, sq_penalty)
plt.xlabel(r'\|x\|_1', fontsize=16)
plt.ylabel(r'\|Ax-b\|^2', fontsize=16)
plt.title('Trade-Off Curve for LASSO', fontsize=16)
# Plot entries of x vs. gamma.
plt.subplot(212)
for i in range(m):
plt.plot(gamma_vals, [xi[i] for xi in x_values])
plt.xlabel(r'\gamma', fontsize=16)
plt.ylabel(r'x_{i}', fontsize=16)
plt.xscale('log')
plt.title(r'\text{Entries of x vs. }\gamma', fontsize=16)
plt.tight_layout()
plt.show()
from multiprocessing import Pool
# Assign a value to gamma and find the optimal x.
def get_x(gamma_value):
gamma.value = gamma_value
result = prob.solve()
return x.value
# Parallel computation (set to 1 process here).
pool = Pool(processes = 1)
x_values = pool.map(get_x, gamma_vals)
如需转载或参考,请注明引用地址。