深度学习1-- 感知器
单层感知机
计算部分
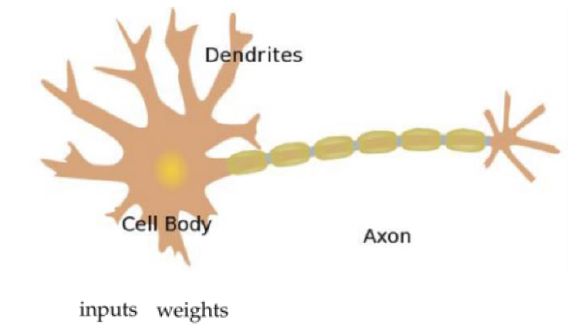
简述: 由人类神经元结构衍生而来,包含输入层和输出层,而输入层和输出层是直接相连的。
神经元结构
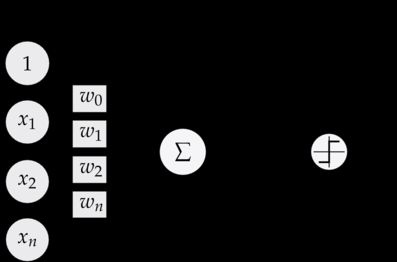
输出层结构如下:
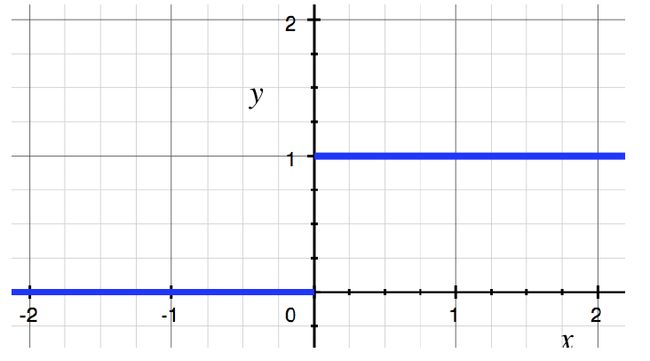
y = f ( ∑ i w i x i + b ) f ( x ) = { 1 , x ≥ 0 0 , x < 0 y = f( \sum_i w_ix_i + b) \\ f(x) = \begin{cases} 1, & \text{$x \geq 0$} \\[2ex] 0, & \text{$x < 0$} \end{cases} y=f(i∑wixi+b)f(x)=⎩⎨⎧1,0,x≥0x<0
结构如下图:
这里我们把偏置 b 归纳到 w 0 , x 0 w_0,x_0 w0,x0 中 令 x 0 x_0 x0 = 1, w 0 = 0 w_0 = 0 w0=0
从而简化上面的等式为:
y = f ( ∑ i w i x i ) y = f( \sum_i w_ix_i) y=f(i∑wixi)
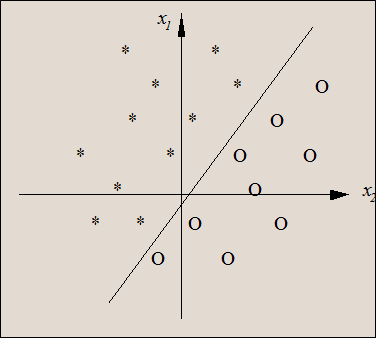
从几何意义上理解,决策面把下面两类分开。把上面的判断为1,下面的判断为0 。可能的解把下面的蓝点 和上面的红点正确分割的所有的线。线性分割后与权重向量方向相同的输出为1 ,相反的输出为0 。 多维空间可理解为一个超平面,超平面上的点输入也为0.
权重迭代部分
与最早提出的MP模型不同,神经元突触权值可变,因此可以通过一定规则进行学习。可以快速、可靠地解决线性可分的问题。
权重调整迭代公式如下:
w n e w = w o l d + η ( t − y ) w b n e w = b o l d + η ( t − y ) w_{new} = w_{old} + \eta(t-y)w \\ b_{new} = b_{old} + \eta(t-y) wnew=wold+η(t−y)wbnew=bold+η(t−y)
g r a d w grad_w gradw 是损失函数对于权重的梯度,损失函数定义为 L ( w , b ) = − ( t − y ) ( x ⋅ w + b ) L(w,b) = -(t-y)(x \cdot w +b) L(w,b)=−(t−y)(x⋅w+b) 。
其中 t 为 ground Truth,y 为我们预测的结果
对应的 w 和 b 的 梯度为:
g r a d w = ∂ L ∂ w = − ( t − y ) x grad_{w} = \frac{\partial L}{\partial w} = -(t -y) x gradw=∂w∂L=−(t−y)x , 实际中我们常用: g r a d w = ∂ L ∂ w = − 1 m ( t − y ) x grad_{w} = \frac{\partial L}{\partial w} = - \frac{1}{m}(t -y) x gradw=∂w∂L=−m1(t−y)x
g r a d b = ∂ L ∂ b = − ( t − y ) grad_{b} = \frac{\partial L}{\partial b} = -(t -y) gradb=∂b∂L=−(t−y) ,实际中我们常用: g r a d b = ∂ L ∂ b = − 1 m ( t − y ) grad_{b} = \frac{\partial L}{\partial b} = - \frac{1}{m}(t -y) gradb=∂b∂L=−m1(t−y)
实现一些逻辑运算
通过感知器我们能够实现不同的逻辑运算
例如 逻辑的与、或、非
| 实现操作 | 权重矩阵 |
|---|---|
| 与 | [-3,2,2] |
| 或 | [-1,2,2] |
| 非 | [1,-2] |
| 与非 | [3,-2,-2] |
x 向量传入 [1 ,0] [0,1] [1,1] [0,0] 可以得到需要的结果
感知器的缺陷
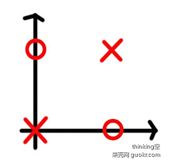
不能实现异或等逻辑操作。因为异或问题在二维平面上的分布如上图所示,是一个线性不可分的问题。 如下图所示,不能通过一条直线进行完全分离
代码实现
import numpy as np
samples_and = [
[0, 0, 0],
[1, 0, 0],
[0, 1, 0],
[1, 1, 1],
]
samples_or = [
[0, 0, 0],
[1, 0, 1],
[0, 1, 1],
[1, 1, 1],
]
samples_xor = [
[0, 0, 0],
[1, 0, 1],
[0, 1, 1],
[1, 1, 0],
]
def perceptron(samples):
w = np.array([1, 2])
b = 0
a = 1
for i in range(10):
for j in range(4):
x = np.array(samples[j][:2])
y = 1 if np.dot(w, x) + b > 0 else 0
d = np.array(samples[j][2])
delta_b = a*(d-y)
delta_w = a*(d-y)*x
print('epoch {} sample {} [{} {} {} {} {} {} {}]'.format(
i, j, w[0], w[1], b, y, delta_w[0], delta_w[1], delta_b
))
w = w + delta_w
b = b + delta_b
if __name__ == '__main__':
print('logical and')
perceptron(samples_and)
print('logical or')
perceptron(samples_or)
print('logical xor')
perceptron(samples_xor)