java 集合类之HashMap
本文从源代码角度简单介绍HashMap。
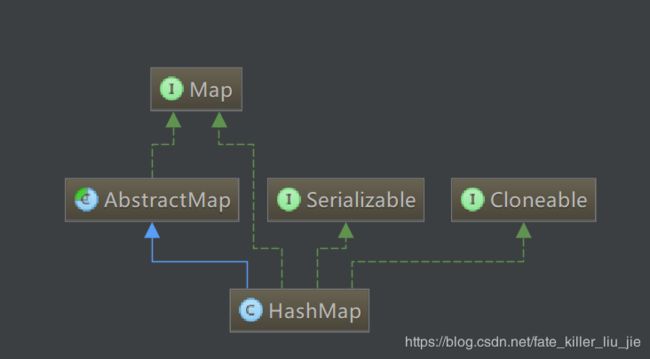
继承架构
可以看出,HashMap主要是继承了AbstractMap,实现了Map接口。类似的继承了AbstractMap的还有ConcurrentHashMap,TreeMap等等
抽象数据模型
HashMap的抽象数据模型来自于算法中查找技术的散列算法针对碰撞提出的拉链表。具体示意图如下:拉链表

散列表是为了快速查找而设计的一类数据结构,为了能快速定位到元素的位置,在存储元素的时候使用散列算法计算出键和存储位置的对应关系,这样在查找元素的时候只需要按照键计算出存储位置即可找到元素,不用遍历查找。但是不同的键可能会计算出相同的存储位置,也就是发生了碰撞,此时就要解决碰撞,一种简单的方法是发生碰撞之后查找碰撞点之后的存储空间是否空余,依次往后存储,这种方法相对简单,但是也会加大碰撞的概率。另一种方法则是使用链表存储hash相同的元素,就如同上面的示例一样。
重要字段
1 默认初始容量 16
/**
* The default initial capacity - MUST be a power of two.
*/
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
2 最大容量 2^30
/**
* The maximum capacity, used if a higher value is implicitly specified
* by either of the constructors with arguments.
* MUST be a power of two <= 1<<30.
*/
static final int MAXIMUM_CAPACITY = 1 << 30;
3 load factor
/**
* The load factor used when none specified in constructor.
*/
static final float DEFAULT_LOAD_FACTOR = 0.75f;
load factor 指的是resize的容量限制,load factor的选择关系到HashMap的性能,如果太大,则碰撞会增多,查询的开销会更大。如果太小,resize太频繁且空间利用率太低。使用0.75作为一个默认值是一个较为折衷的方案。
else {
// zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
以上的代码片段摘自resize()函数,可以看到,在没有指定初始容量的大多数情况下,初始的threshold等于 (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);而随着resize的进行,threshold每次乘2,和capacity以相同的速度增长。一直都是(int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);这么大。
4 转为红黑树的阈值
/**
* The bin count threshold for using a tree rather than list for a
* bin. Bins are converted to trees when adding an element to a
* bin with at least this many nodes. The value must be greater
* than 2 and should be at least 8 to mesh with assumptions in
* tree removal about conversion back to plain bins upon
* shrinkage.
*/
static final int TREEIFY_THRESHOLD = 8;
这个jdk 8新增的优化,在1.7的时候,为了优化查找,会使用尾插法来使得查找最近插入的记录变得更容易,1.8则使用红黑树来使链表很长时查找更快速。在理想情况下,即key完全随机分布,HashMap每个桶上面的元素(即hash相同的key)的个数服从泊松分布,依次计算出长度为0到8的概率如下:
* 0: 0.60653066
* 1: 0.30326533
* 2: 0.07581633
* 3: 0.01263606
* 4: 0.00157952
* 5: 0.00015795
* 6: 0.00001316
* 7: 0.00000094
* 8: 0.00000006
* more: less than 1 in ten million
说明长度大于8的链出现的概率很小,因此选用了8作为阈值
5 table数组
/**
* The table, initialized on first use, and resized as
* necessary. When allocated, length is always a power of two.
* (We also tolerate length zero in some operations to allow
* bootstrapping mechanics that are currently not needed.)
*/
transient Node<K,V>[] table;
这个field就是保存数据的散列表。解释一下为什么这个Field是transient的,transient是使本field不参与序列化,如果注意到了,就会发现ArrayList的elements数组,LinkedList的头指针和尾指针也都是transient的,这是为什么呢?如果是这样的话岂不是都没法序列化到真正的数据了吗,其实不然,序列化的关键在于readObject()和writeObject(),实现了这两个方法的类在反序列化/序列化的时候是直接调用这两个方法而不是序列化域。解决了能否序列化的问题,那么为什么不直接序列化数组呢,原因是key和bucketIndex的对应关系取决于hashCode()函数的实现,这个函数是一个native方法,在不同的平台实现不同,举例说明,加入key "abc"在windows平台下hashCode()返回1 在linux平台下返回2,那么将key为abc的某个值放到第1个bucket之后发送到linux平台中反序列化,那么按照key计算出来的bucketIndex是2,将会取不到正确的值。
6 entrySet
/**
* Holds cached entrySet(). Note that AbstractMap fields are used
* for keySet() and values().
*/
transient Set<Map.Entry<K,V>> entrySet;
这个是一个接口,提供给entrySet()抽象方法使用,但是需要注意的是,这个看起来像个集合类实例的field里面并没有保存任何数据,其foreach和iterator方法都是对table的遍历,而这一切的基础都是Node是Map.Entry的实现类。除此之外,keySet(),values()这些方法也都是这样实现的。
public Set<Map.Entry<K,V>> entrySet() {
Set<Map.Entry<K,V>> es;
return (es = entrySet) == null ? (entrySet = new EntrySet()) : es;
}
final class EntrySet extends AbstractSet<Map.Entry<K,V>> {
// 只是返回了外部类的size,实际上都是对table field进行的操作
public final int size() { return size; }
public final void clear() { HashMap.this.clear(); }
public final Iterator<Map.Entry<K,V>> iterator() {
return new EntryIterator();
}
public final boolean contains(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>) o;
Object key = e.getKey();
Node<K,V> candidate = getNode(hash(key), key);
return candidate != null && candidate.equals(e);
}
public final boolean remove(Object o) {
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>) o;
Object key = e.getKey();
Object value = e.getValue();
return removeNode(hash(key), key, value, true, true) != null;
}
return false;
}
public final Spliterator<Map.Entry<K,V>> spliterator() {
return new EntrySpliterator<>(HashMap.this, 0, -1, 0, 0);
}
public final void forEach(Consumer<? super Map.Entry<K,V>> action) {
Node<K,V>[] tab;
if (action == null)
throw new NullPointerException();
if (size > 0 && (tab = table) != null) {
int mc = modCount;
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next)
action.accept(e);
}
if (modCount != mc)
throw new ConcurrentModificationException();
}
}
}
核心方法实现
1 put()
put(K,V)可以将一个键值对隐射放入table中
// 暴露出去的put方法,供用户调用
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
// 定义临时变量处理,避免直接使用field继续操作
Node<K,V>[] tab; Node<K,V> p; int n, i;
// 假如尚未初始化,则开始初始化,注意调用默认构造函数没有初始化,所以这个分支是经常运行的
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// 假如该bucket没有值,也就是没有碰撞,那么直接放入该bucket
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
// 假如发生了碰撞,记录下现有的值
Node<K,V> e; K k;
// 判断是只有hash相同还是key也相同
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// key相同,是更新操作
e = p;
else if (p instanceof TreeNode)
// 仅仅是hash相同,是新增操作,而且当前的bucket链已经转化为红黑树,生成一个新的结点
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// 是新增,而且不是红黑树
for (int binCount = 0; ; ++binCount) {
// 遍历直到当前bucket 链表的末尾
if ((e = p.next) == null) {
// 尾插法插入数据
p.next = newNode(hash, key, value, null);
// 如果加上当前这个长度>= TREEIFY_THRESHOLD,那么久转为红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st,这里是补上当前的这个
treeifyBin(tab, hash);
break;
}
// 如果在链表里面找到了key相同的元素,那么记录这个元素
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 前面将key已存在的所有情况里,原来的元素都赋值给了e
// 这里判断是否是只新增,不更新,然后决定是否更新
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
// 如果容量超过了限制,就扩容
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
2 resize()
扩容方法,在大小超过限制时扩容
/**
* Initializes or doubles table size. If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
* 初始化或者将容量加倍。假如是空的,使用初始容量来建立存储空间。否则,因为我们使用加倍的
* 方法来扩容,那么在扩容之后的新table里,每个bin里面的元素要么还留在原来的位置,要么移动到
* 2的幂次
* @return the table
*/
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
// 如果还没初始化,oldCap为0 ,否则为旧表的长度
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
// 如果是扩容操作,不是初始化操作
if (oldCap > 0) {
// 如果已经到了容量限制,那么不再扩容,只是扩大threshold,使得不再出发扩容
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 如果没到容量限制,而且旧表的大小大于默认大小,那么将容量和threshold加倍
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
// 如果没有初始化,但是设置了初始容量,就将容量设置为threshold,这个threshold是通过
// tableSizeFor()的函数算来的,这个函数可以计算出比当前数大的最小2的n次幂
// 如tablseSizeFor(10)=16,tableSizeFor(3)=4
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
// 假如是使用了无参构造函数之后的初始化,那么直接设置容量为初始容量
// 设置threshold为load factor* capacity
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// 如果是设置了初始容量之后的初始化,那么设置一下threshold
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
// 创建新的散列表
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
// 如果不是初始化,是扩容那么执行复制
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
// 如果这个bucket不是空
if ((e = oldTab[j]) != null) {
// 设置旧的为空,避免内存泄漏
oldTab[j] = null;
// 如果没有链就直接复制过去
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// 如果是个红黑树节点,那么划分为low树和high树
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
// 划分链表
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
// 注意这个地方的e.hash & oldCap只能是0或oldCap,因为oldCap是2的整数次幂,
// 也就是2进制只有一个1,这样可以随机将链表分为两个部分
if ((e.hash & oldCap) == 0) {
// 将所有(e.hash & oldCap) == 0的放到低表里
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
// 将所有(e.hash & oldCap) == oldCap的放到高表里
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// 低表的数据不变
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
// 高表的数据往后移oldCap个单位
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
/**
* 划分红黑树的算法
*/
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;
// Relink into lo and hi lists, preserving order
// 和划分链的算法类似,一个高树一个低树
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
// 将hash & capacity ==0 的放入loHead的链表中
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
// 将hash & capacity !=0 的放入hiTail的链表中
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
// 根据长度判断是继续保留树结构还是不再保留树结构
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD)
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
if (hiHead != null) // (else is already treeified)
loHead.treeify(tab);
}
}
// 调整树结构的同时将高位树后移oldCapacity位
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}
3 get()
get()方法可以从HashMap中取出一个键值对
/**
* Returns the value to which the specified key is mapped,
* or {@code null} if this map contains no mapping for the key.
*
* More formally, if this map contains a mapping from a key
* {@code k} to a value {@code v} such that {@code (key==null ? k==null :
* key.equals(k))}, then this method returns {@code v}; otherwise
* it returns {@code null}. (There can be at most one such mapping.)
*
*
A return value of {@code null} does not necessarily
* indicate that the map contains no mapping for the key; it's also
* possible that the map explicitly maps the key to {@code null}.
* The {@link #containsKey containsKey} operation may be used to
* distinguish these two cases.
*
* @see #put(Object, Object)
*/
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
/**
* Implements Map.get and related methods
*
* @param hash hash for key
* @param key the key
* @return the node, or null if none
*/
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// 根据hash计算index,获取到bucket
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// 假如bucket 里面的node list的第一个就是要找的
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// 假如第一个不是,而且有后继结点
if ((e = first.next) != null) {
// 假如是红黑树节点,那么就用树的查找继续查找
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
// 遍历查找之后的节点
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
4 treeifyBin()
将链表转化为红黑树的算法
/**
* Replaces all linked nodes in bin at index for given hash unless
* table is too small, in which case resizes instead.
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// 如果没有初始化,那么先初始化
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
// 取出对应的链表
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
// 挨个替换为树节点
TreeNode<K,V> p = replacementTreeNode(e, null);
// 保存头节点
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
// 截止到这里,还是个链表,没有变成树,只是变成了双向链表
if ((tab[index] = hd) != null)
// 将双向链表转化成树
hd.treeify(tab);
}
}
/**
* Forms tree of the nodes linked from this node.
* @return root of tree
*/
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
// 设置树的根节点,根节点设置为黑色
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
// 向树中插入新节点
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
// 向下查找插入点,如果hash小于根,那么direction=-1,是左边,否则是1,右边
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
// 这里是假如使用了实现了comparable的类的实例作为
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
// 这里根据dir的值选择继续查找的方向,另外判断是否到了该插入的地方
// 如果下一个比较的是null,那么就插入
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 插入之后调节树使之变平衡
root = balanceInsertion(root, x);
break;
}
}
}
}
moveRootToFront(tab, root);
}
/*
* 插入之后的平衡操作
* 红黑树的限制:
* 1. 根节点是黑色
* 2. 每条路径上黑色节点一样多
* 3. 每个叶子节点都是黑色的空节点
* 4. 每个红色节点的两个孩子都必须是黑色的(隐含不能有连续的红色节点)
*/
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// 设置新插入的节点为红节点
x.red = true;
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {
// 如果x是根节点,那么x应该是黑色
x.red = false;
return x;
}
// 如果x的父亲是黑色的或者x的父亲是根节点,那么调整结束,因为此时所有规则都满足了
// 根节点是黑色,这个不变,每条路径上黑色节点也没变,
// 空叶子节点也没变(红色的插在了中间),规则4也没变
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 假如x的父亲是x的祖父的左儿子,并且x的父亲是一个红色节点
if (xp == (xppl = xpp.left)) {
// 如果x的父亲的右兄弟不为空且也是红节点
// 就将x祖父的两个儿子都转为黑色节点,将x的祖父转为红色,并将x的祖父赋值给x,向上递归
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
// 如果x是右孩子,那么就左旋调整
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 如果调整之后x的父亲不为空,即x不是根节点
if (xp != null) {
// 将x的父亲设置为黑节点
xp.red = false;
// 如果x的祖父也不为空,那么继续右旋调整
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
// 如果x的父亲是x的祖父的右孩子
else {
// 如果x的祖父有两个红孩子,那么将x祖父的孩子都设置为黑孩子,x祖父设置为红孩子,
// x祖父赋值给x,向上递归处理
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 如果x的父亲没有兄弟
else {
// 如果x是左孩子,先右旋调整
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 调整完发现x还有父亲,那么将x的父亲设置为黑节点
if (xp != null) {
// 如果x祖父存在,那么左旋调整
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
值得注意的问题
- 扩容之后移动了怎么保证能定位到?
首先看确定bucketIndex的方法:hash&(n-1),n是table长度
由于n是10000···000这样的2的整数次幂,那么n-1是这样的1111···1111
hash和n-1做与操作,得到的是一个模n的余数,接下来看在resize中移动了的值hash有什么特点,那就是hash&n = n,这里的n是未扩容前的容量,假设扩容前n是2的x次幂,那么n的二进制是1000···0,0的个数为x,而满足hash&n = n的hash从低位开始,第x+1位也是1,那么模2n余数必然是n+模n的余数:
即if hash&n = n ;then hash mod 2n = (hash mod n) + n - 为什么要保证大小是2的次方数
首先,计算机以2进制保存数据,使用2的整数次幂可以以较小开销实现除模取余这样的操作。在扩容时操作也更简单。最重要的还是要保证在扩容前后hash分布的均匀度,如果是2的整数次幂,那么只需要简单的将 模2n 大于等于n的移动到后面即可,而若是3倍或5倍这样的增长速度,那么在使现有的数据重新均匀分布在新的表上并保证bucketIndex的计算不受影响将会是一个复杂且耗时的操作。