深度学习多种模型评估指标介绍 - 附sklearn实现

1、准确率accuracy

预测正确的样本数/总样本数，但accuracy对于样本数据不均衡的问题来说不具有说服力，当样本不均衡时，准确率即是很高也不代表分类器效果好

#准确率
from sklearn.metrics import accuracy_score
y_true = [2, 1, 0, 1, 2, 0]
y_pred = [2, 0, 0, 1, 2, 1]
accuracy_score(y_true, y_pred)   #总样本数6个，预测正确了4个，正确率：4/6

在介绍下面的评估指标时，先明白以下概念，在多类分类问题中，分类结果一般有4种情况:

• 属于类C的样本被正确分类到类C，记这一类样本数为 TP
• 不属于类C的样本被错误分类到类C，记这一类样本数为 FP
• 属于类别C的样本被错误分类到类C的其他类，记这一类样本数为 TN
• 不属于类别C的样本被正确分类到了类别C的其他类，记这一类样本数为 FN
  
  

2、精准率precision

预测为正样本中有多少是真正的正样本，精准率看的是预测为某一类的样本中有多少是真正属于这一类的，计算公式：

#精准率
from sklearn.metrics import precision_score
y_true = [1, 1, 1, 1, 1, 0]
y_pred = [1, 0, 0, 1, 1, 1]
#精准率precision: y_pred预测出了四个正例，其中有三个为正例，精准率：3/4=0.75
precision_score(y_true, y_pred)  

3、召回率recall

样本中的正例有多少被预测正确了，召回率看的是在分类任务中某一类样本是否完全被预测正确，计算公式：

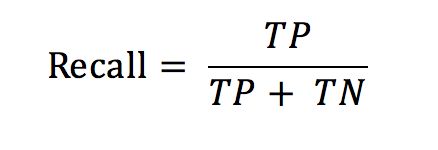
#召回率
from sklearn.metrics import recall_score
y_true = [1, 1, 1, 1, 1, 0]
y_pred = [1, 0, 0, 1, 1, 1]
#召回率recall：总共有五个正例，y_pred预测正确率3个正例，召回率：3/5=0.6
recall_score(y_true, y_pred)

4、F1-Score

精准率和召回率的调和平均值，计算公式：

#f1_score
from sklearn.metrics import f1_score
y_true = [1, 1, 1, 1, 1, 0]
y_pred = [1, 0, 0, 1, 1, 1]
f1_score(y_true, y_pred)  #2*0.75*0.6/(0.75+0.6)=2/3

5、宏平均Macro-average

所有类的F1-Score取算术平均值就是Macro-average

6、微平均Micro-average

微平均即是和准确率是一样的，即正确分类的样本占样本总数的比例

7、常用分类指标classification_report

Sklearn中classification_report函数显示主要分类指标的文本报告，通过打印 classification_report分类文本报告便可知道分类结果中各个类别的精准率、召回率和f1-scort，看下面示例：

#classification_report
from sklearn.metrics import classification_report
y_true = [1, 1, 1, 1, 1, 0]
y_pred = [1, 0, 0, 1, 1, 1]
targets = ['class0', 'class1']
print(classification_report(y_true, y_pred, target_names=targets))

打印结果如下：

8、常用分类指标confusion_matrix

Sklearn中confusion_matrix函数混淆矩阵是机器学习中总结分类模型预测结果，混淆矩阵是展示了真实数据的正负类别和模型预测的分类的正负的类别(可以是多分类)

下面是confusion_matrix从sklearn.metrics调用，直接传入真实标签和预测标签即可

#confusion_matrix
from sklearn.metrics import confusion_matrix
y_true = [1, 1, 1, 1, 1, 0]
y_pred = [1, 0, 0, 1, 1, 1]
print(confusion_matrix(y_true, y_pred))
#打印结果如下：
#[[0 1]
# [2 3]]

上面打印的结果的意思即是下图所示：

9、PR曲线

PR曲线：精确率precision vs 召回率recall 曲线
PR曲线横轴：召回率Recall
PR曲线纵轴：精准率Precision

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import roc_curve, auc
y_true = [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0]
y_pred = [1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1]

#数据量较少，PR曲线效果不明显，可使用在实际大量数据中
precision, recall, pr_thresh = precision_recall_curve(y_true, y_pred)
plt.figure(figsize=(10,5))

plt.subplot(1, 2, 1)
plt.step(recall, precision, color='b', alpha=0.2, where='post')
plt.fill_between(recall, precision, step='post', alpha=0.2, color='b')
plt.grid(linestyle='--')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.01])
plt.xlim([0.0, 1.0])
# create the axis of thresholds (scores)
ax2 = plt.gca().twinx()
ax2.plot(recall[1:], pr_thresh, markeredgecolor='r',linestyle='dashed', color='r')
ax2.set_ylabel('Threshold',color='r')
ax2.set_ylim([0.0, 1.0])
ax2.set_xlim([0.0, 1.0])
plt.title('Precision-recall curve')
plt.show()

下面是上述代码运行结果图，在实际中ROC曲线对于分类结果的衡量比PR曲线效果好，在下面一节中介绍原因：

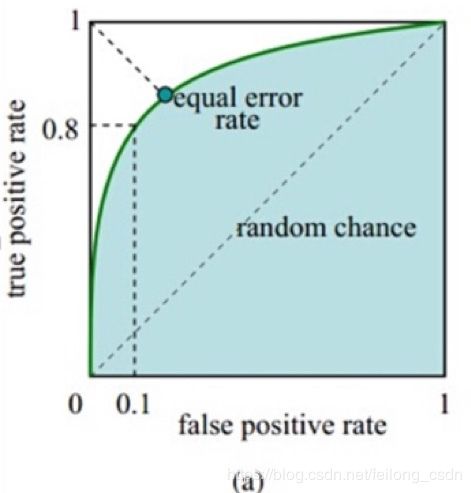
10、ROC曲线、AUC值

roc曲线： 接收者操作特征receiver operating characteristic，roc曲线上每个点反应着对同一个信号刺激的感受性
roc曲线横轴： 负正类率FPR代表分类器预测的正类中实际负实例占所有负实例的比例
roc曲线纵轴： 真正类率TPR代表分类器预测的正类中实际正实例占所有正实例的比例

例如我们设定一个阈值为0.6，概率大于等于0.6的为正例，小于0.6的为负例。对应的就可以算出一组(FPR,TPR)，在平面中得到对应的坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大，阈值最大时，对应坐标点为(0, 0)，阈值最小时，对应坐标点为(1,1)

横轴FPR越大，预测正类中实际负类越多，纵轴TPR越大，预测正类中实际正类越多
对于roc曲线的理想目标，TPR=1，FPR=0，即图中的(0,1)点，故roc曲线越靠拢(0,1)点，越偏离45度对角线越好。

AUC值： ROC曲线下的面积，介于0.1和1之间，AUC作为数值可以直观的评价分类器的好坏，值越大越好，首先AUC值是一个概率值，当你随机挑选一个正样本及负样本，当前的分类算法根据计算得到的score值将这个正样本排在负样本前面的概率值就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好的分类

如何绘制ROC曲线： 通过模型预测样本为正例的概率值，然后通过阈值进行划分样本预测为正负例的情况，对于每一个阈值计算一个TPR真正类率和FPR负正类率，使用TPR作为纵轴，FPR作为横轴进行ROC曲线的绘制

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import roc_curve, auc
y_true = [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0]
y_pred = [1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1]
precision, recall, pr_thresh = precision_recall_curve(y_true, y_pred)
plt.figure(figsize=(10,5))
fpr, tpr, thresholds = roc_curve(y_true, y_pred)
roc_auc = auc(fpr, tpr)

# plt.figure()
plt.subplot(1, 2, 2)
lw = 2
plt.plot(fpr, tpr, color='darkorange', lw=lw, label='ROC curve (AUC = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.fill_between(fpr, tpr, step='post', alpha=0.2, color='darkorange')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate (Recall)')
plt.legend(loc="lower right")
plt.grid(linestyle='--')

# create the axis of thresholds (scores)
ax2 = plt.gca().twinx()
ax2.plot(fpr, thresholds, markeredgecolor='r',linestyle='dashed', color='r')
ax2.set_ylabel('Threshold',color='r')
ax2.set_ylim([0, 1])
ax2.set_xlim([0, 1])
plt.title('ROC curve')
plt.tight_layout()

plt.show()

下面是上述代码运行结果图：

为什么使用ROC和AUC评价分类器
既然已经这么多标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变换的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡，即正负样本比例差距较大，而且测试数据中的正负样本也可能随着时间变化。下图是ROC曲线和Presision-Recall曲线的对比：

在上图中，(a)和©为Roc曲线，(b)和(d)为Precision-Recall曲线。
(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果，©(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果，可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线变化较大

总结：PR曲线和ROC曲线的区别
PR曲线即是recall召回率作为横轴，精准率precision作为纵轴
召回率指的是预测为正样本中预测正确的正样本数占实际总正样本数的比例
精准率指的是预测为正样本中预测正确的正样本数占总预测为正样本的比例

ROC曲线的横轴是预测为正样本中的实际负例占实际所有负例的比例
ROC曲线的纵轴是预测为正样本中实际正例占实际所有正例的比例，因此ROC曲线和PR曲线是不同的，但曲线都是根据不同阈值进行划分的