《编程之美》学而思-中国象棋将帅问题

中国象棋将帅问题

flyfish 2015-8-11

问题引自 《编程之美》中国象棋将帅问题
将帅每一着只许走一步，前进、后退、横走都可以，但不能走出“九宫”，被限制在3×3的格子里运动。将和帅不准在同一直线上直接对面。
请写出一个程序，输出将帅所有合法的位置，要求在代码中只能使用一个变量.
约定用a表示“将”，b表示“帅”

一个解法是关于位操作 跳过

原文提供解法一

struct {
    unsigned char a:4;
    unsigned char b:4;
} i;

    for(i.a = 1; i.a <= 9;i.a++)
        for(i.b = 1;i.b <=9;i.b++)
            if(i.a % 3 != i.b % 3)
                printf("A=%d,B=%d\n",i.a,i.b);

思路是将一个变量拆成两部分

原文提供解法二

BYTE i = 81;
while (i--)
{
    if (i / 9 % 3 == i % 9 % 3)
        continue;
    printf ("A = %d, B = %d\n", i / 9 + 1, i % 9 + 1);
}

问题转换
有个两位数m，十位上的数是a,个位上是b
每个位上的数只能是从1到9组成,则共有9*9=81种组成方式

a[1,9]={a|1⩽a⩽9}
b[1,9]={b|1⩽b⩽9}

两位数数列
11、12、13、14、15、16、17、18、19
21、22、23、24、25、26、27、28、29
…

当下标从0开始时,各个数就减1， 就完全成了一个9进制的数，满9进1
10、11、12、13、14、15、16、17、18
20、21、22、23、24、25、26、27、28
…

10进制的81 ，9进制也就是100
9进制表示

十位数= m / 9
个位数= m % 9

将帅只有3列可移动，将帅不能位于同一列也就是共有9*（9-3）=54种组成方式

a%3 != b%3

因为下标从0开始时,各个数已经减1，输出时需要加1
m / 9 + 1
m % 9 + 1

关于循环
1 两位数最大99 所以循环可以从99开始递减
2 每个位上的数只能是从1到9组成有81种方式，则可以从81开始递减
3 合法的位置有54种，所以可以从54开始递减
4 当前a和b的位置符合条件的话，那么将a，b位置对调之后的位置也符合条件，则可以将循环从27开始

循环从54开始，以三进制输出

        BYTE i=54;
        while (i--)
        {
            printf("A = %d%d,",i/18,i%18/6);
            printf("B = %d%d\n",i%3,(( (i%6/3+i%18/6) %3 +1)%3));
        }

图中3进制 由两位组成，别表示行和列

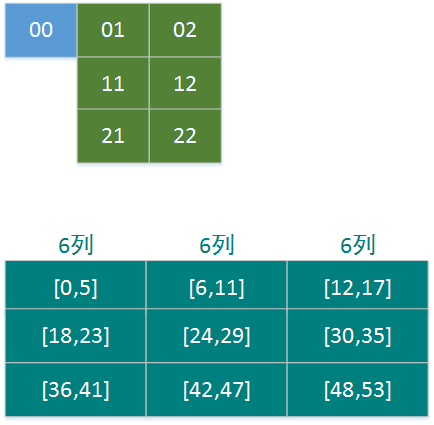
像这样A的一个位置，对应B的6个位置
A的1列有3个位置，每个位置可对应B的6个位置，共3*6=18个位置

0行 A[0,17]
1行 A[18,35]
2行 A[36,53]

A的行 i/18
A的列 i%18/6

B的行 i%3
B的列 ((i%6/3+i%18/6) %3 +1)%3

如果循环从27开始时，需要在while 循环中再加两行printf