信息熵、交叉熵与相对熵(KL散度)的关系，还介绍了联合信息熵和条件熵、互信息（信息增益）的概念

@(关于机器学习的其他)[KL散度][信息熵][交叉熵]

---

1、信息量

信息量用一个信息所需要的编码长度来定义,而一个信息的编码长度跟其出现的概率呈负相关,因为一个短编码的代价也是巨大的,因为会放弃所有以其为前缀的编码方式,比如字母”a”用单一个0作为编码的话,那么为了避免歧义,就不能有其他任何0开头的编码词了.所以一个词出现的越频繁,则其编码方式也就越短,同时付出的代价也大.

其实也就可以说一件事情发生概率很小的话，那么当他发生的时候所代表的信息量也更大

I=log2(1p(x))=−log2(p(x)) I = l o g 2 ( 1 p ( x ) ) = − l o g 2 ( p ( x ) )

2、信息熵

而信息熵则代表一个分布的信息量,或者编码的平均长度

1. 信息熵代表的是随机变量或整个系统的不确定性，熵越大，随机变量或系统的不确定性就越大。也就是信息量的一个总期望值也叫均值
2. 根据真实分布，我们能够找到一个最优策略，以最小的代价消除系统的不确定性，而这个代价大小就是信息熵
3. 信息熵衡量了系统的不确定性，而我们要消除这个不确定性，所要付出的【最小努力】（猜题次数、编码长度等）的大小就是信息熵

H(p)=∑xp(x)log2(1p(x))=∑xp(x)log2(p(x)) H ( p ) = ∑ x p ( x ) l o g 2 ( 1 p ( x ) ) = ∑ x p ( x ) l o g 2 ( p ( x ) )

3、交叉熵cross-entropy

交叉熵本质上可以看成,用一个猜测的分布的编码方式去编码其真实的分布,得到的平均编码长度或者信息量

交叉熵，用来衡量在给定的真实分布 p p 下，使用非真实分布 q q 所指定的策略消除系统的不确定性所需要付出的努力的大小
交叉熵越低，这个策略就越好，最低的交叉熵也就是使用了真实分布所计算出来的信息熵，因为此时 ，交叉熵 = 信息熵。这也是为什么在机器学习中的分类算法中，我们总是最小化交叉熵，因为交叉熵越低，就证明由算法所产生的策略最接近最优策略，也间接证明我们算法所算出的非真实分布越接近真实分布。

Hp(q)=∑xp(x)log2(1q(x)) H p ( q ) = ∑ x p ( x ) l o g 2 ( 1 q ( x ) )

3.1 交叉熵 cross-entropy在机器学习领域的作用

交叉熵cross-entropy在机器学习领域中经常作为最后的损失函数
为什么要用cross-entropy呢，根据上面的解释，他本质上相当于衡量两个分布之间的距离，因为只有当猜测的分布约接近于真实分布，则其值越小，下确界为真是分布计算的信息熵大小。

L=−∑iyilog(p(xi))+(1−yi)log(1−p(xi)) L = − ∑ i y i l o g ( p ( x i ) ) + ( 1 − y i ) l o g ( 1 − p ( x i ) )

在LR中用cross-entry比平方误差方法好在：
1. 在LR中，如果用平方损失函数，则损失函数是一个非凸的，而用cross-entropy的话就是一个凸函数
2. 用cross-entropy做LR求导的话，得到的导数公式如下

∂L∂θj=−∑i(yi−p(xi))xij ∂ L ∂ θ j = − ∑ i ( y i − p ( x i ) ) x i j

而用平方损失函数的话，其求导结果为:

∂L∂θj=−∑i(yi−p(xi))p′(xi) ∂ L ∂ θ j = − ∑ i ( y i − p ( x i ) ) p ′ ( x i )

平方损失函数中会出现 p′(xi) p ′ ( x i ) 而sigmoid函数的导数会出现梯度消失的问题

4、相对熵（KL散度）

KL散度/距离是衡量两个分布的距离,KL距离一般用 D(p||q) D ( p | | q ) 或者 Dp(q) D p ( q ) 称之为 p p 对 q q 的相对熵

Dp(q)=Hp(q)−H(p)=∑xp(x)log2(p(x)q(x)) D p ( q ) = H p ( q ) − H ( p ) = ∑ x p ( x ) l o g 2 ( p ( x ) q ( x ) )

4.1 相对熵（KL散度）与cross-entropy的关系

即：相对熵 = 某个策略的交叉熵 - 信息熵
由之前分析易知此衡量指标的下确界为0，因为交叉熵最小等于信息熵

4.2 相对熵（KL散度）非负性证明

利用琴生不等式：

Dp(q)=∑xp(x)log2(p(x)q(x)) D p ( q ) = ∑ x p ( x ) l o g 2 ( p ( x ) q ( x ) )

=−∑xp(x)log2(q(x)p(x)) = − ∑ x p ( x ) l o g 2 ( q ( x ) p ( x ) )

=−E(log2(q(x)p(x))) = − E ( l o g 2 ( q ( x ) p ( x ) ) )

≥log2E(q(x)p(x)) ≥ l o g 2 E ( q ( x ) p ( x ) )

=log2∑xp(x)(q(x)p(x)) = l o g 2 ∑ x p ( x ) ( q ( x ) p ( x ) )

=log2∑xq(x) = l o g 2 ∑ x q ( x )

因为 ∑xq(x)=1 ∑ x q ( x ) = 1
所以上式

Dp(q)≥0 D p ( q ) ≥ 0

非负性证明完成

5、联合信息熵和条件信息熵

下面我们要说的是联合分布中（即同一个分布中）的两个变量相互影响的关系，上面说的KL和cross-entropy是两个不同分布之间的距离度。

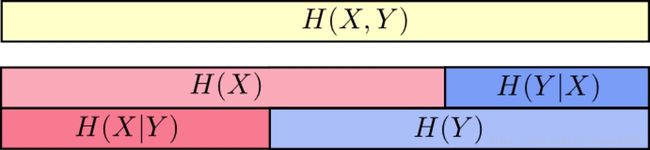
联合信息熵：

H(X,Y)=∑x,yp(x,y)log2(1p(x,y)) H ( X , Y ) = ∑ x , y p ( x , y ) l o g 2 ( 1 p ( x , y ) )

条件信息熵：

H(X|Y)=∑yp(y)∑xp(x|y)log2(1p(x|y)) H ( X | Y ) = ∑ y p ( y ) ∑ x p ( x | y ) l o g 2 ( 1 p ( x | y ) )

=∑x,yp(x,y)log2(1p(x|y)) = ∑ x , y p ( x , y ) l o g 2 ( 1 p ( x | y ) )

举个例子，更容易理解一些，比如天气是晴天还是阴天，和我穿短袖还是长袖这两个事件其可以组成联合信息熵 H(X,Y) H ( X , Y ) ，而对于 H(x) H ( x ) 就是天气单独一个事件的信息熵，因为两个事件组合起来的信息量肯定是大于单一一个事件的信息量的。
而今天天气和我今天穿衣服这两个随机概率事件并不是独立分布的，所以如果已知今天天气的情况下，我的穿衣与天气的联合信息量/不确定程度是减少了的，也就相当于两者联合信息量已知了今天下雨，那么 H(x) H ( x ) 的信息量就应该被减去，得到当前的新联合信息量，也相当于条件信息量。
所以当已知 H(x) H ( x ) 这个信息量的时候，联合分布 H(X,Y) H ( X , Y ) 剩余的信息量就是条件熵：

H(Y|X)=H(X,Y)−H(X) H ( Y | X ) = H ( X , Y ) − H ( X )

根据上面那个图，也可以通俗的理解为已知X的情况下，H(X,Y)剩余的信息量

6、互信息（信息增益）

互信息就是一个联合分布中的两个信息的纠缠程度/或者叫相互影响那部分的信息量

I(X,Y)=H(X)+H(Y)−H(X,Y) I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y )

I(X,Y)=H(Y)−H(Y|X) I ( X , Y ) = H ( Y ) − H ( Y | X )

决策树中的信息增益就是互信息，决策树是采用的上面第二种计算方法，即把分类的不同结果看成不同随机事件Y，然后把当前选择的特征看成X，则信息增益就是当前Y的信息熵减去已知X情况下的信息熵。

通过下图的刻画更为直观一些

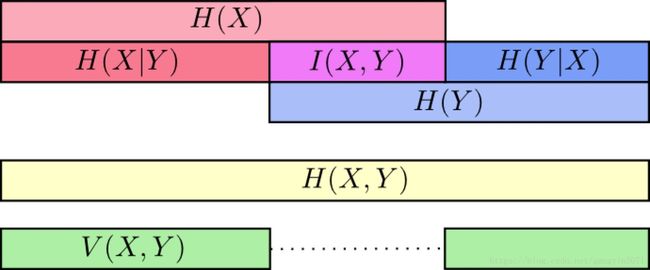
以上图可以清楚的看到互信息 I(X,Y) I ( X , Y ) 的不同求法
这里还有另外一个量叫variation of information【不知道中文名叫啥】

V(X,Y)=H(X,Y)−I(X,Y) V ( X , Y ) = H ( X , Y ) − I ( X , Y )

Variation of information度量了不同随机变量之间的差别，如果V(X,Y)=0说明这两个变量是完全一致的，其约大说明两个变量越独立。
这里再注意一下Variation of information和KL距离的差别：
Variation of information是联合分布中（即同一个分布中）的两个变量相互影响的关系
KL和cross-entropy是两个不同分布之间的距离度量

6.1 非负性证明

I(X,Y)=H(X)+H(Y)−H(X,Y) I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y )

=−∑x,yp(x,y)(log(p(x))+log(p(y))−log(p(x,y))) = − ∑ x , y p ( x , y ) ( l o g ( p ( x ) ) + l o g ( p ( y ) ) − l o g ( p ( x , y ) ) )

=−∑x,yp(x,y)(log(p(x)p(y)p(x,y))) = − ∑ x , y p ( x , y ) ( l o g ( p ( x ) p ( y ) p ( x , y ) ) )

=D(P(X,Y)||P(X)P(Y)) = D ( P ( X , Y ) | | P ( X ) P ( Y ) )

即互信息可以转化成两个分布 P(X,Y) P ( X , Y ) 和 P(X)P(Y) P ( X ) P ( Y ) 之间的KL距离，而KL距离的非负性在上面已经被证明过了，所以

I(X,Y)≥0 I ( X , Y ) ≥ 0

参考资料：

[1] 国外博客：http://colah.github.io/posts/2015-09-Visual-Information/
[2] csdn博客：https://blog.csdn.net/haolexiao/article/details/70142571
[3] 知乎回答：https://www.zhihu.com/question/41252833