|【c++】|——普及转提高测试——||
朴 实 无 华 的 正 文 分 割 线
第一题
立方数(cubic)
题目描述
输入格式(cubic.in)
第一行一个数T,表示有T组数据。
接下来T行,每行一个数P。
输出格式(cubic.out)
输出T行,对于每个数如果是立方数,输出“YES”,否则输出“NO”。
输入样例
3
8
27
28
输出样例
YES
YES
NO
数据范围
对于30%的数据p<=100。
对于60%的数据p<=10^6。
Ok
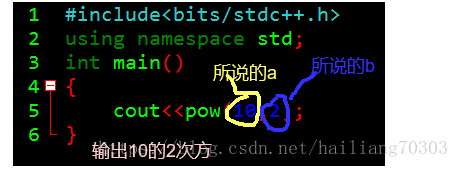
那么想必sqrt大家也都知道吧。不过我觉得还是再讲一下
2.sqrt:
求a的根号

那么这些符号都知道了的话,我对这题就开挂做了哦
请欣赏整个班最短的代码!
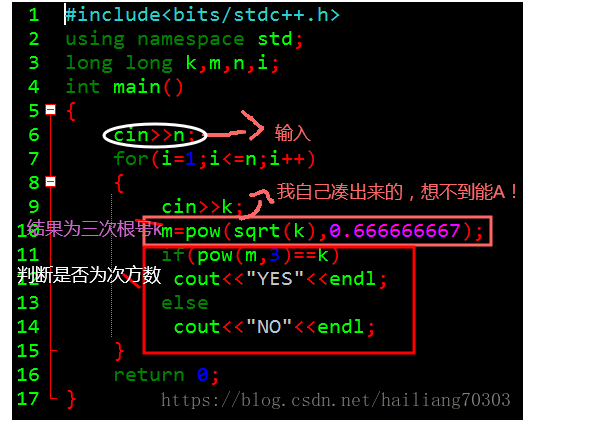

我真帅啊
第六题//都说先讲我A的了
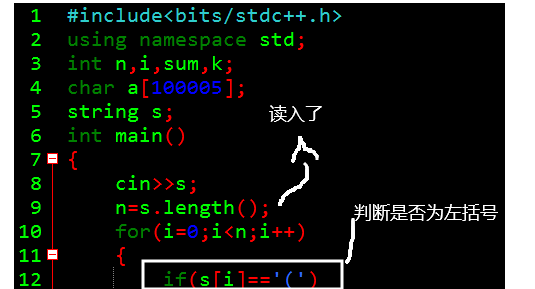
括号(shower)
Time Limit:1000ms Memory Limit:128MB
【问题描述】
有一段括号序列,将一个括号修改成为可以成功的如()((最右边括号不行,于是乎,做一次操作,求最小代价使得括号序列合法。
【输入格式】
一行一个括号序列。
【输出格式】
一行一个整数代表答案。
【样例输入】
())(
【样例输出】
2
【数据范围与规定】
对于50%的数据,括号序列长度不超过100。
对于 100% 的数据,括号序列长度不超过 10 5 且一定为偶数,只包含小括号。下面,是第二题
第二题
立方差数
Time Limit:1000ms Memory Limit:128MB
题目描述
若一个数可以被写作是两个立方数的差,且p是质数,则这个数就是“立方差数”,例如7(8-1),26(27-1),19(27-8)都是立方差数。
输入格式(cubicp.in)
第一行一个数T,表示有T组数据。
接下来T行,每行一个质数P。
输出格式(cubicp.out)
输出T行,对于每个数如果是立方差数,输出“YES”,否则输出“NO”。
输入样例
5
2
3
5
7
11
输出样例
NO
NO
NO
YES
NO
数据范围
对于30%的数据p<=100。
对于60%的数据p<=10^6。
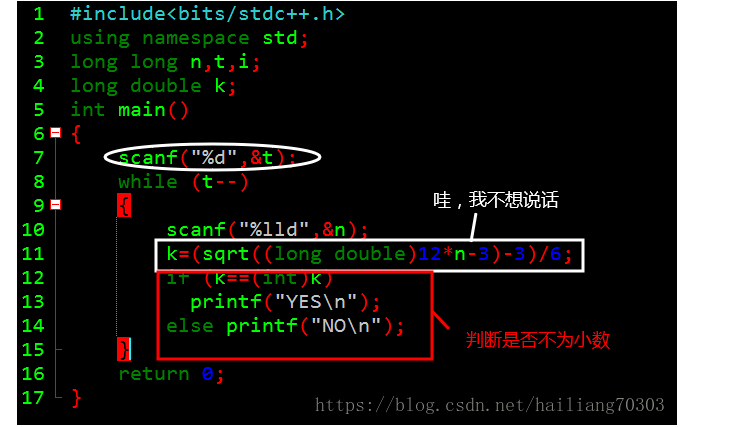
对于100%的数据p<=10^12,T<=100。枚举
注意,如果没有p是素数这个条件,我们的枚举将会变得复杂,复杂度也会升高。
立方差公式。 我当时怎么就没想到呢
p=a^3-b^3=(a-b)*(a^2+a*b+b^2)
这样一来,枚举就变得十分简单。
但是还可以发现这个高效率的:k=(sqrt((long double)12*n-3)-3)/6;
所以请观赏
哇哇哇哇哇
下一题是水题
第四题
水题(water)
Time Limit:1000ms Memory Limit:128MB
题目描述
有两副牌,每副牌都有n张。
对于第一副牌的每张牌长和宽分别是xi和yi。对于第二副牌的每张牌长和宽分别是aj和bj。第一副牌的第i张牌能覆盖第二副牌的第j张牌当且仅当xi>=aj并且yi>=bj。(注意牌不能翻转)当然一张牌只能去覆盖最多一张牌,而不能覆盖好多张。
让两副牌的各n张一一对应叠起来。第二副牌最多有几张能被第一副牌所覆盖。
输入格式(water.in)
第一行一个数n。
接下来n行,每行两个数xi,yi。
接下来n行,每行两个数aj,bj。
输出格式(water.out)
输出答案。
输入样例
3
2 3
5 7
6 8
4 1
2 5
3 4
输出样例
2
数据范围
对于50%的数据n<=10。
对于80%的数据n<=1000。
对于100%的数据1<=n<=100000,1<=xi,yi,aj,bj<=10^9。
对x[i]从小到大进行排序。 每次遇到B类牌,将y值插入进某个数据结构中
遇到A类牌(不考虑x),找这个数据结构中y值尽可能大且不超过这张牌的y值
那么看我们是要用到一个不遗漏的数组multiset(这个我不会讲,所以请看点击打开链接)
OK,我其实还是没有真正理解透,有些可能不是很明白,请谅解。大佬可以自行分析啊。
那么这既然是普及转提高,虽无图论,但dp还是要有的
第三题
梦境(dream)
Time Limit:1000ms Memory Limit:128MB
题目描述
x一定是1~n之间的正整数。恰好要x金币。但只有若干的金币,每个金币都价值一定数量的钱(注意任意两枚金币所代表的钱一定是不同的,且这个钱的个数一定是正整数)。带最少的金币,使得对于任意x,都能恰好拼出这么多钱。并且有多少携带金币的方案总数。
具体可以看样例。
输入格式(dream.in)
第一行一个数n,如题意所示。
输出格式(dream.out)
输出两个数,第一个数表示GTW至少携带的金币个数,第二数表示方案总数。
输入样例
6
输出样例
3 2
样例解释
GTW需要至少带3枚金币,有两种方案,分别是{1,2,3},{1,2,4}来恰好得到任意的1~n之间的x。
输入样例2
10
输出样例2
4 8
数据范围
对于30%的数据n<=10。
对于60%的数据n<=100。
对于100%的数据n<=1000。
第一问是个找规律题,很容易发现min = log2(n)
第二问动态规划,四重循环,dp[i][j][k] 当前有i个金币,金币和是j,最大的金币k,那么考虑下一次会拿多大面值的金币,显然有f[i+1][min(n,j+l)][l]+=f[i][j][k](k<l≤j+1)但是这样开不下数组,所以滚动数组优化一下 最大的金币k只是不知道会不会超时(当然不超)
来来来,终于是最后一题了
猜数字(number)
Time Limit:1000ms Memory Limit:128MB
题目描述
总共有n个互不相同的正整数,每次猜一段区间的最小值。形如[li,ri]这段区间的数字的最小值一定等于xi。
我们总能构造出一种方案满意。直到……自己猜的就是矛盾的!
例如猜[1,3]的最小值是2,[1,4]的最小值是3,这显然就是矛盾的。
你需要告诉,它第几次猜数字开始就已经矛盾了。
输入格式(number.in)
第一行两个数n和T,表示有n个数字,猜了T次。
接下来T行,每行三个数分别表示li,ri和xi。
输出格式(number.out)
输出一个数表示第几次开始出现矛盾,如果一直没出现矛盾输出T+1。
输入样例
20 4
1 10 7
5 19 7
3 12 8
1 20 1
输出样例
3
数据范围
对于50%的数据n<=8,T<=10。
对于80%的数据n<=1000,T<=1000。
对于100%的数据1<=n,T<=1000000,1<=li<=ri<=n,1<=xi<=n(但并不保证一开始的所有数都是1~n的)。
这题还望大佬指点一下,思路是二分答案,只是不知是哪儿错了?
#include
using namespace std;
struct ss
{
int l,r,x;
}a[1000010],b[1000010];
int n,t,ans,i,j,f[1000010],l=1,r,mid,minn,maxx,minm,maxn;
bool myc(ss xx,ss yy)
{
return xx.x>yy.x;
}
int zhao(int x)
{
if(f[x]==x)
return x;
else
return f[x]=zhao(f[x]);
}
bool work(int k)
{
for(i=0;i<=n+1;i++)
f[i]=i;
for(i=1;i<=k;i++)
b[i]=a[i];
sort(b+1,b+k+1,myc);
minn=b[1].l,maxx=b[1].l,minm=b[1].r,maxn=b[1].r;
for(int i=2;i<=k;i++)
if(b[i].xminm)
return true;
for(j=zhao(minn);j<=maxn;j++)
f[zhao(j)]=zhao(maxn+1);
minn=maxx=b[i].l,minm=maxn=b[i].r;
}
else
{
minn=min(minn,b[i].l),
maxx=max(maxx,b[i].l),
minm=min(minm,b[i].r),
maxn=max(maxn,b[i].r);
if(maxx>minm)
return true;
}
if(zhao(maxx)>minm)
return true;
return false;
}
int main()
{
cin>>n>>t;
for(int i=1;i<=t;i++)
scanf("%d",a[i].l),scanf("%d",a[i].r),scanf("%d",a[i].x);
ans=t+1,r=t;
while(l+1 谢谢观赏啊