R语言进行数据预处理
4.R语言进行数据预处理
在实际情况下,数据通常是不完整(缺少属性值或某些感兴趣的属性,或仅包含聚集数据)、含噪声(包含错误或存在偏离期望的离群值)、不一致的,这样的数据必须经过预处理,剔除其中的噪声,回复数据的完整性和一致性后才能使用数据挖掘技术进行分析。
使用mice软件包中的示例数据nhanes2来进行演示。加载mice包前,要先加载lattice,MASS, nnet包:
install.packages("lattice")
install.packages("MASS")
install.packages("nnet")
library(lattice)
library(MASS)
library(nnet)
install.packages("mice")
library(mice)
data(nhanes2)
缺失值处理
判断是否存在缺失值:
> sum(is.na(nhanes2)) #计算nhanes2中缺失值数量
[1] 27
>
>sum(complete.cases(nhanes2)) #计算nhanes2中完整样本的数量
[1] 13
> md.pattern(nhanes2)
age hyp bmi chl
13 1 1 1 1 0
1 1 1 0 1 1
3 1 1 1 0 1
1 1 0 0 1 2
7 1 0 0 0 3
0 8 9 1027
其中1表示没有缺失数据,0表示存在缺失数据。
1. 直接删除法
这种方法最为简单有效,但前提是缺失数据的比例较少,且缺失数据是随机出现的,这样删除数据后对分析影响不大。
2. 随机插补法
从整体中随机抽取某个样本代替缺失样本。
> #随机插补法
> sub =which(is.na(nhanes2[,4]) == TRUE) #返回nhanes2数据集中第4列为NA的行
> dataTR =nhanes2[-sub,] #将第4列不为NA的数据存数dataTR中
> dataTE =nhanes2[sub,] #将第4列为NA的数据存入dataTE
> dataTE[,4] =sample(dataTR[,4],length(dataTE[,4]),replace=T) #在非缺失值中简单抽样
> dataTE
age bmi hyp chl
1 20-39 NA
4 60-99 NA
10 40-59 NA
11 20-39 NA
12 40-59 NA
15 20-39 29.6 no 187
16 20-39 NA
20 60-99 25.5 yes 284
21 20-39 NA
24 60-99 24.9 no 238
3. 均值法
均值法通过计算缺失值所在变量所有非缺失值的均值,使用均值来代替缺失值。优点:不会减少信息,处理简单;缺点:当缺失值数据不是随机出现时会产生偏差。
> #均值法
> sub =which(is.na(nhanes2[,4]) == TRUE) #返回nhanes2数据集中第4列为NA的行
> dataTR =nhanes2[-sub,] #将第4列不为NA的数据存数dataTR中
> dataTE =nhanes2[sub,] #将第4列为NA的数据存入dataTE
> dataTE[,4] =mean(dataTR[,4]) #用非缺失值的均值代替缺失值
> dataTE
age bmi hyp chl
1 20-39 NA
4 60-99 NA
10 40-59 NA
11 20-39 NA
12 40-59 NA
15 20-39 29.6 no 191.4
16 20-39 NA
20 60-99 25.5 yes 191.4
21 20-39 NA
24 60-99 24.9 no 191.4
4. 回归模型插补法
由于随机插补和均值插补中没有利用相关变量信息,因此会存在一定偏差,而回归模型是将需要插补变量作为因变量,其他相关变量作为自变量,通过建立回归模型预测出因变量的值对缺失变量进行插补。
> #回归模型插补法
> sub =which(is.na(nhanes2[,4]) == TRUE) #返回nhanes2数据集中第4列为NA的行
> dataTR =nhanes2[-sub,] #将第4列不为NA的数据存数dataTR中
> dataTE =nhanes2[sub,] #将第4列为NA的数据存入dataTE
>
> lm =lm(chl~age,data=dataTR) #利用dataTR中age为自变量,chl为因变量构建线性回归模型lm
> dataTE[,4] =round(predict(lm,dataTE)) #按模型lm对dataTE中的缺失值进行预测
> dataTE
age bmi hyp chl
1 20-39 NA
4 60-99 NA
10 40-59 NA
11 20-39 NA
12 40-59 NA
15 20-39 29.6 no 169
16 20-39 NA
20 60-99 25.5 yes 225
21 20-39 NA
24 60-99 24.9 no 225
5. 热平台插补
在非缺失值所在的样本中找到一个与缺失值所在样本相似的样本(匹配样本),利用其观测值对缺失值进行插补。
> #热平台插补
> accept =nhanes2[which(apply(is.na(nhanes2),1,sum) !=0),] #存在缺失值的样本
> donate =nhanes2[which(apply(is.na(nhanes2),1,sum) ==0),] #不存在缺失值的样本
> accept[1,]
age bmi hyp chl
1 20-39 NA
> donate[1,]
age bmi hyp chl
2 40-59 22.7 no 187
上述程序按照样本中是否含有缺失值将nhanes2分成存在缺失值和无缺失值两个数据表。对于accept中的每个样本,热平台插补就是在donate中找到与该样本相似的样本,用相似样本的对应值代替该样本的缺失值。如,对于accept中的第二个样本,插补方法如下:
> #对accept第二个样本进行热平台插补
> accept[2,]
age bmi hyp chl
3 20-39 30.1 no 187
> sa =donate[which(donate[,1]==accept[2,1]&donate[,3]==accept[2,3]&donate[,4]==accept[2,4]),]
> sa
age bmi hyp chl
8 20-39 30.1 no 187
> accept[2,2] =sa[1,2] #用找到的样本替代缺失值
> accept[2,]
age bmi hyp chl
3 20-3930.1 no 187
实际操作中,尤其当变量数量很多时,通常很难找到与需要插补样本完全相同的样本,此时可以看做某些变量将数据分成,在层中对缺失值进行均值插补,即采取冷平台插补方法。
6. 冷平台插补
> #5冷平台插补
> level1<-nhanes2[which(nhanes2[,3]=="yes"),] #按照变量hyp分层
> level1
age bmi hyp chl
14 40-59 28.7 yes 204
17 60-99 27.2 yes 284
18 40-59 26.3 yes 199
20 60-99 25.5 yes NA
> level1[4,4] =mean(level1[1:3,4]) #用层内均值代替第4个样本缺失值
> level1
age bmi hyp chl
14 40-59 28.7 yes 204
17 60-99 27.2 yes 284
18 40-59 26.3 yes 199
20 60-99 25.5 yes 229
噪声数据处理
噪声是一个测量变量中的随机错误或偏差,包括错误值或偏离期望的孤立点值。在R中可以通过调用outliers软件包中的outlier函数寻找噪声数据,该函数通过寻找数据集中与其他观测值及均值差距最大的点作为异常值。
outlier(x, opposite = FALSE, logical =FALSE)
x: 一个数据,通常是一个向量,如果x输入的是一个数据框或矩阵,则outlier函数将逐列算出;
opposite: 默认为FALSE,当为TRUE时,给出相反值;
logical: 默认为FALSE,当为TRUE时,给向量赋予逻辑值,可能为噪声的位置用TRUE表示。
#outlier函数
install.packages("outliers")
> library(outliers)
>set.seed(1);s1=.Random.seed #设置随机数种子,保证每次出现的随机数相同
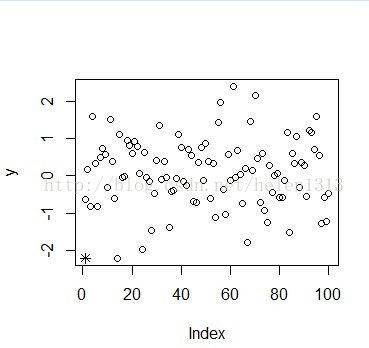
> y=rnorm(100) #生成100个标准正太随机数
> outlier(y)
[1] -2.2147
> plot(y)
>points(-2.2147,pch=8) #用星号标记离群值
离群点检测还可以通过聚类方法进行检测。
在进行噪声检查后,常用分箱、回归、计算机检查和人工检查结合等方法“光滑”数据,去掉数据中的噪声。
数据集成
数据集成是指将多个数据源中的数据合并,存放到一个一致的数据存储中。
在数据集成时,首先要考虑如何对多个数据集进行匹配。
冗余是数据集成的另一个重要问题,可用相关性对数据集冗余进行检测。给定的两个属性,对于定性数据,可以使用卡方检验,对于定量数据,使用相关系数和协方差。
> #卡方检验
>x=cbind(sample(c(1:50),10),sample(c(1:50),10))
> chisq.test(x)
Pearson's Chi-squared test
data: x
X-squared = 54.2495, df = 9, p-value =1.692e-08
P-value<0.05,即在0.05显著性水平下拒绝相关的原假设,即变量不相关。
对于定量数据的相关系数,若两个属性的相关系数为0,表示两个属性独立,不存在相关性;相关系数小于0,负相关;相关系数大于0,正相关;相关系数绝对值越大,相关性越强。
协方差为正,说明两个属性趋向于一起改变,协方差为负,则表示两个属性趋向于相反方向改变。
> #相关系数,协方差
> x=cbind(rnorm(10),rnorm(10))
> cor(x)
[,1] [,2]
[1,] 1.0000000 -0.3908889
[2,] -0.3908889 1.0000000
> cov(x)
[,1] [,2]
[1,] 0.3052548 -0.1413724
[2,] -0.1413724 0.4285095
除了检测属性间的冗余外,还应该检测观测值是否存在重复。
> #查重
> x = cbind(sample(c(1:10),10,replace=T),rnorm(10))
> #随机生成数据集,第一列为样本编号,存在重复
> head(x)
[,1] [,2]
[1,] 10 -0.03472603
[2,] 2 0.78763961
[3,] 6 2.07524501
[4,] 4 1.02739244
[5,] 7 1.20790840
[6,] 3 -1.23132342
> y=unique(x[,1]) #将样本编号去重
> x=x[y,]
> head(x)
[,1] [,2]
[1,] 8 0.5210227
[2,] 2 0.7876396
[3,] 3 -1.2313234
[4,] 4 1.0273924
[5,] 5 0.9838956
[6,] 6 2.0752450