雅克比迭代算法
From https://blog.csdn.net/weixin_33895016/article/details/86031039
雅克比迭代,一般用来对线性方程组,进行求解。形如:
a11∗x1+a12∗x2+a13∗x3=b1a11∗x1+a12∗x2+a13∗x3=b1
a21∗x1+a22∗x2+a23∗x3=b2a21∗x1+a22∗x2+a23∗x3=b2
a31∗x1+a32∗x2+a33∗x3=b3a31∗x1+a32∗x2+a33∗x3=b3
我们需要求解出x1x1 ,x2x2 ,x3x3,我们对这组方程进行变换:
x1=1a11(b1−a12∗x2−a13∗x3)x1=1a11(b1−a12∗x2−a13∗x3)
x2=1a21(b2−a21∗x1−a23∗x3)x2=1a21(b2−a21∗x1−a23∗x3)
x3=1a31(b3−a31∗x1−a32∗x2)x3=1a31(b3−a31∗x1−a32∗x2)
我们不妨假设 x00=(X01,X02,X03)x00=(X10,X20,X30) ,当我们代入上述公式的时候,我们就会得到一组新的 x10=(X11,X12,X13)x01=(X11,X21,X31) ,此刻我们称之为一次迭代.
然后我们将得到的X1,X2,X3再次代入公式,我们将会得到第二次迭代, 当我们重复这种迭代的时候,我们会得到第K次迭代:
xk=(Xk1,Xk2,Xk3)xk=(X1k,X2k,X3k) , k=1,2,3...nk=1,2,3...n
我们将其归纳成一般式子: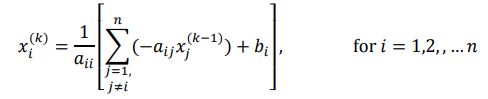
eg: 对于方程组: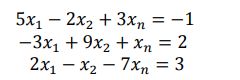
求解:
我们先将其变形: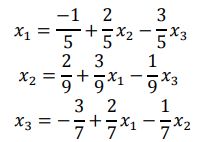
然后,我们假设:![]()
并将其代入得到: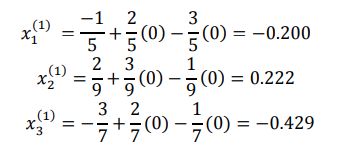
我们将得到的X1,x2,x3再次代入方程中,反复迭代,将会得到如下:
最终我们将会得到一个收敛值,该组值,就是我们得到的解(会非常的逼近真实解)
那么这种方法,也可以用来求解矩阵:
对于方程: Ax =b ; 我们设定 A矩阵为:  ,b矩阵为:
,b矩阵为: 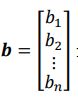 , x矩阵为:
, x矩阵为: 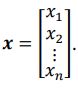
到这里,每个人都有自己的解法,直接的解法是将 x = A−1A−1b,但是A的逆矩阵A−1A−1,计算较为复杂,我们这里需要一点小的tricks ,我们将A矩阵拆分成为一个对角矩阵D,下三角矩阵L,上三角矩阵U,即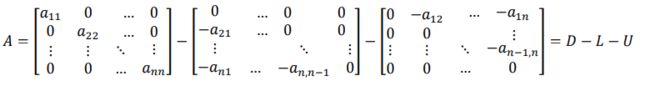
这样的话,公式 Ax = b 就变成了 ( D - L -U )x = b ,然后我们就可以得到:
Dx = b + (L+U)x ,当我们得到这个公式的时候,求解D的逆矩阵就容易了很多,我们得到D的逆矩阵为: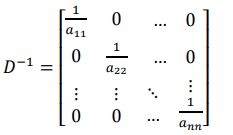
这个公式,和我们上面描述的雅克比迭代是不是长得很像,然后我们可以将其一般化为: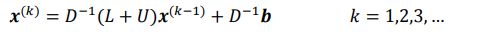
我们知道A是一个已知的常量矩阵,因而D,L,U都是已知矩阵,那么我们可以简化为:
T=D−1∗(L+U)T=D−1∗(L+U) , c=D−1∗bc=D−1∗b ;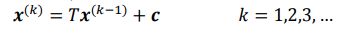
实现代码为:
参考资料为:
https://www3.nd.edu/~zxu2/acms40390F12/Lec-7.3.pdf