自然语言处理之LDA主题模型
1. LDA基本原理
1.1 PLSA
Hoffman 于 1999 年提出的PLSA,Hoffman 认为一篇文档(Document) 可以由多个主题(Topic) 混合而成, 而每个Topic 都是词汇上的概率分布,文章中的每个词都是由一个固定的 Topic 生成的。
文档和文档之间是独立可交换的,同一个文档内的词也是独立可交换的,这是一个 bag-of-words 模型。 存在K个topic-word的分布,我们可以记为 ϕ 1 , … , ϕ K \phi_1,\dots,\phi_K ϕ1,…,ϕK,对于包含M篇文档的语料 C = ( d 1 , d 2 , … , d M ) C=(d_1,d_2,\dots,d_M) C=(d1,d2,…,dM)中的每篇文档 d m d_m dm,都会有一个特定的doc-topic分布 θ m \theta_m θm。于是在 PLSA 这个模型中,第m篇文档 d m d_m dm 中的每个词的生成概率为
p ( w ∣ d m ) = ∑ z = 1 K p ( w ∣ z ) p ( z ∣ d m ) = ∑ z = 1 K ϕ z w θ m z p(w|d_m) = \sum \limits _{z=1}^K p(w|z)p(z|d_m)=\sum \limits _{z=1}^{K}\phi_{zw}\theta_{mz} p(w∣dm)=z=1∑Kp(w∣z)p(z∣dm)=z=1∑Kϕzwθmz
所以整篇文档的生成概率为
p ( w ⃗ ∣ d m ) = ∏ i = 1 n ∑ z = 1 K p ( w i ∣ z ) p ( z ∣ d m ) = ∏ i = 1 n ∑ z = 1 K ϕ z w i θ m z p(w⃗ |dm)=\prod \limits _{i=1}^{n} \sum \limits _{z=1}^{K}p(w_i|z)p(z|d_m)=\prod \limits _{i=1}^{n}\sum_{z=1}^{K}\phi_{z_{wi}}\theta_{mz} p(w⃗∣dm)=i=1∏nz=1∑Kp(wi∣z)p(z∣dm)=i=1∏nz=1∑Kϕzwiθmz
由于文档之间相互独立,我们也容易写出整个语料的生成概率。求解PLSA 这个 Topic Model 的过程汇总,模型参数并容易求解,可以使用著名的 EM 算法进行求得局部最优解。
1.2 LDA
LDA(隐含狄利克雷分配模型)主题模型是一族生成式有向图模型,主要用于处理离散的数据(如文本集合),在信息检索、自然语言处理等领域有广泛应用。(LDA)是主题模型的典型代表。
主题模型中的概念:词(word)、文档(document)、主题(topic)。
任务:拿到一个文本集合并对它做反向工程,从中发现都有哪些主题,以及每个文档属于哪个主题。
假设数据集中一共包含K个话题和M篇文档,文档中的词来自一个包含N个词的词典。我们用M个N维向量W表示数据集(文档集合),用K个N维向量 ϕ \phi ϕ表示话题。 LDA从生成模型的角度来看待文档和话题,LDA认为每篇文档包含多个话题,用 θ m \theta_m θm(K维)表示文档m中所包含的每个话题的比例, θ m , k \theta_{m,k} θm,k即表示文档m中包含话题k的比例,进而通过下面步骤生成文档m:
根据参数为αα的狄利克雷分布随机采样一个话题分布θmθm (较大的αα会导致每个文档中包含更多的主题)
按如下步骤生成文档中的N个词:
根据 θ m \theta_m θm进行话题指派,得到文档t中词n的话题 z m , n z_{m,n} zm,n
根据指派的话题所对应的词频分布 ϕ k \phi_{k} ϕk随机采样生成词 w m , n w_{m,n} wm,n
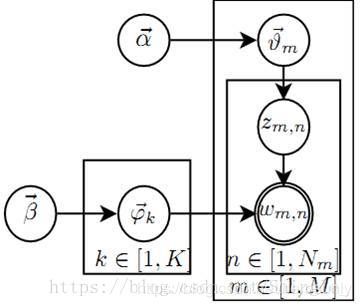
α \alpha α is the parameter of the Dirichlet prior on the per-document topic distributions,
β \beta β is the parameter of the Dirichlet prior on the per-topic word distribution,
θ m \theta_m θm is the topic distribution for document m,
ϕ k \phi_k ϕkis the word distribution for topic k,
z m n z_{mn} zmn is the topic for the n-th word in document m,
w m n w_{mn} wmn is the specific word.
上述只有词 w i j w_{ij} wij是观测变量,其他变量都是隐含变量。
显然,这样生成的文档自然地以不同比例包含多个主题,文档中的每个词来自一个主题,而这个主题是依据主题比例产生的。
LDA模型对应的概率分布为:
p ( W , z , ϕ , θ ∣ α , β ) = ∏ m = 1 M p ( θ m ∣ α ) ∏ i = 1 K p ( ϕ k ∣ β ) ( ∏ n = 1 N P ( w m , n ∣ z m , n , ϕ k ) P ( z m , n ∣ θ m ) ) p(W,z,\phi,\theta|\alpha,\beta)=\prod \limits_{m=1}^{M}p(\theta_m|\alpha) \prod \limits _{i=1}^{K}p(\phi_k|\beta)(\prod \limits _{n=1}^{N}P(w_{m,n}|z_{m,n},\phi_k)P(z_m,n|\theta_m)) p(W,z,ϕ,θ∣α,β)=m=1∏Mp(θm∣α)i=1∏Kp(ϕk∣β)(n=1∏NP(wm,n∣zm,n,ϕk)P(zm,n∣θm))
若模型已知,即参数 α \alpha α和 β \beta β已确定,则根据词频 w m , n w_{m,n} wm,n来推断文档集所对应的话题结构(即推断 ϕ k \phi_{k} ϕk, θ m \theta_{m} θm 和 z m , n z_{m,n} zm,n则可以通过求解:
p ( z , ϕ , θ ∣ W , α , β ) = p ( W , z , ϕ , θ ∣ α , β ) P ( W ∣ α , β ) p(z,\phi,\theta|W,\alpha,\beta)= \frac{p(W,z,ϕ,θ|α,β)}{P(W|α,β)} p(z,ϕ,θ∣W,α,β)=P(W∣α,β)p(W,z,ϕ,θ∣α,β)
然而分母上的P(W|α,β)P(W|α,β)难以获取,上式难以直接求解,因此实践中通过采样吉布斯采样或变分法进行近似推断。
model = models.LdaModel(corpus, id2word=dictionary, num_topics=100)
LDA可以视为PLSA的经验贝叶斯版本,由于PLSA不是指数族分布,而是其混合分布,因此其贝叶斯版本不能使用EM算法。
- Deterministic inference:可用变分近似,假设z和θθ的后验分布独立迭代求解过程与EM非常相似,称为VBEM;在大多数问题上无法保证收敛到局部最优。
- Probabilistic inference:可用Gibbs-sampling(Markov-chain Monte-Carlo, MCMC, 的一种),以概率1收敛到局部最优。
2. LDA优缺点
LDA算法既可以用来降维,又可以用来分类,但是目前来说,主要还是用于降维。
LDA算法的主要优点有:
-
在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
-
LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
LDA算法的主要缺点有:
-
LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
-
LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
-
LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好。
-
LDA可能过度拟合数据。
3.LDA参数学习
sklearn中LatentDirichletAllocation类的主要输入参数:
-
n_topics: 即我们的隐含主题数K,需要调参。K的大小取决于我们对主题划分的需求,比如我们只需要类似区分是动物,植物,还是非生物这样的粗粒度需求,那么K值可以取的很小,个位数即可。如果我们的目标是类似区分不同的动物以及不同的植物,不同的非生物这样的细粒度需求,则K值需要取的很大,比如上千上万。此时要求我们的训练文档数量要非常的多。
-
doc_topic_prior:即我们的文档主题先验Dirichlet分布θd的参数α。一般如果我们没有主题分布的先验知识,可以使用默认值1/K。
-
topic_word_prior:即我们的主题词先验Dirichlet分布βk的参数η。一般如果我们没有主题分布的先验知识,可以使用默认值1/K。
-
learning_method: 即LDA的求解算法。有 ‘batch’ 和 ‘online’两种选择。 ‘batch’即我们在原理篇讲的变分推断EM算法,而"online"即在线变分推断EM算法,在"batch"的基础上引入了分步训练,将训练样本分批,逐步一批批的用样本更新主题词分布的算法。默认是"online"。选择了‘online’则我们可以在训练时使用partial_fit函数分布训练。不过在scikit-learn 0.20版本中默认算法会改回到"batch"。建议样本量不大只是用来学习的话用"batch"比较好,这样可以少很多参数要调。而样本太多太大的话,"online"则是首先了。
-
learning_decay:仅仅在算法使用"online"时有意义,取值最好在(0.5, 1.0],以保证"online"算法渐进的收敛。主要控制"online"算法的学习率,默认是0.7。一般不用修改这个参数。
-
learning_offset:仅仅在算法使用"online"时有意义,取值要大于1。用来减小前面训练样本批次对最终模型的影响。
-
max_iter :EM算法的最大迭代次数。
-
total_samples:仅仅在算法使用"online"时有意义, 即分步训练时每一批文档样本的数量。在使用partial_fit函数时需要。
-
batch_size: 仅仅在算法使用"online"时有意义, 即每次EM算法迭代时使用的文档样本的数量。
-
mean_change_tol :即E步更新变分参数的阈值,所有变分参数更新小于阈值则E步结束,转入M步。一般不用修改默认值。
-
max_doc_update_iter: 即E步更新变分参数的最大迭代次数,如果E步迭代次数达到阈值,则转入M步。
从上面可以看出,如果learning_method使用"batch"算法,则需要注意的参数较少,则如果使用"online",则需要注意"learning_decay", “learning_offset”,“total_samples”和“batch_size”等参数。无论是"batch"还是"online", n_topics(K), doc_topic_prior(α), topic_word_prior(η)都要注意。如果没有先验知识,则主要关注与主题数K。可以说,主题数K是LDA主题模型最重要的超参数。
4. 之前特征+LDA特征 完成文本分类
4.1 读取数据
from sklearn.datasets import fetch_20newsgroups
import numpy as np
import pandas as pd
#初次使用这个数据集的时候,会在实例化的时候开始下载
data = fetch_20newsgroups()
categories = ["sci.space" #科学技术 - 太空
,"rec.sport.hockey" #运动 - 曲棍球
,"talk.politics.guns" #政治 - 枪支问题
,"talk.politics.mideast"] #政治 - 中东问题
train = fetch_20newsgroups(subset="train",categories = categories)
test = fetch_20newsgroups(subset="test",categories = categories)
4.2 使用TF-IDF将文本数据编码
from sklearn.feature_extraction.text import TfidfVectorizer as TFIDF
Xtrain = train.data
Xtest = test.data
Ytrain = train.target
Ytest = test.target
tfidf = TFIDF().fit(Xtrain)
Xtrain_ = tfidf.transform(Xtrain)
Xtest_ = tfidf.transform(Xtest)
Xtrain_
tosee = pd.DataFrame(Xtrain_.toarray(),columns=tfidf.get_feature_names())
tosee.head()
tosee.shape
4.3 LDA特征 完成文本分类
from sklearn.decomposition import LatentDirichletAllocation
clf = LatentDirichletAllocation(n_topics=14,
max_iter=50,
learning_method='batch')
clf.fit(Xtrain_ , Ytrain)
score = clf.score(Xtest_,Ytest)
print("\tAccuracy:{:.3f}".format(score))