感知机原理与python实现
感知机原理与python实例
原理
线性可分
给定一个二类数据集的标签为正负1,如果存在某个超平面 S S S:
w x + b = 0 wx + b = 0 wx+b=0
将所有正负实例点完全正确地划分到超平面的两侧,即对 y = + 1 y = +1 y=+1的实例有: w x + b > 0 wx + b > 0 wx+b>0;即对 y = − 1 y = -1 y=−1的实例有: w x + b < 0 wx + b < 0 wx+b<0.
判别函数
针对标签为正负1的二分类问题,感知机的判别函数为:
f ( x ) = s i g n ( w x + b ) f(x) = sign(wx + b) f(x)=sign(wx+b)
损失函数
自然地想,损失函数应当是误分类的点的个数,但是这个函数是不可导的,所以优化起来比较困难。
考虑 R n R^n Rn空间中的任意一点 x 0 x_0 x0到超平面的距离为:
1 ∣ ∣ w ∣ ∣ 2 ( w x 0 + b ) \frac{1}{||w||_2}(wx_0 + b) ∣∣w∣∣21(wx0+b)
对应误分类集合 M M M中的点来说:
− y ∣ ∣ w ∣ ∣ 2 ( w x + b ) > 0 -\frac{y}{||w||_2}(wx + b) > 0 −∣∣w∣∣2y(wx+b)>0
所以最终选择的损失函数为:
L ( w , b ) = − ∑ x ∈ M y ( w x + b ) L(w, b) = -\sum_{x \in M}y(wx + b) L(w,b)=−x∈M∑y(wx+b)
学习过程
目前学习的过程就变成使损失函数最小化的过程。
( w , b ) = arg min w , b L ( w , b ) ∂ L ∂ w = − ∑ x ∈ M y x ∂ L ∂ b = − ∑ x ∈ M y \begin{aligned} (w, b) &= \arg \min_{w, b}L(w, b) \\ \frac{\partial L}{\partial w} &= -\sum_{x \in M}yx \\ \frac{\partial L}{\partial b} &= -\sum_{x \in M}y \end{aligned} (w,b)∂w∂L∂b∂L=argw,bminL(w,b)=−x∈M∑yx=−x∈M∑y
通过梯度下降的方式,在每次迭代过程中以学习率 η \eta η更新 w , b w, b w,b的值,直到结果收敛或者达到指定的迭代次数为止。
w t = w t − 1 − η ∂ L ∂ w b t = b t − 1 − η ∂ L ∂ b w^t = w^{t - 1} - \eta\frac{\partial L}{\partial w} \\ b^t = b^{t - 1} - \eta\frac{\partial L}{\partial b} \\ wt=wt−1−η∂w∂Lbt=bt−1−η∂b∂L
收敛性证明
下面证明当数据是线性可分的情况下,感知机准则是一定收敛的。通过两种方法来进行证明。
方式一
方便起见,令 a = ( w T , b ) T , z = ( x T , 1 ) T a = (w^T, b)^T, z = (x^T, 1)^T a=(wT,b)T,z=(xT,1)T。
设最优的权重解为: a ^ \hat{a} a^,一定满足 ∀ x i , a ^ T z y i > 0 \forall x_i, \hat{a}^Tzy_i > 0 ∀xi,a^Tzyi>0。
假设经过 t t t轮迭代之后的解为: a t a^t at,在这一轮中仍然被分错的向量集合为: E ( t ) = { z ∣ a T z y < 0 } E(t) = \lbrace z|a^Tzy < 0 \rbrace E(t)={z∣aTzy<0},根据上文描述的梯度下降的规则,在第 t + 1 t + 1 t+1轮中,权重应当被更新为:
a ( t + 1 ) = a t + ∑ x i ∈ E ( t ) y i z i a^{(t + 1)} = a^t + \sum_{x_i \in E(t)}y_iz_i a(t+1)=at+xi∈E(t)∑yizi
令
∑ x i ∈ E ( t ) y i a t T z i = e ( t ) < 0 \sum_{x_i \in E(t)}y_i{a^t}^Tz_i = e(t) < 0 xi∈E(t)∑yiatTzi=e(t)<0
Proof:
∣ ∣ a ( t + 1 ) − α a ^ ∣ ∣ 2 = ∣ ∣ a t + ∑ x i ∈ E ( t ) y i z i − α a ^ ∣ ∣ 2 = ∣ ∣ a t − α a ^ ∣ ∣ 2 + 2 ( a t − α a ^ ) T ∑ x i ∈ E ( t ) y i z i + ∣ ∣ ∑ x i ∈ E ( t ) y i z i ∣ ∣ 2 = ∣ ∣ a t − α a ^ ∣ ∣ 2 + 2 e ( t ) − 2 α a ^ T ∑ x i ∈ E ( t ) y i z i + ∣ ∣ ∑ x i ∈ E ( t ) y i z i ∣ ∣ 2 ≤ ∣ ∣ a t − α a ^ ∣ ∣ 2 − 2 α a ^ T ∑ x i ∈ E ( t ) y i z i + ∣ ∣ ∑ x i ∈ E ( t ) y i z i ∣ ∣ 2 ( ⋆ ) D = ∑ x i ∈ E ( t ) ∣ ∣ y i z i ∣ ∣ ≥ ∑ x i ∈ E ( t ) ∣ ∣ y i z i ∣ ∣ ≥ ∣ ∣ ∑ x i ∈ E ( t ) y i z i ∣ ∣ ρ = min i y i a ^ T z i l e t α = D 2 ρ ( ⋆ ) ≤ ∣ ∣ a t − α a ^ ∣ ∣ 2 − 2 α ρ + D 2 = ∣ ∣ a t − α a ^ ∣ ∣ 2 − D 2 ≤ ∣ ∣ a 0 − α a ^ ∣ ∣ 2 − ( t + 1 ) D 2 s o ∃ t ^ s . t . a t ^ = α a ^ \begin{aligned} ||a^{(t + 1)} - \alpha \hat{a}||^2 &= ||a^t + \sum_{x_i \in E(t)}y_iz_i - \alpha \hat{a}||^2 \\ &= ||a^t - \alpha \hat{a}||^2 + 2(a^t - \alpha \hat{a})^T\sum_{x_i \in E(t)}y_iz_i + ||\sum_{x_i \in E(t)}y_iz_i||^2 \\ &=||a^t - \alpha \hat{a}||^2 + 2e(t) - 2\alpha\hat{a}^T\sum_{x_i \in E(t)}y_iz_i + ||\sum_{x_i \in E(t)}y_iz_i||^2 \\ &\le ||a^t - \alpha \hat{a}||^2 - 2\alpha\hat{a}^T\sum_{x_i \in E(t)}y_iz_i + ||\sum_{x_i \in E(t)}y_iz_i||^2 \qquad(\star)\\ D &= \sum_{x_i \in E(t)}||y_iz_i|| \ge \sum_{x_i \in E(t)}||y_iz_i|| \ge||\sum_{x_i \in E(t)}y_iz_i|| \\ \rho &=\min_i y_i\hat{a}^Tz_i \\ let \qquad \alpha &= \frac{D^2} {\rho} \\ (\star) &\le ||a^t - \alpha \hat{a}||^2 - 2\alpha\rho + D^2 \\ &= ||a^t - \alpha \hat{a}||^2 - D^2 \\ &\le ||a^0 - \alpha \hat{a}||^2 - (t + 1)D^2 \\ so \qquad \exists \hat{t} \quad s.t. \space a^{\hat{t}} &= \alpha \hat{a} \end{aligned} ∣∣a(t+1)−αa^∣∣2Dρletα(⋆)so∃t^s.t. at^=∣∣at+xi∈E(t)∑yizi−αa^∣∣2=∣∣at−αa^∣∣2+2(at−αa^)Txi∈E(t)∑yizi+∣∣xi∈E(t)∑yizi∣∣2=∣∣at−αa^∣∣2+2e(t)−2αa^Txi∈E(t)∑yizi+∣∣xi∈E(t)∑yizi∣∣2≤∣∣at−αa^∣∣2−2αa^Txi∈E(t)∑yizi+∣∣xi∈E(t)∑yizi∣∣2(⋆)=xi∈E(t)∑∣∣yizi∣∣≥xi∈E(t)∑∣∣yizi∣∣≥∣∣xi∈E(t)∑yizi∣∣=iminyia^Tzi=ρD2≤∣∣at−αa^∣∣2−2αρ+D2=∣∣at−αa^∣∣2−D2≤∣∣a0−αa^∣∣2−(t+1)D2=αa^
收敛性证毕。
方式二(Novikoff定理)
设训练集 T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T = \lbrace (x_1, y_1), ..., (x_N, y_N) \rbrace T={(x1,y1),...,(xN,yN)}是线性可分的,设 y i ∈ { + 1 , − 1 } , i = 1 , 2 , . . . , N y_i \in \lbrace +1, -1 \rbrace, i = 1, 2, ..., N yi∈{+1,−1},i=1,2,...,N,则
- 存在满足条件 ∣ ∣ w o p t ^ = 1 ∣ ∣ ||\hat{w_{opt}} = 1|| ∣∣wopt^=1∣∣的超平面 w o p t ^ ⋅ x ^ = w o p t ⋅ x + b o p t \hat{w_{opt}} \cdot \hat{x} = w_{opt} \cdot x + b_{opt} wopt^⋅x^=wopt⋅x+bopt将训练集完全分开;且存在 γ > 0 \gamma > 0 γ>0满足:
y i ( w o p t ^ ⋅ x ^ ) ≥ γ , ∀ i y_i(\hat{w_{opt}} \cdot \hat{x}) \ge \gamma, \qquad \forall i yi(wopt^⋅x^)≥γ,∀i - 令 R = max 1 ≤ i ≤ N ∣ ∣ x i ^ ∣ ∣ R = \max_{1 \le i \le N}||\hat{x_i}|| R=max1≤i≤N∣∣xi^∣∣,则感知机算法在训练数据机上的误分类次数 k k k满足不等式:
k ≤ ( R γ ) 2 k \le (\frac{R}{\gamma})^2 k≤(γR)2
Proof:
- 因为线性可分,所以:
y i ( w o p t ^ ⋅ x ^ ) > 0 y_i(\hat{w_{opt}} \cdot \hat{x}) > 0 yi(wopt^⋅x^)>0
令
γ = min i y i ( w o p t ^ ⋅ x ^ ) \gamma = \min_iy_i(\hat{w_{opt}} \cdot \hat{x}) γ=iminyi(wopt^⋅x^)
即可 - 由梯度下降的权值更新方式可知:
w k ^ = w ^ k − 1 + η y i x i \hat{w_k} = \hat{w}_{k - 1} + \eta y_ix_i wk^=w^k−1+ηyixi
在这里我们每出现一个误分类的数据就进行一次权值更新, w k w_k wk指出现第 k k k个误分类的错误时候更新得到的权重,假定初始权重 w 0 w_0 w0为 0 0 0.
则有
w k ^ ⋅ w ^ o p t ≥ w ^ k − 1 ⋅ w ^ o p t + η γ ≥ w ^ k − 2 ⋅ w ^ o p t + 2 η γ ⋯ ≥ w ^ 0 ⋅ w ^ o p t + k η γ = k η γ ( 1 ) \begin{aligned} \hat{w_k} \cdot \hat{w}_{opt} &\ge \hat{w}_{k - 1} \cdot \hat{w}_{opt} + \eta\gamma \\ &\ge \hat{w}_{k - 2} \cdot \hat{w}_{opt} + 2\eta\gamma \\ &\cdots \\ &\ge \hat{w}_{0} \cdot \hat{w}_{opt} + k\eta\gamma \\ & = k\eta\gamma \qquad (1) \end{aligned} wk^⋅w^opt≥w^k−1⋅w^opt+ηγ≥w^k−2⋅w^opt+2ηγ⋯≥w^0⋅w^opt+kηγ=kηγ(1)
另有
∣ ∣ w k ^ ∣ ∣ 2 = ∣ ∣ w ^ k − 1 + η y i x i ∣ ∣ 2 = ∣ ∣ w ^ k − 1 ∣ ∣ 2 + 2 η y i w ^ k − 1 T x i + ∣ ∣ η y i x i ∣ ∣ 2 ≤ ∣ ∣ w ^ k − 1 ∣ ∣ 2 + η 2 R 2 ⋯ ≤ ∣ ∣ w ^ 0 ∣ ∣ 2 + k η 2 R 2 = k η 2 R 2 ( 2 ) \begin{aligned} ||\hat{w_k}||^2 &= ||\hat{w}_{k - 1} + \eta y_ix_i||^2 \\ &= ||\hat{w}_{k - 1}||^2 + 2\eta y_i{\hat{w}_{k - 1}}^Tx_i + ||\eta y_ix_i||^2 \\ & \le ||\hat{w}_{k - 1}||^2 + \eta^2R^2 \\ &\cdots \\ &\le ||\hat{w}_{0}||^2 + k\eta^2R^2 \\ &= k\eta^2R^2 \qquad (2) \end{aligned} ∣∣wk^∣∣2=∣∣w^k−1+ηyixi∣∣2=∣∣w^k−1∣∣2+2ηyiw^k−1Txi+∣∣ηyixi∣∣2≤∣∣w^k−1∣∣2+η2R2⋯≤∣∣w^0∣∣2+kη2R2=kη2R2(2)
结合 ( 1 ) ( 2 ) (1)(2) (1)(2)得到:
k η γ ≤ w k ^ ⋅ w ^ o p t ≤ ∣ ∣ w k ^ ∣ ∣ ⋅ ∣ ∣ w ^ o p t ∣ ∣ ≤ k η R k ≤ ( R γ ) 2 \begin{aligned} k\eta\gamma \le \hat{w_k} \cdot \hat{w}_{opt} &\le ||\hat{w_k}|| \cdot ||\hat{w}_{opt}|| \le \sqrt{k}\eta R \\ k &\le {(\frac{R}{\gamma})}^2 \end{aligned} kηγ≤wk^⋅w^optk≤∣∣wk^∣∣⋅∣∣w^opt∣∣≤kηR≤(γR)2
故感知机一定在有限步内收敛。
对偶形式
感知机的对偶形式为
f ( x ) = s i g n ( ∑ j = 1 N α j y j x j ⋅ x + ∑ i = 1 N α i y i ) f(x) = sign(\sum_{j = 1}^{N}\alpha_jy_jx_j \cdot x + \sum_{i = 1}^{N}\alpha_iy_i) f(x)=sign(j=1∑Nαjyjxj⋅x+i=1∑Nαiyi)
可以发现只是权值的变化了一种形式,这一点可以直接从梯度下降的递推公式中看出来。(默认初始权值都是1)。需要说明的是 α i \alpha_i αi表示的是第 i i i个数据在整个过程中被分错的次数。
对应的学习过程也就变成了改变 α \alpha α的过程,每当出现一个数据被分错了,就 α i = α i + η \alpha_i = \alpha_i + \eta αi=αi+η直到收敛为止。
另外还有一点就是整个训练的过程对于数据本身仅以内积的形式出现,可以预先计算好内积的矩阵,即Gram矩阵:
G = [ x i ⋅ x j ] N × N G = \lbrack x_i \cdot x_j \rbrack_{N \times N} G=[xi⋅xj]N×N
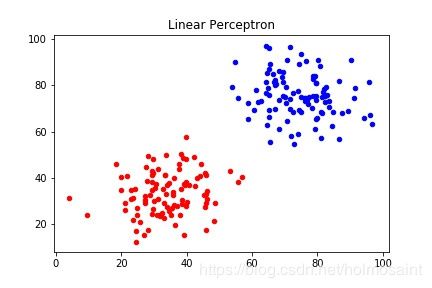
实例
然后将数据转化为numpy中的array形式,并且设置标签为 { − 1 , + 1 } \lbrace -1, +1\rbrace {−1,+1},初始化权重都是 0 0 0.
data = np.vstack([data0, data1])
label = np.hstack([np.ones(data0.shape[0]) * -1.0, np.ones(data1.shape[0])]).reshape(len(data), 1)
data = np.c_[data, np.ones(len(data))]
随后是算法的主体——梯度下降。在梯度下降的过程中,碰到的最大的困难就是梯度过大,导致整个算法不停的抖动,在这里很简单地降低学习率,其实应用随即梯度下降等优化算法可能会更好一些。
w = np.array([0.0, 0.0, 0.0]).reshape(1, 3)
error = 1
epoch = 0
learning_rate = 0.000001
while error != 0.0:
res = np.multiply(np.dot(w, data.T), label.T)[0]
print(res)
error = 0
epoch = epoch + 1
for i in range(len(res)):
x = -data[i] * label[i]
if res[i] <= 1e-3:
w = w - learning_rate * x
error = error + 1
print("Error rate in epoch {} is {:.2f}%".format(epoch, error / len(data) * 100))
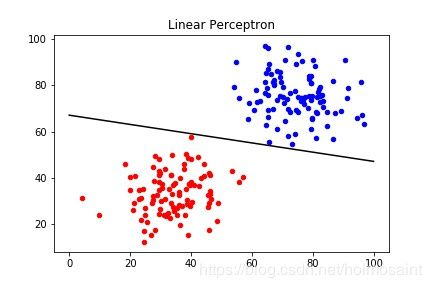
总共迭代了2651轮才最终收敛,最终的权值情况为:
[ 0.00027111 0.00135846 -0.091094 ]
参考资料
[1] 李航 《统计学习方法》 第2章