Aka_Happy

Python 信息熵条件信息熵互信息（信息增益）的理解以及计算代码

好久没更新博客了，最近在学习python的贝叶斯网络构造，卡在k2算法给无向图打分这一步很久了，然后微微头疼，决定把之前构造无向图里的自己写的小功能函数放出来，记录一下自己的成长过程，我比较菜，写出来如果有错误希望有缘人看到能够给出指正，如果没有错误，希望给路过的有缘人一些帮助！

文章知识大部分摘自通俗理解条件熵

（代码为原创，转载请标明！）

1 信息熵以及引出条件熵

1.1 信息熵

信息熵可以表示一个变量的不确定性

我们首先知道信息熵是考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。公式如下：

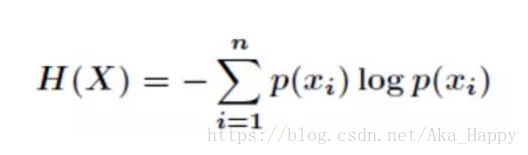
1.2 条件熵

条件熵定义为X给定条件下，Y的条件概率分布的熵对X的数学期望

这个还是比较抽象，下面我们解释一下：

设有随机变量（X,Y），其 联合概率 分布为：

条件熵H（Y|X） 表示在已知随机变量X的条件下随机变量Y的不确定性。

随机变量X给定的条件下，随机变量Y的条件熵：H(Y|X)

2 公式

下面推导一下条件熵的公式：

3 注意

注意，这个条件熵，不是指在给定某个数（某个变量为某个值）的情况下，另一个变量的熵是多少，变量的不确定性是多少？而是期望！

因为条件熵中X也是一个变量，意思是在一个变量X的条件下（变量X的每个值都会取），另一个变量Y熵对X的期望。

4 例子 :

下面通过例子来解释一下：

假如我们有上面数据：

设随机变量Y={嫁，不嫁}

我们可以统计出，嫁的个数为6/12 = 1/2 → P(Y=嫁) = 1/2

不嫁的个数为6/12 = 1/2 → P(Y=不嫁) = 1/2

那么Y的熵，根据 信息熵的公式 （见1.1）来算，可以得到 H（Y） = -1/2log1/2 -1/2log1/2

为了引出 条件熵，我们现在还有一个变量X，代表长相是帅还是帅，当长相是不帅的时候，统计如下红色所示：

可以得出，当已知X= 不帅的条件下，满足条件的只有4个数据了 → 这四个数据中，不嫁的个数为1个，占1/4 → P(Y=不嫁|X=不帅) = 1/4

嫁的个数为3个，占3/4 → P(Y=嫁|X=不帅) = 3/4

那么此时的 H（Y|X = 不帅） = -1/4log1/4-3/4log3/4

p(X = 不帅) = 4/12 = 1/3

↓

同理我们可以得到：

当已知X = 帅的条件下，满足条件的有8个数据了，这八个数据中，不嫁的个数为5个，占5/8 → P(Y=不嫁|X=帅) = 5/8

嫁的个数为3个，占3/8 → P(Y=嫁|X=帅) =3/8

那么此时的 H（Y|X = 帅） = -5/8log5/8-3/8log3/8

p(X = 帅) = 8/12 = 2/3

↓

5 计算结果

有了上面的铺垫之后，我们终于可以计算我们的条件熵了，我们现在需要求：

H（Y|X = 长相）

也就是说，我们想要求出当已知长相的条件下的条件熵。

根据公式我们可以知道，长相可以取 X=帅 与 X=不帅 两种

条件熵H（Y|X）是另一个变量Y熵对X（条件）的期望。

公式为：

H（Y|X=长相） = p(X =帅)H（Y|X=帅）+ p(X =不帅)H（Y|X=不帅）

然后将上面已经求得的答案带入即可求出条件熵！

这里比较容易错误就是忽略了 X也是可以取多个值，然后对其求期望！！

6. 代码部分：

基础函数定义：


def findAllIndexInList(aim, List):
    '''
    找到一个元素aim在列表List里全部的位置  并将所有的索引值打包成列表并返回
    '''
  
    pos = 0 	#pos代表List里each = aim时候each的索引值
    index=[] 	#所有pos打包到index里
    for each in List:
        if each == aim:
            index.append(pos)
        pos += 1
    return index

#把一个列表List里索引在Index里的元素取出来，元素组成一个 newList列表
def CreateNewListByIndex(Index, List):
    newList = []
    List = list(List)
    Index = list(Index)
    for each in Index:
        newList.append(List[each])
    return newList

#对一个列表List里的某个元素aim求概率 p(X=aim): 即 aim在List有多少个重复值/List元素总个数
def Pi(aim, List):
    length = len(list(List))  #求List一共有多少个元素，包括重复值
    aimcount = (list(List)).count(aim)	 #求aim在List里有多少个一样的值
    pi = (float)(aimcount/length)
    return pi

求信息熵H(x) = - Σ p(x_i)*log p(x_i):

import numpy as np
import math

def entropy(data: list):   #输入的data 是 X 所有取值（重复值不去除）的列表

    data1 = np.unique(data)  
    # 找到列表里所有值（去除重复值）组成一个新的列表data1
    #这里没有numpy库的 可以用set函数把data变成一个集合，也可以去除重复值~
    
    resultEn = 0    #单个元素的熵H(X)保存在resultEn
    
    for each in data1:    #data1里保存的值不重复
        pi = Pi(each, data)    #求出data（data里的值可能重复）中每个 xi出现的概率
        resultEn -= pi * math.log(pi, 2)     #对不同xi的信息熵求和过程

    return resultEn

运行示例：

dataX = [1, 1, 2, 2]   
print('H(X)为:', entropy(dataX))

这里可以看到： X出现的情况有 x=1,x=1,x=2,x=2
即p(x=1) = 1/2 ; p(x=2)=1/2

	H(X) = - p(x=1)*log p(x=1) -  - p(x=2)*log p(x=2)
		= 1/2 + 1/2 = 1

求条件熵H(X|Y):


# conditionalEntropy 求条件熵 H(X|Y) = Σp(yi)*H(X|Y=yi)

def conditionalEntropy(dataX: list, dataY: list):
    #先对dataY处理：
    #YElementsKinds是所有原先dataY列表里不重复的元素组成的新列表：
    
    YElementsKinds = list(np.unique(dataY))
    
    resultConEn = 0  #最终条件熵H(X|Y)

    #在每个不同的yi = uniqueYEle 条件下:
    for uniqueYEle in YElementsKinds:
    
        YIndex = findAllIndexInList(uniqueYEle, dataY)   
        #找出dataY 里所有等于yi = uniqueYEl的索引值组成的列表
        
        dataX_Y = CreateNewListByIndex(YIndex, dataX)   #找到dataX里所有索引在YIndex里的值组成一个列表

        HX_uniqueYEle = entropy(dataX_Y)      #此时可以计算 HX_uniqueYEle =  H（X|Y=yi)
        pi = Pi(uniqueYEle, dataY)            #此时可以计算 pi = p(Y=yi)
        resultConEn +=  pi * HX_uniqueYEle       # 求和 H（X|Y）= Σ p(Y=yi)*H（X|Y=yi)
    return resultConEn      #返回条件熵 H（X|Y）