java 数据结构——java实现顺序表、单链表

 线性表示数据结构的一种，它是 n 个具有相同特性的 数据元素的有限序列。

顺序表

顺序表指的是用一组地址连续的存储单元存储线性表中的数据元素，称为线性表的顺序存储结构或者顺序映像。线性表采用顺序存储的方式存储就称之为顺序表。

一 . 顺序表的建立。

class TestSqlist{
	int usedSize;//当前有效的数据元素的个数。
	int[] elem;//用一组地址连续的存储空间来存储顺序表的数据元素。
	public TestSqlist(){
		this(10);
	}
	public TestSqlist(int size){
		elem = new int[size];
		usedSize = 0;
	}
}

二 . 判断顺序表是否为满。

public boolean isFull(){
	return this.usedSize == elem.length;
}

三 . 插入一个数据。

 

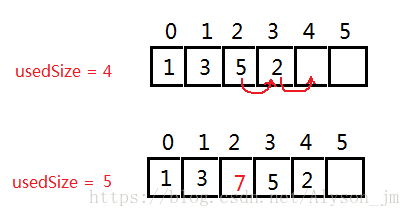
插入数据可以先将要插入的位置及后面的元素都向后移动一下，然后覆盖掉原来位置的元素。

 

public boolean insert(int pos,int val){
	//判断链表是否为满
	if(isFull()){
		elem = Arrays.copyOf(elem, elem.length*2);
		System.out.println(elem.length);
	}
	//判断pos合法性
	if(pos < 0 || pos > this.usedSize ){
		return false;
	}	
	for(int i = this.usedSize-1;i >= pos;i--){
		elem[i+1] = elem[i];
	}
	elem[pos] = val;
	this.usedSize++;
	return true;
}

四 . 判断顺序表是否为空。

public boolean isEmpty(){
	return this.usedSize == 0; 
}

五 . 删除一个数据。

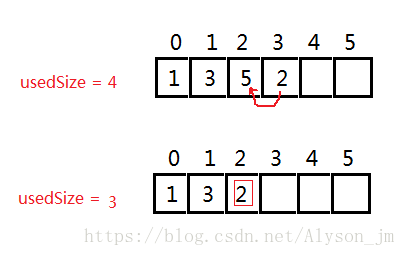
用要删除的元素的后面的元素覆盖掉要删除的元素即可。最后记得要使有效长度减 1 哦。

public boolean delete(int val){
	int i = search(val);
	//val不存在。
	if(i == -1){
		return false;
	}
	for(int j = i;j < this.usedSize-1;j++){
		elem[j] = elem[j+1];
	}
	this.usedSize--;
	return true;
}

六 . 查找一个元素。

从头开始遍历顺序表，如果找到这个元素，返回下标即可。

public int search(int key){
	//存在顺序表为空
	if(isEmpty()){
		return -1;
	}
	for(int i = 0;i < this.usedSize;i++){
		if(key == elem[i]){
			return i;
		}
	}
	return -1;
}

优点

• 无须为表示表中元素之间的逻辑关系而增加额外的存储空间
• 可以快速地存取表中任一位置的元素

缺点

• 插入和删除操作需要移动大量元素
• 当线性表长度变化较大时，难以确定存储空间的容量。
• 造成存储空间的碎片 

单链表

链式表示指的是用一组任意的存储单元存储线性表中的数据元素，线性表采用链式的存储方式称为链式表。

一 . 单链表的创建

class TestLink{
        class Entry{	//Entry Node
		int data;
		Entry next;//存储的是下一个节点的地址。
		public Entry(){
			data = -1;
			next = null;
		}
		public Entry(int val){
			data = val;
			next = null;
		}
	}	
	public Entry head;//指向头结点的引用
	public TestLink(){
		head = new Entry();
	}

二 . 头插法。

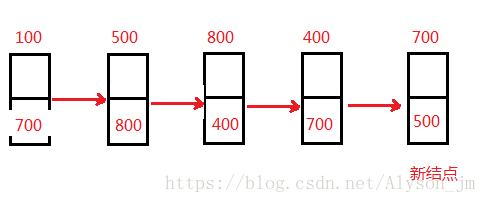
插入到头结点的后面，每次先将新结点的 next 域存储头结点的下一个地址，然后将头结点的 next 域存储新结点的地址。

public void insertHead(int val){
	Entry cur = new Entry(val);
	cur.next = head.next;
	head.next = cur;
}

 

三 . 尾插法。

 

遍历链表，直到遇到某个节点的 next域 为空，将新结点的地址存入即可。

public void insertTail(int val){
	Entry cur = new Entry(val);
	Entry t = head;
	while(t.next != null){
		t = t.next;
	}
	t.next = cur;
}

四 . 获取链表长度。

设置一个标志 len 来记录链表的长度，遍历节点，每次 len + 1。

public int getLenght(){
	int len = 0;
	Entry cur = head.next;
	while(cur != null){
		cur = cur.next;
	        len++;
	}
	return len;
}

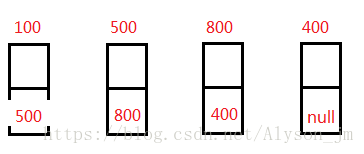
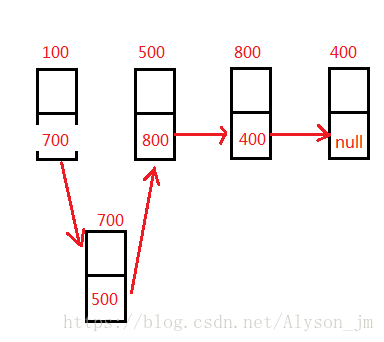
五 . 逆置数组。

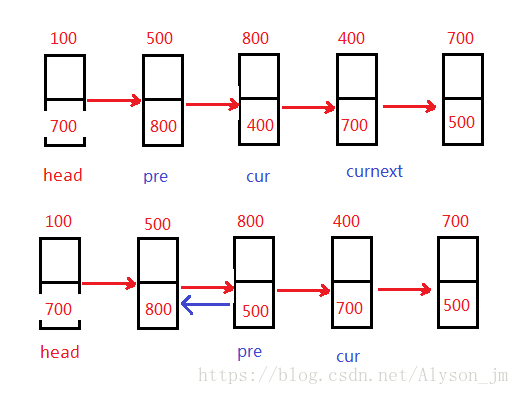
逆置其实就是将结点的 next 存储它们原来前驱结点的地址。下图是

public Entry reverse(){
        Entry pre = null;//前驱
	Entry cur = head;
	Entry newhead = head;
	while(cur != null){
		Entry curnext = cur.next;
		if(curnext == null){
			newhead = cur;
		}
		cur.next = pre;
		pre = cur;
		cur = curnext;
	}
	cur = newhead;
	while(cur.next != null){
		System.out.print(cur.data+"  ");
		cur = cur.next;
	}
	return newhead;
}

 

六 . 求倒数第 k 个节点。

 

 

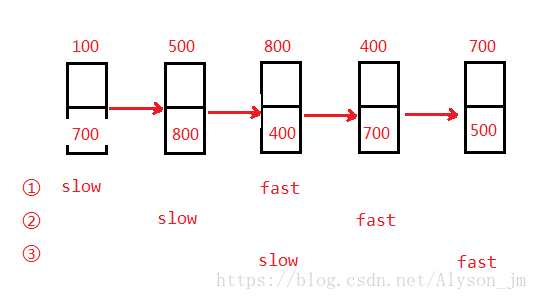
设置两个标志位，让fast先走k-1步，然后fast 和slow一块走，直到fast走到最后一个节点，此时slow就是倒数第k个节点。

public int lastK(int k){
	Entry fast = head;
	Entry slow = head;
	//判断参数的合法性
	if(k < 0 ||k > getLength()){
		return -1;
	}
	//fast 先走k-1步。
	while(k-1 > 0){
		fast = fast.next;
		k--;
	}
	//fast 和 slow 一起走，直到fast走到最后一个节点。
	while(fast.next != null){
		fast = fast.next;
		slow = slow.next;
	}
	return slow.data;
}

 

七 . 创造一个环。

//构造一个环
public void createLoop(){
	int len = getLength();
	Entry cur = head;
	while(cur.next != null){
		cur = cur.next;
	}
	cur.next = head.next.next;
}
	

 

七 . 判断单链表是否有环。

设置一个标志位，fast 和 slow，fast 每次走两步，slow 每次走一步，由数学归纳法得到，只要slow和fast相遇，就可以证明这是一个环。

public boolean isloop(){
	Entry slow = head.next;
	Entry fast = head.next;
	while(fast != null){
		fast = fast.next.next;
		slow = slow.next;
		if(fast == slow)//相遇点
			return true;
	}
	return false;
}

 

八 . 环的入口点。

 

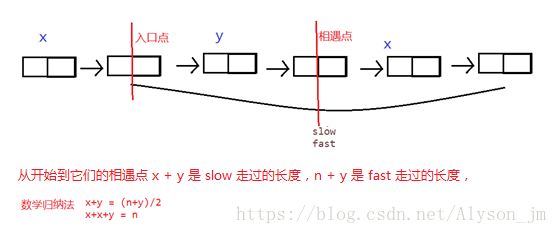
把slow放在头结点的位置，slow向前走x步，同时fast从相遇点开始也走x步，从图中可以看出，在入口点它们刚好相遇。

 

public int enterloop(){
	if(!isloop()){
		return -1;
	}
	Entry slow = head;
	Entry fast = head;
	while(fast != null){//快引用每次走两步，慢引用每次走一步。
		fast = fast.next.next;
		slow = slow.next;
		if(fast == slow)//相遇点
			break;
	}
	slow = head;//当两个引用再次相遇的时候就是在入口点。
	while(slow != fast){
		slow = slow.next;
		fast = fast.next;
	}
	return slow.data;
}

九 . 环的长度。

 

从图中看出环的长度为x+y， 同时从头结点到相遇点的距离也是环的x+y，所以使slow指向头结点，每次向后移动一位，同时len 加1。最后len就是环的长度。

public int getLengthLoop(){
	int len = 0;
	Entry slow = head;
	Entry fast = head;
	if(!isloop()){
		return -1;
	}
	while(fast != null){//快引用每次走两步，慢引用每次走一步。
		fast = fast.next.next;
		slow = slow.next;
		if(fast == slow)//相遇点
	        	break;
	}
	slow = head;
	while(slow != fast){
		slow = slow.next;
		len++;
	}
	return len;
}  

判断两个链表是否相交。

public static boolean isCut(TestLink1 l1,TestLink1 l2){
		TestLink1.Entry t1 = l1.getHead();
		TestLink1.Entry t2 = l2.getHead();
		int cha;
		if(l1.getLength() < l2.getLength()){
			//使 t1 始终指向比较长的链表。
			t1 = l2.getHead();
			t2 = l1.getHead();
			cha = l2.getLength() - l1.getLength();
		}else{
			cha = l1.getLength() - l2.getLength();
		}
		while(cha > 0){			
			t1 = t1.next;
			cha--;
		}
		while(t1 != t2 && t1!=null && t2!=null){
			t1 = t1.next;
			t2 = t2.next;
		}
		if(t1 == t2 && t1 !=null && t2 != null){
			System.out.println("交点："+t1.data);
			return true;
		}else{
			return false;
		}
	}

合并两个链表

public static TestLink1 merge(TestLink1 l1,TestLink1 l2){
		TestLink1.Entry newHead = null;
		TestLink1.Entry p1 = l1.getHead().next;
		TestLink1.Entry p2 = l2.getHead().next;
		TestLink1.Entry newtmpHead = null;
		if(p1.data < p2.data){
			newHead = l1.getHead();
		}else{
			newHead = l2.getHead();
		}
		newtmpHead = newHead;
		while(p1 != null && p2 != null){
			if(p1.data < p2.data){
				newtmpHead.next = p1;
				p1 = p1.next;
			}else if(p1.data > p2.data){
				newtmpHead.next = p2;
				p2 = p2.next;
			}else{
				newtmpHead.next = p1;
				p1 = p1.next;
				p2 = p2.next;
			}
			newtmpHead = newtmpHead.next;
		}
		if(p1 != null){
			newtmpHead.next = p1;
		}else{
			newtmpHead.next = p2;
		}
		return new TestLink1(newHead);
	}

单链表和顺序表的比较

存储分配方式

• 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素
• 单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素

时间性能

查找

• 顺序存储结构O（1）
• 链式存储结构O（n）

插入和删除

• 顺序存储结构需要平均移动表长一半的元素，时间为O（n）
• 单链表在找出某位置的指针后，插入和删除仅为O（1）

空间性能

• 顺序存储结构需要预分配存储空间，分大了浪费，分小了易发生上溢
• 单链表不需要分配存储空间，元素个数也不受限制