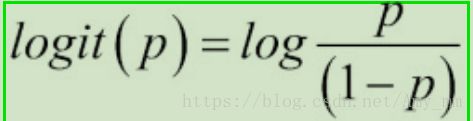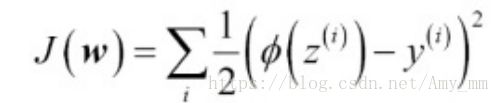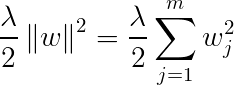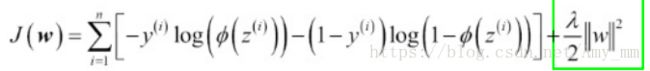逻辑回归模型（二）——sklearn实现逻辑回归（logistic regression）

【Modeling class probabilities via logistic regression】  

类概率的逻辑回归建模

， 

事件发生的几率（odds）定义为 事件发生概率与事件未发生概率的比值。logit函数代表事件的几率，其中p代表我们所预测事件发生的概率。

sigmoid 函数（S形函数）   ,   

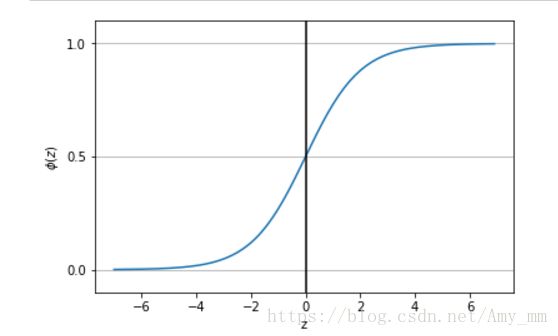
如下图sigmoid函数输入为全体实数，将输入转化为（0,1）之间的数

#sigmoid函数
import matplotlib.pyplot as plt
import numpy as np

def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))
z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)
plt.plot(z, phi_z)
plt.axvline(0.0,color = 'k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi(z)$')
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca() #Get Current Axes
ax.yaxis.grid(True)

【Learning the weights of the logistic cost function】

逻辑代价函数的权值

方差总和为    

似然函数(Likelyhood function)：

对数似然函数(log Likelyhood )：

对数似然函数进行最大化更简单~

代价函数（cost  function）:

可以采用剃度下降法对代价函数进行最小化优化。

为了更好的利用代价函数，先来看一下单个y的情况

可以看到如下特殊情况:

def cost_1(z):
    return - np.log(sigmoid(z))


def cost_0(z):
    return - np.log(1 - sigmoid(z))

z = np.arange(-10, 10, 0.1)
phi_z = sigmoid(z)

c1 = [cost_1(x) for x in z] 
plt.plot(phi_z, c1, label = 'J(w) if y = 1')

c0 = [cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle = '--', label = 'J(w) if y = 0')

plt.ylim(0.0, 5.1)
plt.xlim([0, 1])

plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc = 'best')
plt.tight_layout()
plt.show()

【将python实现的Adaline 接口转换为逻辑回归算法】

Adaline 地址：https://blog.csdn.net/Amy_mm/article/details/79668201

只需要改正3点：

（1） cost function： 平方误差——>对数似然函数

adaline   

logistic  

（2）激活函数改为sigmoid函数

adaline    

logistic  

（3）预测函数输出改为1,0

代码如下:

github源码地址：

 

class LogisticRegressionGD(object):
    """
    ADAptive LInear NEuron classifier.

    Parameters
    ------------
    eta : float #学习率
      Learning rate (between 0.0 and 1.0)
    n_iter : int  #迭代次数
      Passes over the training dataset.
    random_state : int  #随机数生成器参数
      Random number generator seed for random weight initialization.


    Attributes
    -----------
    w_ : 1d-array #权重
      Weights after fitting.
    cost_ : list #平方误差
      Sum-of-squares cost function value in each epoch.

    """
    # 参数初始化
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state
    # 拟合数据 进行权值更新 计算错误率
    
   
    def fit(self,X,y):
        '''
         """ Fit training data.

        Parameters
        ----------
        X : {array-like}, shape = [n_samples, n_features]
          Training vectors, where n_samples is the number of samples and
          n_features is the number of features.
          
        X：要进行拟合的输入数据集，有n_sample个样本，每个样本有n_feature个特征值
        例如 X = （[1,2,3],[4,5,6]） [1,2,3]为类别+1，[4,5,6]为类别-1
        
        y : array-like, shape = [n_samples]
          Target values.
        y:输出数据分类，{+1，-1}
        
        Returns
        -------
        self : object

        """
        '''
        rgen = np.random.RandomState(self.random_state)
        #将偏置b并入到w矩阵，所以大小为X行数加1       X.shape[1]代表行数，即样本个数
        self.w_ = rgen.normal(loc = 0.0, scale = 0.01, size = 1+ X.shape[1])
        self.cost_ = []
        
        for i in range(self.n_iter):
            #在这个代码中activation函数可以不用，写上它只是为了代码的通用性，
            #比如logistic代码中可以更改为sigmod函数
            net_input = self.net_input(X)
            output = self.activation(net_input)
            errors = (y - output)
            #更新原理见博客 https://mp.csdn.net/postedit/79668201
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()

            #代价函数改为逻辑回归的对数似然函数
            cost = - y.dot(np.log(output)) - ((1 - y).dot(np.log(1 - output)))
            #平方误差的总和 Sum of Squred Errors
            self.cost_.append(cost)
        return self
        
        # 净输入  X点乘W
    def net_input(self, X):
        return np.dot(X,self.w_[1:]) + self.w_[0]
        
        #在本代码中 activation没有意义  是为了以后logistic中可以用到
    def activation(self, z):
        return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
        
        #预测函数
    def predict(self, X):
        return np.where(self.net_input(X) >= 0.0, 1, 0 )
            

#logistic regression 只能用来进行二项分类
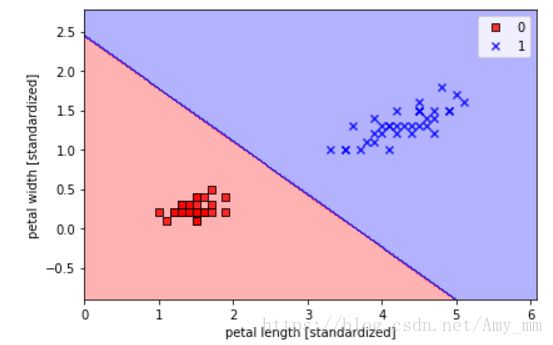
X_train_01_subset = X_train[(y_train == 0 )| (y_train == 1)]
y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]

lrgd = LogisticRegressionGD(eta = 0.05, n_iter = 1000, random_state = 1 )

lrgd.fit(X_train_01_subset, y_train_01_subset)

plot_decision_regions(X = X_train_01_subset, 
                      y = y_train_01_subset, 
                      classifier = lrgd)

plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc = 'best')
plt.tight_layout()
plt.show()
    
  

【Training a logistic regression model with scikit-learn】

利用sklearn库实现逻辑回归

从linear_model类中调用LogisticRegression模型

#sklearn实现逻辑回归 logistic regression
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C = 100.0, random_state = 1)
lr.fit(X_train_std, y_train)
plot_decision_regions(X = X_combined_std, 
                     y = y_combined, 
                     classifier = lr, 
                     test_idx = range(105,150) )
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
#plt.savefig('images/03_06.png', dpi=300)
plt.show()sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C = 100.0, random_state = 1)
lr.fit(X_train_std, y_train)
plot_decision_regions(X = X_combined_std, 
                     y = y_combined, 
                     classifier = lr, 
                     test_idx = range(105,150) )
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
#plt.savefig('images/03_06.png', dpi=300)
plt.show()

 

【predict_proba 】返回一个n行k列的数组，第i行第j列上的数值是模型预测第i个预测样本的标签为j的概率。所以每一行的和应该等于1.

lr.predict_proba(X_test_std[:3,:])

第一行表示测试集中的第一个数据分类为三种花类别的概率。以下同此。

【argmax】按轴向识别最大值

#argmax(axis = 1 / 0 )——> axis = 0为列向，axis = 1 为横向
lr.predict_proba(X_test_std[:3, :]).argmax(axis = 1)

识别每行的最大值，返回最大值的下标。其中，Iris-virginica ,ris-setosa , and Iris-setosa  分别为0,1,2。

【LR模型中的predict函数结合了二者，直接返回预测类型】

lr.predict(X_test_std[:3, :])

【overfitting and underfitting】

过拟合：模型参数太多，太复杂

拟合不够：模型太简单

正则化方法解决过拟合问题。正则化过滤掉信息中的杂乱信息，避免过拟合。正则化的数据必须是可比较的，所以数据必须进行标准化（standardized）以便利于之后的正则化处理。

L2正则化：     ,其中为正则化参数。

对于逻辑回归模型中的代价函数cost function 可以加入简单的正则化项，实现正则化，如下

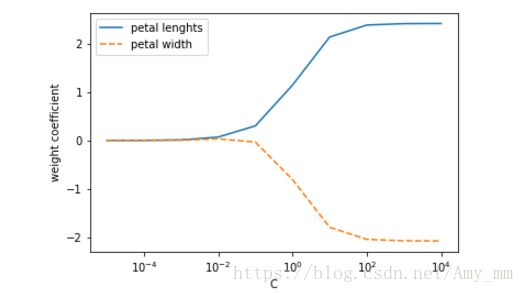
sklearn库中的LogisticRegression类中的参数C即正则化参数的倒数。用代码plot参数C与权值参数W的关系

from sklearn.linear_model import LogisticRegression
import  matplotlib.pyplot as plt 

weights, params = [], []
for c in np.arange(-5, 5):
    lr = LogisticRegression(C = 10.** c, random_state = 1)
    lr.fit(X_train_std,y_train)
    weights.append(lr.coef_[1])
    params.append(10.** c)
weights = np.array(weights)
plt.plot(params, weights[: , 0], 
         label = 'petal lenghts')

plt.plot(params, weights[: , 1], 
         linestyle = '--', 
         label = 'petal width')

plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.legend(loc='upper left')
plt.xscale('log')
#plt.savefig('images/03_08.png', dpi=300)
plt.show()

如图，如果减小C，也就是增强正则化，权重W呈缩减趋势。

下一篇博文继续学习sklearn库中SVM的实现。