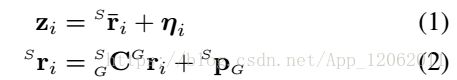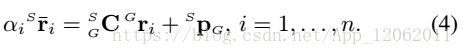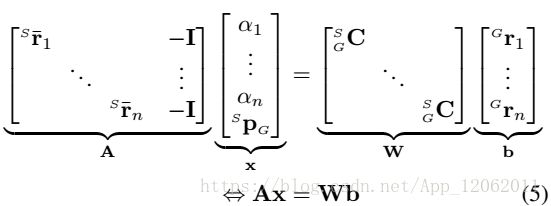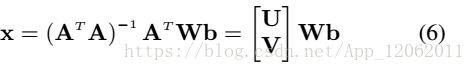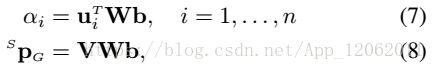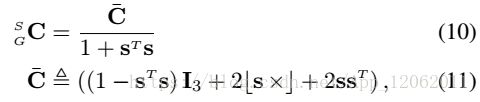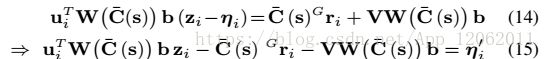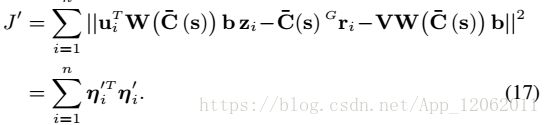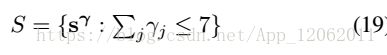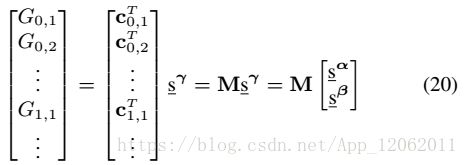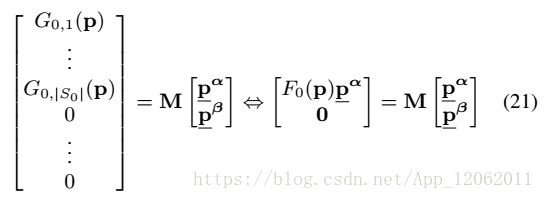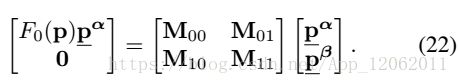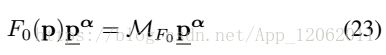相机姿态估计（五）--DLS

论文：A Direct Least-Squares (DLS) Method for PnP

求解过程看着挺吃力的，看懂的还请多多指正。

本文针对PnP问题，采用非线性最小二乘直接计算，主要贡献如下：

1.提出通用的n点（n≥3）姿态（all pose）计算方法，设计了独特的非线性最小二乘代价函数。

2.无初始化要求，性能接近极大似然（MLE）方法的结果

3.非线性最小二乘代价函数不依赖点数变化。

具体过程如下：

1.问题建模

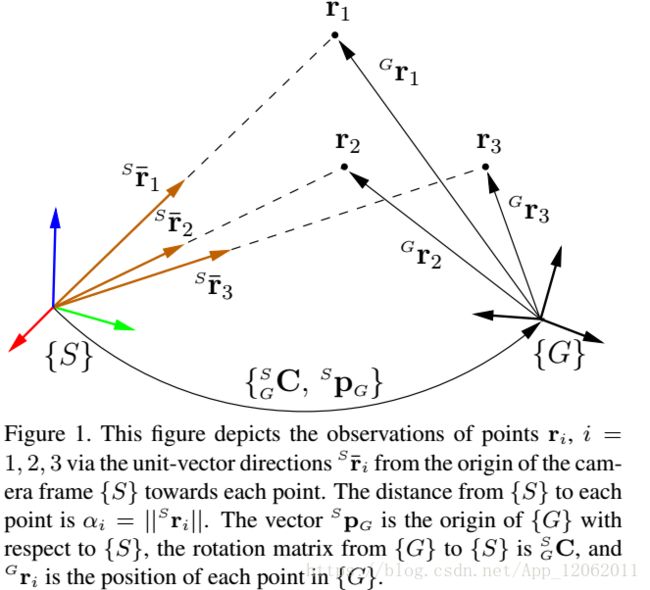
这里的定义，跟其他如AP3P是一样的，就是换了个字符，S是sensor的意思，就是相机坐标系，G还是参考坐标系。z是像素坐标系中测量点的方向向量，后面是噪声。C还是旋转矩阵，P是平移向量，下图是PnP问题最轻量化的描述。

整体的PnP非线性最小二乘求解建模如下：

其中代价函数J是均方误差和：

难点在于如何求解J的最小值，通常有给定一个参数的初始猜测值，然后不断迭代如（如GN算法），但这不能保证一定会获得精确值，还有利用KKT条件（SVM中的支持向量的求解算法中有用到）来求非线性系统，但是，这里难点在于位置参数过多（6+n）,而本文提出的方法如下：

1.修改LS模型：

先考虑无噪声情况：

其中未知参数有α，C,P，我们重写成矩阵运算形式：

根据上面，计算P和α：

 注意，P和α，都是旋转矩阵C的线性函数：

因此，我们重写式子4：

 这样，我们将未知参数，从6+n减少到了3。

接着，我们采用CGR 参数化旋转矩阵C，使得3个CGR变量成为无约束优化变量。同时满足：

CGR参数化C（s=[s1,s2,s3]^T）：

 因此，9式可以表示 为：

由于C（s）导致线性化，因此，继续简化：

式13就是最终化简后的约束条件。

2.修改代价函数

利用13式，我们重新定义代价函数J，来计算CGR的旋转参数s,先增加噪声：

 基于15式，PnP问题，重构为下面无约束的LSM问题：

其中，新的定义为： 

 注意，这里是一个4阶多项式，包含如1，s1,s2,s3,...s1^4,s2^4,s3^4等项。

下面介绍作者直接计算多项式最小值的过程：

考虑到目标函数3个位置参数的4阶多项式，因此，优化方程定义为：

为了构造Maculy矩阵，作者对目标函数增加了i=0项，F0= u0 + u1s1 + u2s2+ u3s3,这里u是随机生成的，这样，原始目标函数被扩展为7个单项式组成：

然后 ，作者将参数S集合，划分为4个集合，其中，S3集合包含所有可以被 s3^3整除的项，S2集合包含所有可以被s2^3整除但不能是s3^3，以此类推，S0集合包含所有未划分的剩余项。

之后，扩展多项式Fi为Gi:

假定原始系统的解为p，则所有扩展自F的多项式G，都为0，即F(p) = 0.但是，F0不会是0:

矩阵分解式21:

最终：

 其中：

从式23可以看出，F0（p）是Mf0的一个特征值，对应的特征向量p^α。我们可以直接获得式18的27个解。

因为S0是1，因此将特征向量以第一个项归一化，以此求解出S1,S2,S3。

实际上，这27组解，只有4个是真实局部最优，大多数情况下，n≥6时，我们只能获取一个真实解。之后，根据该解计算代价，如此实现直接计算最优化。

另外，DLS-LM是在上面求解时，采用LM迭代算法，其他与DLS类似。

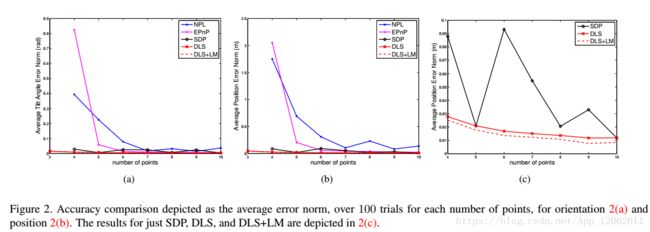
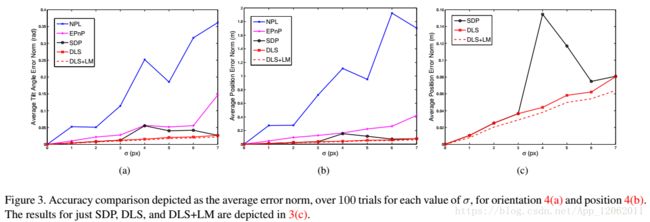
作者对比了NPL,SDP,EPnP,DLS,DLS-LM等算法，点的分布视角45°*45°，并模拟了高斯噪声。效果如下：

从这里可以看出，NPL,SDP基本不用考虑了。当点数超过6时，DLS与EPnP的差距也不明显了，剩下的可以对比下时间。