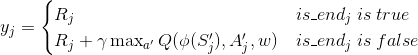系统学习深度学习(三十)--Deep Q-Learning
转自:https://www.cnblogs.com/pinard/p/9714655.html
1. 为何需要价值函数的近似表示
在之前讲到了强化学习求解方法,无论是动态规划DP,蒙特卡罗方法MC,还是时序差分TD,使用的状态都是离散的有限个状态集合S。此时问题的规模比较小,比较容易求解。但是假如我们遇到复杂的状态集合呢?甚至很多时候,状态是连续的,那么就算离散化后,集合也很大,此时我们的传统方法,比如Q-Learning,根本无法在内存中维护这么大的一张Q表。
比如经典的冰球世界(PuckWorld) 强化学习问题,具体的动态demo见这里。环境由一个正方形区域构成代表着冰球场地,场地内大的圆代表着运动员个体,小圆代表着目标冰球。在这个正方形环境中,小圆会每隔一定的时间随机改变在场地的位置,而代表个体的大圆的任务就是尽可能快的接近冰球目标。大圆可以操作的行为是在水平和竖直共四个方向上施加一个时间步时长的一个大小固定的力,借此来改变大圆的速度。环境会在每一个时间步内告诉个体当前的水平与垂直坐标、当前的速度在水平和垂直方向上的分量以及目标的水平和垂直坐标共6项数据,奖励值为个体与目标两者中心距离的负数,也就是距离越大奖励值越低且最高奖励值为0。
在这个问题中,状态是一个6维的向量,并且是连续值。没法直接用之前离散集合的方法来描述状态。当然,你可以说,我们可以把连续特征离散化。比如把这个冰球场100x100的框按1x1的格子划分成10000个格子,那么对于运动员的坐标和冰球的坐标就有25∗25=21025∗25=210次种,如果再加上个体速度的分量就更是天文数字了,此时之前讲过的强化学习方法都会因为问题的规模太大而无法使用。怎么办呢?必须要对问题的建模做修改了,而价值函数的近似表示就是一个可行的方法。
2. 价值函数的近似表示方法
由于问题的状态集合规模大,一个可行的建模方法是价值函数的近似表示。方法是我们引入一个状态价值函数v̂ , 这个函数由参数w描述,并接受状态s作为输入,计算后得到状态s的价值,即我们期望:
v̂ (s,w)≈vπ(s)
类似的,引入一个动作价值函数q̂ ,这个函数由参数w描述,并接受状态s与动作a作为输入,计算后得到动作价值,即我们期望:
q̂ (s,a,w)≈qπ(s,a)
价值函数近似的方法很多,比如最简单的线性表示法,用ϕ(s)表示状态s的特征向量,则此时我们的状态价值函数可以近似表示为:
v̂ (s,w)=ϕ(s)Tw
当然,除了线性表示法,我们还可以用决策树,最近邻,傅里叶变换,神经网络来表达我们的状态价值函数。而最常见,应用最广泛的表示方法是神经网络。因此后面我们的近似表达方法如果没有特别提到,都是指的神经网络的近似表示。
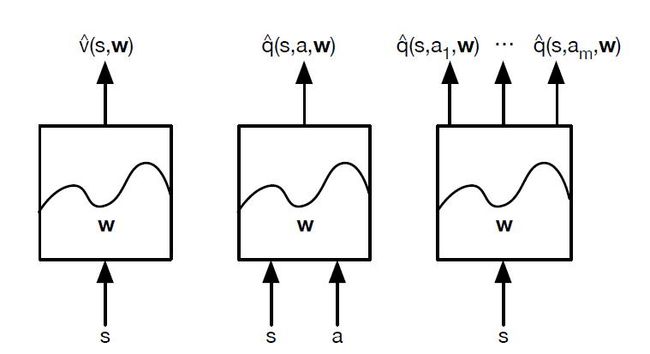
对于神经网络,可以使用DNN,CNN或者RNN。没有特别的限制。如果把我们计算价值函数的神经网络看做一个黑盒子,那么整个近似过程可以看做下面这三种情况:
对于状态价值函数,神经网络的输入是状态s的特征向量,输出是状态价值v̂ (s,w)。对于动作价值函数,有两种方法,一种是输入状态s的特征向量和动作a,输出对应的动作价值q̂ (s,a,w),另一种是只输入状态s的特征向量,动作集合有多少个动作就有多少个输出q̂ (s,ai,w)。这里隐含了我们的动作是有限个的离散动作。
对于我们前一篇系统学习机器学习之增强学习(六)--马尔可夫决策过程策略TD求解(Q-learning)讲到的Q-Learning算法,我们现在就价值函数的近似表示来将其改造,采用上面右边的第三幅图的动作价值函数建模思路来做,现在我们叫它Deep Q-Learning。
3. Deep Q-Learning算法思路
Deep Q-Learning算法的基本思路来源于Q-Learning。但是和Q-Learning不同的地方在于,它的Q值的计算不是直接通过状态值s和动作来计算,而是通过上面讲到的Q网络来计算的。这个Q网络是一个神经网络,我们一般简称Deep Q-Learning为DQN。
DQN的输入是我们的状态s对应的状态向量ϕ(s), 输出是所有动作在该状态下的动作价值函数Q。Q网络可以是DNN,CNN或者RNN,没有具体的网络结构要求。
DQN主要使用的技巧是经验回放(experience replay),即将每次和环境交互得到的奖励与状态更新情况都保存起来,用于后面目标Q值的更新。为什么需要经验回放呢?我们回忆一下Q-Learning,它是有一张Q表来保存所有的Q值的当前结果的,但是DQN是没有的,那么在做动作价值函数更新的时候,就需要其他的方法,这个方法就是经验回放。
通过经验回放得到的目标Q值和通过Q网络计算的Q值肯定是有误差的,那么我们可以通过梯度的反向传播来更新神经网络的参数w,当w收敛后,我们的就得到的近似的Q值计算方法,进而贪婪策略也就求出来了。
下面我们总结下DQN的算法流程,基于NIPS 2013 DQN。
算法输入:迭代轮数T,状态特征维度n, 动作集A, 步长α,衰减因子γ, 探索率ϵ, Q网络结构, 批量梯度下降的样本数m。
输出:Q网络参数
1. 随机初始化Q网络的所有参数w,基于w初始化所有的状态和动作对应的价值Q。清空经验回放的集合D。
2. for i from 1 to T,进行迭代。
a) 初始化S为当前状态序列的第一个状态, 拿到其特征向量ϕ(S)
b) 在Q网络中使用ϕ(S)作为输入,得到Q网络的所有动作对应的Q值输出。用ϵ−贪婪法在当前Q值输出中选择对应的动作A
c) 在状态S执行当前动作A,得到新状态S′对应的特征向量ϕ(S′)和奖励R$,是否终止状态is_end
d) 将{ϕ(S),A,R,ϕ(S′),is_end}这个五元组存入经验回放集合D
e) S=S′
f) 从经验回放集合D中采样m个样本{ϕ(Sj),Aj,Rj,ϕ(S′j),is_endj},j=1,2.,,,m,计算当前目标Q值yj:
g) 使用均方差损失函数 ,通过神经网络的梯度反向传播来更新Q网络的所有参数w
,通过神经网络的梯度反向传播来更新Q网络的所有参数w
h) 如果S′是终止状态,当前轮迭代完毕,否则转到步骤b)
注意,上述第二步的f步和g步的Q值计算也都需要通过Q网络计算得到。另外,实际应用中,为了算法较好的收敛,探索率ϵ需要随着迭代的进行而变小。
4. Deep Q-Learning实例
下面我们用一个具体的例子来演示DQN的应用。这里使用了OpenAI Gym中的CartPole-v0游戏来作为我们算法应用。CartPole-v0游戏的介绍参见这里。它比较简单,基本要求就是控制下面的cart移动使连接在上面的pole保持垂直不倒。这个任务只有两个离散动作,要么向左用力,要么向右用力。而state状态就是这个cart的位置和速度, pole的角度和角速度,4维的特征。坚持到200分的奖励则为过关。
完整的代码参见我的github: https://github.com/ljpzzz/machinelearning/blob/master/reinforcement-learning/dqn.py
代码参考了知乎上的一个DQN实例,修改了代码中的一些错误,并用最新的Python3.6+Tensorflow1.8.0运行。要跑代码需要安装OpenAI的Gym库,使用"pip install gym"即可。
代码使用了一个三层的神经网络,输入层,一个隐藏层和一个输出层。下面我们看看关键部分的代码。
算法第2步的步骤b通过ϵ−贪婪法选择动作的代码如下,注意每次我们ϵ−贪婪法后都会减小ϵ值。
![]()
def egreedy_action(self,state):
Q_value = self.Q_value.eval(feed_dict = {
self.state_input:[state]
})[0]
if random.random() <= self.epsilon:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return random.randint(0,self.action_dim - 1)
else:
self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
return np.argmax(Q_value)
算法第2步的步骤c在状态S执行当前动作A的代码如下,这个交互是由Gym完成的。
next_state,reward,done,_ = env.step(action)
# Define reward for agent
reward = -1 if done else 0.1算法第2步的步骤d保存经验回放数据的代码如下:
def perceive(self,state,action,reward,next_state,done):
one_hot_action = np.zeros(self.action_dim)
one_hot_action[action] = 1
self.replay_buffer.append((state,one_hot_action,reward,next_state,done))
if len(self.replay_buffer) > REPLAY_SIZE:
self.replay_buffer.popleft()
if len(self.replay_buffer) > BATCH_SIZE:
self.train_Q_network()
算法第2步的步骤f,g计算目标Q值,并更新Q网络的代码如下:
def train_Q_network(self):
self.time_step += 1
# Step 1: obtain random minibatch from replay memory
minibatch = random.sample(self.replay_buffer,BATCH_SIZE)
state_batch = [data[0] for data in minibatch]
action_batch = [data[1] for data in minibatch]
reward_batch = [data[2] for data in minibatch]
next_state_batch = [data[3] for data in minibatch]
# Step 2: calculate y
y_batch = []
Q_value_batch = self.Q_value.eval(feed_dict={self.state_input:next_state_batch})
for i in range(0,BATCH_SIZE):
done = minibatch[i][4]
if done:
y_batch.append(reward_batch[i])
else :
y_batch.append(reward_batch[i] + GAMMA * np.max(Q_value_batch[i]))
self.optimizer.run(feed_dict={
self.y_input:y_batch,
self.action_input:action_batch,
self.state_input:state_batch
})
我们在每100轮迭代完后会去玩10次交互测试,计算10次的平均奖励。运行了代码后,我的3000轮迭代的输出如下:
episode: 0 Evaluation Average Reward: 12.2
episode: 100 Evaluation Average Reward: 9.4
episode: 200 Evaluation Average Reward: 10.4
episode: 300 Evaluation Average Reward: 10.5
episode: 400 Evaluation Average Reward: 11.6
episode: 500 Evaluation Average Reward: 12.4
episode: 600 Evaluation Average Reward: 29.6
episode: 700 Evaluation Average Reward: 48.1
episode: 800 Evaluation Average Reward: 85.0
episode: 900 Evaluation Average Reward: 169.4
episode: 1000 Evaluation Average Reward: 200.0
episode: 1100 Evaluation Average Reward: 200.0
episode: 1200 Evaluation Average Reward: 200.0
episode: 1300 Evaluation Average Reward: 200.0
episode: 1400 Evaluation Average Reward: 200.0
episode: 1500 Evaluation Average Reward: 200.0
episode: 1600 Evaluation Average Reward: 200.0
episode: 1700 Evaluation Average Reward: 200.0
episode: 1800 Evaluation Average Reward: 200.0
episode: 1900 Evaluation Average Reward: 200.0
episode: 2000 Evaluation Average Reward: 200.0
episode: 2100 Evaluation Average Reward: 200.0
episode: 2200 Evaluation Average Reward: 200.0
episode: 2300 Evaluation Average Reward: 200.0
episode: 2400 Evaluation Average Reward: 200.0
episode: 2500 Evaluation Average Reward: 200.0
episode: 2600 Evaluation Average Reward: 200.0
episode: 2700 Evaluation Average Reward: 200.0
episode: 2800 Evaluation Average Reward: 200.0
episode: 2900 Evaluation Average Reward: 200.0
大概到第1000次迭代后,算法已经收敛,达到最高的200分。当然由于是ϵ−探索,每次前面的输出可能不同,但最后应该都可以收敛到200的分数。当然由于DQN不保证绝对的收敛,所以可能到了200分后还会有抖动。
5. Deep Q-Learning小结
DQN由于对价值函数做了近似表示,因此有了解决大规模强化学习问题的能力。但是DQN有个问题,就是它并不一定能保证Q网络的收敛,也就是说,我们不一定可以得到收敛后的Q网络参数。这会导致我们训练出的模型效果很差。
针对这个问题,衍生出了DQN的很多变种,比如Nature DQN(NIPS 2015), Double DQN,Dueling DQN等。