Python信号分析 | 连续信号的傅立叶变换
1、连续周期信号的傅立叶级数
由傅立叶级数的形式可以看出,其都属于积分形式,故在MATLAB中和Python中均可以用积分函数来实现求解。
例:Python中代码如下:
"""
连续周期信号的傅立叶级数
"""
from sympy import cos,sin
from sympy.abc import t,n,y
from scipy import integrate
import numpy as np
import matplotlib.pyplot as plt
nf=30
T=10
tao=1.0
an=np.zeros(nf)
bn=np.zeros(nf)
cn=np.zeros(nf)
phase=np.zeros(nf)
y=1
half0,err0=integrate.quad(lambda t:y,-tao/2,tao/2)
an[0]=2*half0/T
for n in range(1,nf):
half,err=integrate.quad(lambda t:2*y*cos(2.0/T*np.pi*n*t),-tao/2,tao/2)
an[n]=half/10
half1,err1=integrate.quad(lambda t:2*y*sin(2.0/T*np.pi*n*t),-tao/2,tao/2)
bn[n]=half1/10
cn[n]=np.sqrt(an[n]**2+bn[n]**2)
for i in range(0,nf):
if an[i]>=0:
phase[i]=0
else:
phase[i]=np.pi
k=np.arange(0,nf)
plt.subplot(211)
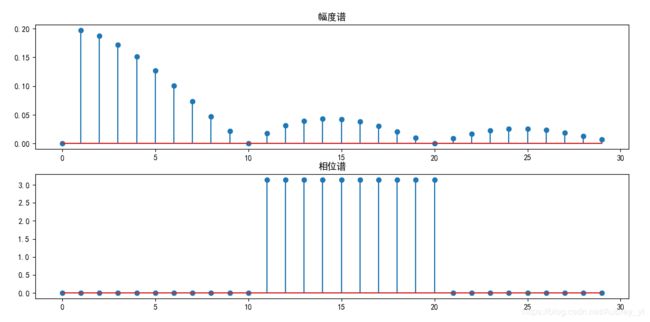
plt.title(u'幅度谱')
plt.stem(k,cn)
plt.subplot(212)
plt.title(u'相位谱')
plt.stem(k,phase)
plt.show()
运行结果:
2、连续非周期信号的傅立叶变换
在MATLAB中实现傅立叶变换的调用格式为:
F=fourier(f)
F是符号函数f的傅立叶变换,默认返回是关于w的函数;
F=fourier(f,v)
F是关于符号对象v的函数,而不是w;
F=fourier(f,u,v)
函数f是关于符号对象u的函数,F是关于符号对象v的函数。
Python中,用fourier_transform函数来实现傅立叶变换,须注意的是,Python运行结果的自变量不是角频率w而是频率f。
例:Python代码如下:
"""
连续非周期信号的傅立叶变换
"""
from sympy import fourier_transform,exp,plot,Heaviside,atan,im,re,pi
from sympy.abc import t,f
ft=exp(-2*t)*Heaviside(t)
F=fourier_transform(ft,t,f)
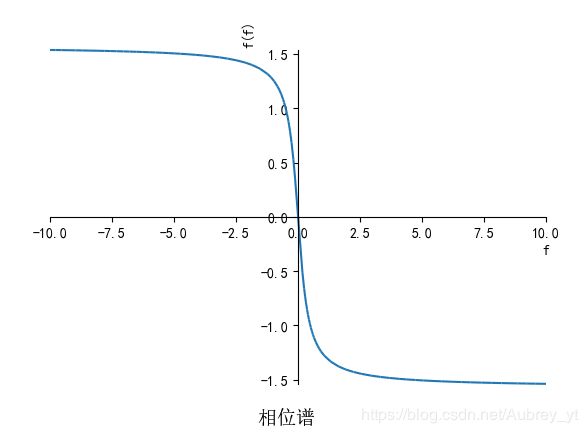
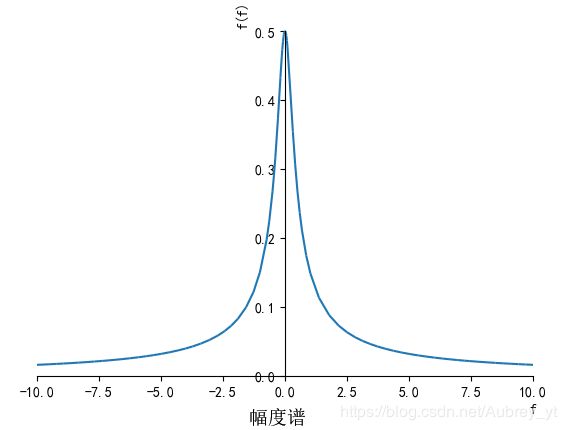
plot(abs(F))
plot(atan(im(F)/re(F)))
运行结果:
3、连续非周期信号的傅立叶逆变换
在MATLAB中,傅立叶逆变换的调用格式为:
f=ifourier(F)
f=ifourier(F,u)
f=ifourier(F,v,u)
在Python中,用inverse_fourier_transform函数来实现傅立叶逆变换。
例:Python中代码如下:
"""
傅立叶逆变换
"""
from sympy import inverse_fourier_transform,exp,sqrt,pi,plot
from sympy.abc import t,f
F=1/(1+(2*pi*f)**2)
ft=inverse_fourier_transform(F,f,t)
plot(abs(F))
plot(ft)