有趣的数组
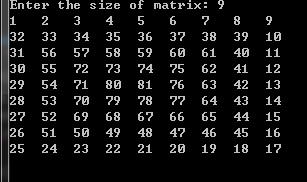
螺旋矩阵
很多面试题都喜欢问这样的问题,解决的方法很简单,把复杂的问题分解成简单的问题。
①把一个矩阵分层,一层一层的解决;
②再分层的基础上,再将一层分成上下左右四个部分单独解决;
只要注意一下数组的边界即可循环完成,有一点需要注意当数组的大小为奇数或是偶数时是有稍许不同的需要注意一下。
#include 1; j++) //处理右面
{
arr[j][n - i - 1] = m++;
}
for (int j = n-i-1; j > i; j--) //处理下面
{
arr[n - i - 1][j] = m++;
}
for (int j = n-i-1; j>i; j--) //处理左面
{
arr[j][i] = m++;
}
}
if (n%2!=0) //若是奇数,补出中心点
{
arr[n / 2][n / 2] = m;
}
for (int i = 0; i < n; i++) //循环打印
{
for (int j = 0; j cout <4)<< arr[i][j];
}
cout << endl;
}
for (int i = 0; i < n; i++) //释放二维数组
{
delete[] arr[i];
}
delete[] arr;
cin.get();
cin.get();
return 0;
} 输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 则依次打印出数字1,2,3,4,8,12,11,10,9,5,6,7
若果要处理的不是一个一直正方形的而是一个长方形的话上面的方法就比较难处理了,因此只需要稍作修改即可
vector<int> printMatrix(vector<vector<int> > matrix)
{
int row = matrix.size();
int col = matrix[0].size();
vector<int> res;
// 输入的二维数组非法,返回空的数组
if (row == 0 || col == 0) return res;
// 定义四个关键变量,表示左上和右下的打印范围
int left = 0, top = 0, right = col - 1, bottom = row - 1;
while (left <= right && top <= bottom)
{
// left to right
for (int i = left; i <= right; ++i) res.push_back(matrix[top][i]);
// top to bottom
for (int i = top + 1; i <= bottom; ++i) res.push_back(matrix[i][right]);
// right to left
if (top != bottom)
for (int i = right - 1; i >= left; --i) res.push_back(matrix[bottom][i]);
// bottom to top
if (left != right)
for (int i = bottom - 1; i > top; --i) res.push_back(matrix[i][left]);
left++,top++,right--,bottom--;
}
return res;
}再来看一个神奇的数组zigzag
在JPEG图像处理算法中首先对图像进行分块,会使用到这个“之”字矩阵,它长成下面这个样子
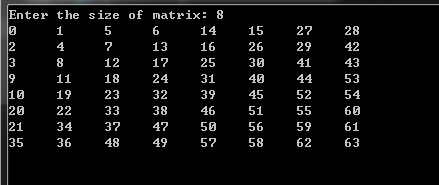
它就像一个蛇一样,一直在沿着对角线绕,一下增加,一下减小很难实现啊,还是一部分一部分来分析。
我们先单独来看看左上部分

这里我们要注意到一件事情,zigzag数组的基本变换单位和普通矩阵不一样,不在是按行或是列变化了,也就是说行数和列数都是变换的,但是在一条斜线上有个关键的性质,横纵坐标之和是相等的,这将成为搞定这个zigzag的突破点。
将每斜开始增长的第一个点叫做跳变点(可能在第一行也可能在第一列,例如1、3、6),那么就会发现跳变点的值等于,在该点之前的元素的个数,比如上图中6这个跳变点,它就等于在它之前的元素的个数6,而6对应的坐标为(0,3)对于坐标和S=i+j=3,而它之前的元素
sum=1+2+3=S∗(S+1)/2
我们解决了一个斜行的初始值的问题,接下来就是要确定一个斜行内的元素是从左下到右上的还是从右上到左下的,其实很好分别,因为是交替出现,利用S的奇偶性即可判断:
①若S为奇数,则是从右上至左下的;
②若S为偶数,则是从左下至右上的;
最后确定准确的数值
我们以(1,2)点为例,我们已经知道它所在斜的初始值为6,并是按照从右上到左下递增的,那么我们只需要知道它的纵坐标是几就是增加了几,因此在左上部分值与坐标的对应关系可以写作
arr[i][j] = s*(s + 1) / 2 + (((i + j) % 2 == 0) ? j: i);因为结构变了 跳转点(13)就无法通过
sum=1+2+3=S∗(S+1)/2
计算了,因此我们不找跳转点了反过来找结束点(12,14)利用这个点反过来算各点的值。
这里可以将最后一个点当成(0,0)点,会比较好理解
s = (n - 1 - i) + (n - 1 - j);
arr[i][j] = squa - s*(s + 1) / 2 - (n - (((i + j) % 2 == 0) ? j : i));这样就完成了
#include //左上部分
{
arr[i][j] = s*(s + 1) / 2 + (((i + j) % 2 == 0) ? j: i);
}
else //右下部分
{
s = (n - 1 - i) + (n - 1 - j);
arr[i][j] = squa - s*(s + 1) / 2 - (n - (((i + j) % 2 == 0) ? j : i));
}
}
}
//
for (int i = 0; i < n; i++) //循环打印
{
for (int j = 0; j < n; j++)
{
cout << left << setw(6) << arr[i][j];
}
cout << endl;
}
for (int i = 0; i < n; i++) //释放二维数组
{
delete[] arr[i];
}
delete[] arr;
cin.sync();
cin.get();
return 0;
}