数据结构与算法之美---CH09---队列

0. 开篇问题

  CPU 资源是有限的，任务的处理速度与线程个数并不是线性正相关。相反，过多的线程反而会导致 CPU 频繁切换，处理性能下降。所以，线程池的大小一般都是综合考虑要处理任务的特点和硬件环境，来事先设置的。
  当我们向固定大小的线程池中请求一个线程时，如果线程池中没有空闲资源了，这个时候线程池如何处理这个请求？是拒绝请求还是排队请求？各种处理策略又是怎么实现的呢？

1. 什么是队列？

1. 队列和栈一样，也是一种操作受限的线性表。
2. 先进者先出，这就是典型的“队列”结构。
3. 支持两个基本操作：入队enqueue()；出队dequeue()。

2. 为什么需要队列？

  相比数组和链表，队列带来的只有限制，并没有任何优势。那直接使用数组或者链表不就好了吗？为什么还要用这个“操作受限”的“队列”呢？
  这里的解释和为什么需要栈类似。

1. 数组和链表确实能够替代队列
2. 特定的数据结构是对特定场景的抽象
3. 软件开发中，不是暴露越多接口越好，操作灵活会带来不可控。一句话“有限制，才自由”，这是软件开发的特点。

  因此，当某个数据集合只涉及一端插入数据，另一端删除数据，并且满足先进先出的特性，应该首选“队列”这种数据结构。

3. 如何实现一个队列？

实现一个队列，必须要实现队列的接口。

public interface QueueInterface {
    boolean enqueue(T item);
    T dequeue();
}

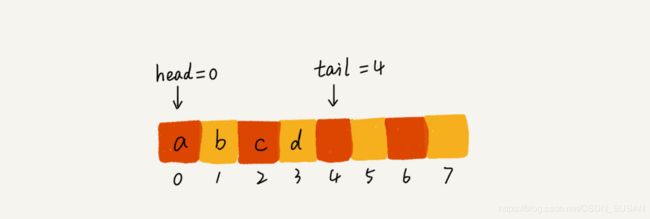
3.1 顺序队列

顺序队列操作表示如下图：

1. 当连续入队4个元素时候。
   2. 当出队两个元素
   

实现代码如下：

public class ArrayQueue implements QueueInterface {
    int LEN = 3;
    T[] items = (T[]) new Object[LEN];
    int head;
    int tail;
    @Override
    public boolean enqueue(T item) {
        if (tail >= LEN) {
            return false;
        }
        items[tail++] = item;
        return true;
    }

    @Override
    public T dequeue() {
        if (head == tail) {
            return null;
        }
        return items[head++];
    }
}

出队入队时间复杂度：O(1)
出队入队空间复杂度：O(1)
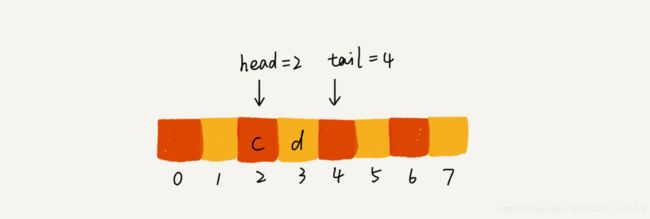
  随着不停地入队、出队操作，head 和 tail 都会持续往后移动。当 tail 移动到最右边，即使数组中还有空闲空间，也无法继续往队列中添加数据了。这个问题该如何解决呢？
  在数组一节，也遇到过类似问题，就是数组的删除操作会导致数组中的数据不连续。还记当时是怎么解决的吗？对，用数据搬移！但是每次进行出队操作相当于删除数组下标为 0 的数据，然后要搬移数据，这样出队时间复杂度就会从原来的 O(1) 变为 O(n)。能不能优化一下呢？
  实际上，在出队时可以不用搬移数据。如果没有空闲空间了，我们只需要在入队时，再集中触发一次数据的搬移操作。借助这个思想，出队函数 dequeue() 保持不变，我们稍加改造一下入队函数 enqueue() 的实现，就可以轻松解决刚才的问题了。下面是具体的代码：

public boolean enqueue(T item) {
        if (tail >= LEN) {
            if (head == 0) {
                Utils.println("really no space");
                return false;
            }
            for (int i = head; i < tail; i++) {
                items[i-head] = items[i];
            }
            tail = tail - head;
            head = 0;
        }
        items[tail++] = item;
        return true;
    }

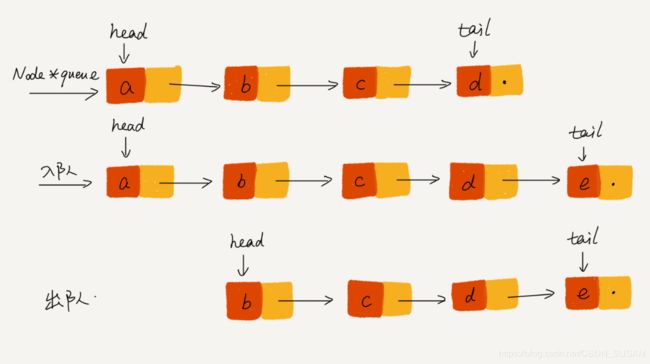
3.2 链式队列

基于链表的实现方式如图：

实现代码如下：

public class LinkQueue implements QueueInterface {
    private class Node {
        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }

        T item;
        Node next;
    }
    Node tail = null;
    Node head = null;
    @Override
    public boolean enqueue(T item) {
        Node newNode = new Node(item, null);

        if (tail == null) {
            tail = newNode;
        } else {
            tail.next = newNode;
            tail = newNode;
        }
        if (head == null) {
            head = newNode;
        }
        return true;
    }

    @Override
    public T dequeue() {
        if (head == null) {
            return null;
        }
        T tmp = head.item;
        head = head.next;
        return tmp;
    }
}

出队入队时间复杂度：O(1)
出队入队空间复杂度：O(1)

4. 几种特殊的队列

4.1 循环队列

  刚才用数组来实现队列的时候，在 tail==n 时，会有数据搬移操作，这样入队操作性能就会受到影响。那有没有办法能够避免数据搬移呢？来看看循环队列的解决思路。
如下图：

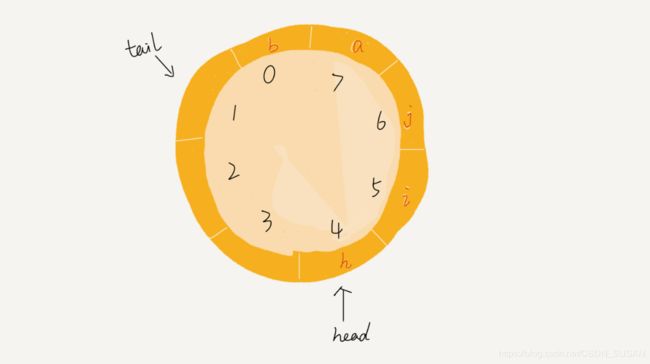
  可以看到，图中这个队列的大小为 8，当前 head=4，tail=7。当有一个新的元素 a 入队时，我们放入下标为 7 的位置。但这个时候，我们并不把 tail 更新为 8，而是将其在环中后移一位，到下标为 0 的位置。当再有一个元素 b 入队时，我们将 b 放入下标为 0 的位置，然后 tail 加 1 更新为 1。
  通过该方法，成功避免了数据搬移操作。看起来不难理解，但是循环队列的代码实现难度要难多了。要想写出 bug free 的循环队列最关键的是确定好队空和队满的判定条件。

1. 队空的条件依然是head == tail。
2. 队满的条件(tail+1)%n=head。

代码实现如下：

public class CricleQueue implements QueueInterface {
    int LEN = 10;
    T[] items = (T[]) new Object[LEN];
    int head;
    int tail;

    @Override
    public boolean enqueue(T item) {
        if ((tail + 1) % LEN == head) {
            Utils.print("no space");
            return false;
        }
        items[tail] = item;
        tail = (tail + 1) % LEN;
        return false;
    }

    @Override
    public T dequeue() {
        if (head == tail) {
            return null;
        }
        T tmp = items[head];
        head = (head + 1) % LEN;
        return tmp;
    }
}

4.2 阻塞队列

阻塞队列其实就是在队列基础上增加了阻塞操作。

1. 在队列为空的时，从队头取数据会被阻塞。因为此时还没有数据可取，直到队列中有了数据才能返回；
2. 队列已经满了，插入数据就会被阻塞，直到队列中有空闲位置后再插入数据，然后再返回。

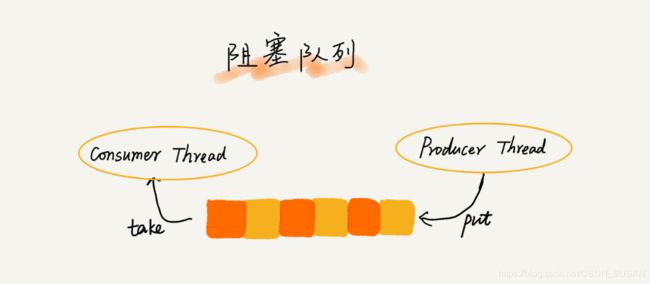
  上述的定义就是一个“生产者 - 消费者模型”！是的，我们可以使用阻塞队列，轻松实现一个“生产者 - 消费者模型”！
  我们还可以通过协调“生产者”和“消费者”的个数，来提高数据的处理效率。比如前面的例子，我们可以多配置几个“消费者”，来应对一个“生产者”。

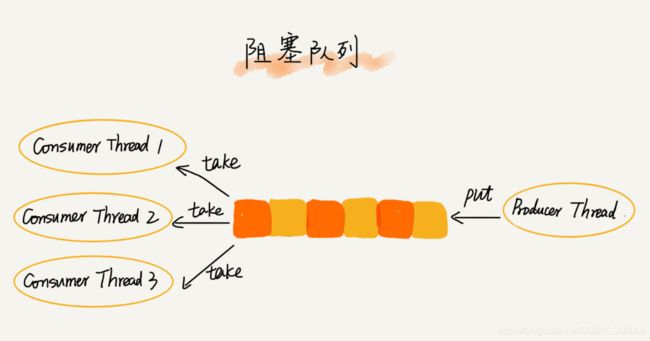
4.3 并发队列

  线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁，但是锁粒度大并发度会比较低，同一时刻仅允许一个存或者取操作。
  实际上，基于数组的循环队列，利用 CAS 原子操作，可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。

5. 解开篇答

  线程池没有空闲线程时，新的任务请求线程资源时，线程池该如何处理？各种处理策略又是如何实现的呢？
一般有两种处理策略。

1. 第一种是非阻塞的处理方式，直接拒绝任务请求；
2. 另一种是阻塞的处理方式，将请求排队，等到有空闲线程时，取出排队的请求继续处理。

如何存储排队的请求呢？

1. 基于链表实现，支持无限排队的无界队列（unbounded queue），但会导致过多的请求排队，请求处理的响应时间过长。所以响应时间比较敏感的系统，基于链表实现的线程池是不合适的。
2. 基于数组实现有界队列（bounded queue），线程池中排队的请求超过队列大小时，后续请求会被拒绝，对响应时间敏感的系统来说，相对更合理。
   不过设置合理的队列大小，非常有讲究。队列太大导致等待的请求太多，队列太小会导致无法充分利用系统资源、发挥最大性能。

  队列除了应用在线程池请求排队的场景之外，队列可以应用在任何有限资源池中，用于排队请求，比如数据库连接池等。实际上，对于大部分资源有限的场景，当没有空闲资源时，基本上都可以通过“队列”这种数据结构来实现请求排队。

6. 课后思考

除了线程池这种池结构会用到队列排队请求，还有哪些类似线程池结构或者场景中会用到队列的排队请求呢？

1. 像windows操作系统的消息队列，略高级一些带有优先级。还有qt中的信号与槽函数机制，使用connect链接，其中的参数就是设置为把窗口界面消息放到消息队列，然后一次取出。比如优先级消息，窗口系统关闭，优先级高，则就直接执行关闭操作。
2. sockets网络连接队列。
3. 数据库连接队列。
4. 一种集群操作，很多客户端像服务端请求资源，处理高并发大量请求。把这些请求放到队列中。
5. 分布式应用中的消息队列，也是一种队列结构。

今天讲到并发队列，关于如何实现无锁的并发队列，网上有很多讨论。对这个问题，你怎么看？
  考虑使用CAS实现无锁队列，则在入队前，获取tail位置，入队时比较tail是否发生变化，如果否，则允许入队，反之，本次入队失败。出队则是获取head位置，进行cas。