语义分割常用loss介绍及pytorch实现

这里介绍语义分割常用的loss函数，附上pytorch实现代码。

Log loss

交叉熵，二分类交叉熵的公式如下：

pytorch代码实现：

#二值交叉熵，这里输入要经过sigmoid处理
import torch
import torch.nn as nn
import torch.nn.functional as F
nn.BCELoss(F.sigmoid(input), target)
#多分类交叉熵, 用这个 loss 前面不需要加 Softmax 层
nn.CrossEntropyLoss(input, target)

Dice loss

Dice loss是针对前景比例太小的问题提出的，dice系数源于二分类，本质上是衡量两个样本的重叠部分。公式如下：

Dice Loss = 1 - DSC，pytorch代码实现：

import torch
import torch.nn as nn
 
class DiceLoss(nn.Module):
	def __init__(self):
		super(DiceLoss, self).__init__()
 
	def	forward(self, input, target):
		N = target.size(0)
		smooth = 1
 
		input_flat = input.view(N, -1)
		target_flat = target.view(N, -1)
 
		intersection = input_flat * target_flat
 
		loss = 2 * (intersection.sum(1) + smooth) / (input_flat.sum(1) + target_flat.sum(1) + smooth)
		loss = 1 - loss.sum() / N
 
		return loss
 
class MulticlassDiceLoss(nn.Module):
	"""
	requires one hot encoded target. Applies DiceLoss on each class iteratively.
	requires input.shape[0:1] and target.shape[0:1] to be (N, C) where N is
	  batch size and C is number of classes
	"""
	def __init__(self):
		super(MulticlassDiceLoss, self).__init__()
 
	def forward(self, input, target, weights=None):
 
		C = target.shape[1]
 
		# if weights is None:
		# 	weights = torch.ones(C) #uniform weights for all classes
 
		dice = DiceLoss()
		totalLoss = 0
 
		for i in range(C):
			diceLoss = dice(input[:,i], target[:,i])
			if weights is not None:
				diceLoss *= weights[i]
			totalLoss += diceLoss
 
		return totalLoss

IOU loss

IOU loss和Dice loss有点类似，IOU表示如下：

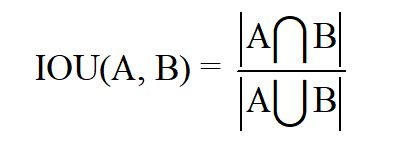
Soft_IOU_loss pytorch代码实现：

#针对多分类问题，二分类问题更简单一点。
import torch
import torch.nn as nn
import torch.nn.functional as F

class SoftIoULoss(nn.Module):
    def __init__(self, n_classes):
        super(SoftIoULoss, self).__init__()
        self.n_classes = n_classes

    @staticmethod
    def to_one_hot(tensor, n_classes):
        n, h, w = tensor.size()
        one_hot = torch.zeros(n, n_classes, h, w).scatter_(1, tensor.view(n, 1, h, w), 1)
        return one_hot

    def forward(self, input, target):
        # logit => N x Classes x H x W
        # target => N x H x W

        N = len(input)

        pred = F.softmax(input, dim=1)
        target_onehot = self.to_one_hot(target, self.n_classes)

        # Numerator Product
        inter = pred * target_onehot
        # Sum over all pixels N x C x H x W => N x C
        inter = inter.view(N, self.n_classes, -1).sum(2)

        # Denominator
        union = pred + target_onehot - (pred * target_onehot)
        # Sum over all pixels N x C x H x W => N x C
        union = union.view(N, self.n_classes, -1).sum(2)

        loss = inter / (union + 1e-16)

        # Return average loss over classes and batch
        return -loss.mean()

IOU loss 和 Dice loss训练过程可能出现不太稳定的情况。

Lovasz-Softmax loss

Lovasz-Softmax loss是在CVPR2018提出的针对IOU优化设计的loss，比赛里用一下有奇效，数学推导已经超出笔者所知范围，有兴趣的可以围观一下论文。虽然理解起来比较难，但是用起来还是比较容易的。总的来说，就是对Jaccard loss 进行 Lovasz扩展，loss表现更好一点。
另外，作者在github答疑时表示由于该Lovasz softmax优化针对的是image-level mIoU，因此较小的batchsize训练对常用的dataset-level mIoU的性能表现会有损害。以及该loss适用于finetuning过程。将其与其它loss加权使用，会有比较好的效果。
代码解读：
作者给出了二分类和多分类的loss计算，个人觉得三步走：

• 计算每个像素errors，二分类里用的hinge算的errors，多分类直接计算预测值和真实值的差；
• 根据errors的排序，对labels排序，进而算Jaccard grad（代码里的lovasz_grad函数）；
• 结合errors和Jaccard grad得到所求loss。

pytorch代码实现(摘自作者GitHub):

import torch
from torch.autograd import Variable
import torch.nn.functional as F
import numpy as np

def lovasz_grad(gt_sorted):
    """
    Computes gradient of the Lovasz extension w.r.t sorted errors
    See Alg. 1 in paper
    """
    p = len(gt_sorted)
    gts = gt_sorted.sum()
    intersection = gts - gt_sorted.float().cumsum(0)
    union = gts + (1 - gt_sorted).float().cumsum(0)
    jaccard = 1. - intersection / union
    if p > 1: # cover 1-pixel case
        jaccard[1:p] = jaccard[1:p] - jaccard[0:-1]
    return jaccard
# --------------------------- BINARY LOSSES ---------------------------
def lovasz_hinge(logits, labels, per_image=True, ignore=None):
    """
    Binary Lovasz hinge loss
      logits: [B, H, W] Variable, logits at each pixel (between -\infty and +\infty)
      labels: [B, H, W] Tensor, binary ground truth masks (0 or 1)
      per_image: compute the loss per image instead of per batch
      ignore: void class id
    """
    if per_image:
        loss = mean(lovasz_hinge_flat(*flatten_binary_scores(log.unsqueeze(0), lab.unsqueeze(0), ignore))
                          for log, lab in zip(logits, labels))
    else:
        loss = lovasz_hinge_flat(*flatten_binary_scores(logits, labels, ignore))
    return loss
    
def lovasz_hinge_flat(logits, labels):
    """
    Binary Lovasz hinge loss
      logits: [P] Variable, logits at each prediction (between -\infty and +\infty)
      labels: [P] Tensor, binary ground truth labels (0 or 1)
      ignore: label to ignore
    """
    if len(labels) == 0:
        # only void pixels, the gradients should be 0
        return logits.sum() * 0.
    signs = 2. * labels.float() - 1.
    errors = (1. - logits * Variable(signs))
    errors_sorted, perm = torch.sort(errors, dim=0, descending=True)
    perm = perm.data
    gt_sorted = labels[perm]
    grad = lovasz_grad(gt_sorted)
    loss = torch.dot(F.relu(errors_sorted), Variable(grad))
    return loss
    
def flatten_binary_scores(scores, labels, ignore=None):
    """
    Flattens predictions in the batch (binary case)
    Remove labels equal to 'ignore'
    """
    scores = scores.view(-1)
    labels = labels.view(-1)
    if ignore is None:
        return scores, labels
    valid = (labels != ignore)
    vscores = scores[valid]
    vlabels = labels[valid]
    return vscores, vlabels

# --------------------------- MULTICLASS LOSSES ---------------------------
def lovasz_softmax(probas, labels, classes='present', per_image=False, ignore=None):
    """
    Multi-class Lovasz-Softmax loss
      probas: [B, C, H, W] Variable, class probabilities at each prediction (between 0 and 1).
              Interpreted as binary (sigmoid) output with outputs of size [B, H, W].
      labels: [B, H, W] Tensor, ground truth labels (between 0 and C - 1)
      classes: 'all' for all, 'present' for classes present in labels, or a list of classes to average.
      per_image: compute the loss per image instead of per batch
      ignore: void class labels
    """
    if per_image:
        loss = mean(lovasz_softmax_flat(*flatten_probas(prob.unsqueeze(0), lab.unsqueeze(0), ignore), classes=classes)
                          for prob, lab in zip(probas, labels))
    else:
        loss = lovasz_softmax_flat(*flatten_probas(probas, labels, ignore), classes=classes)
    return loss


def lovasz_softmax_flat(probas, labels, classes='present'):
    """
    Multi-class Lovasz-Softmax loss
      probas: [P, C] Variable, class probabilities at each prediction (between 0 and 1)
      labels: [P] Tensor, ground truth labels (between 0 and C - 1)
      classes: 'all' for all, 'present' for classes present in labels, or a list of classes to average.
    """
    if probas.numel() == 0:
        # only void pixels, the gradients should be 0
        return probas * 0.
    C = probas.size(1)
    losses = []
    class_to_sum = list(range(C)) if classes in ['all', 'present'] else classes
    for c in class_to_sum:
        fg = (labels == c).float() # foreground for class c
        if (classes is 'present' and fg.sum() == 0):
            continue
        if C == 1:
            if len(classes) > 1:
                raise ValueError('Sigmoid output possible only with 1 class')
            class_pred = probas[:, 0]
        else:
            class_pred = probas[:, c]
        errors = (Variable(fg) - class_pred).abs()
        errors_sorted, perm = torch.sort(errors, 0, descending=True)
        perm = perm.data
        fg_sorted = fg[perm]
        losses.append(torch.dot(errors_sorted, Variable(lovasz_grad(fg_sorted))))
    return mean(losses)

def flatten_probas(probas, labels, ignore=None):
    """
    Flattens predictions in the batch
    """
    if probas.dim() == 3:
        # assumes output of a sigmoid layer
        B, H, W = probas.size()
        probas = probas.view(B, 1, H, W)
    B, C, H, W = probas.size()
    probas = probas.permute(0, 2, 3, 1).contiguous().view(-1, C)  # B * H * W, C = P, C
    labels = labels.view(-1)
    if ignore is None:
        return probas, labels
    valid = (labels != ignore)
    vprobas = probas[valid.nonzero().squeeze()]
    vlabels = labels[valid]
    return vprobas, vlabels

Focal loss

Focal loss是何恺明针对训练样本不平衡提出的loss 函数。公式：

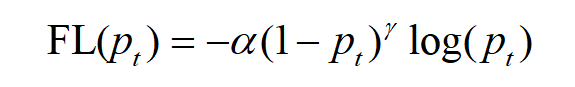
可以认为，focal loss是交叉熵上的变种，针对以下两个问题设计了两个参数$\alpha$、$\beta$：

• 正负样本不平衡，比如负样本太多；
• 存在大量的简单易分类样本。

第一个问题，容易想到可以在loss函数中，给不同类别的样本loss加权重，正样本少，就加大正样本loss的权重，这就是focal loss里面参数 $\alpha$的作用；第二个问题，设计了参数$\beta$，从公式里就可以看到，当样本预测值pt比较大时，也就是易分样本，（1-pt)^beta 会很小，这样易分样本的loss会显著减小，模型就会更关注难分样本loss的优化。
pytorch 代码实现：

import torch
import torch.nn as nn
# --------------------------- BINARY LOSSES ---------------------------
class FocalLoss(nn.Module):
    def __init__(self, alpha=0.25, gamma=2, weight=None, ignore_index=255):
        super(FocalLoss, self).__init__()
        self.alpha = alpha
        self.gamma = gamma
        self.weight = weight
        self.ignore_index = ignore_index
        self.bce_fn = nn.BCEWithLogitsLoss(weight=self.weight)

    def forward(self, preds, labels):
        if self.ignore_index is not None:
            mask = labels != self.ignore
            labels = labels[mask]
            preds = preds[mask]

        logpt = -self.bce_fn(preds, labels)
        pt = torch.exp(logpt)
        loss = -((1 - pt) ** self.gamma) * self.alpha * logpt
        return loss
# --------------------------- MULTICLASS LOSSES ---------------------------
class FocalLoss(nn.Module):
    def __init__(self, alpha=0.5, gamma=2, weight=None, ignore_index=255):
        super().__init__()
        self.alpha = alpha
        self.gamma = gamma
        self.weight = weight
        self.ignore_index = ignore_index
        self.ce_fn = nn.CrossEntropyLoss(weight=self.weight, ignore_index=self.ignore_index)

    def forward(self, preds, labels):
        logpt = -self.ce_fn(preds, labels)
        pt = torch.exp(logpt)
        loss = -((1 - pt) ** self.gamma) * self.alpha * logpt
        return loss

OHEM

OHEM（online hard example mining)，其实应该算是一种思想，在线困难样本挖掘，即根据loss的大小，选择有较大loss的像素反向传播，较小loss的像素梯度为0。这里提供一份基于focal loss的OHEM样例。
pytorch 代码实现：

def focal_loss(self, output, target, alpha, gamma, OHEM_percent):
        output = output.contiguous().view(-1)
        target = target.contiguous().view(-1)
 
        max_val = (-output).clamp(min=0)
        loss = output - output * target + max_val + ((-max_val).exp() + (-output - max_val).exp()).log()
 
        # This formula gives us the log sigmoid of 1-p if y is 0 and of p if y is 1
        invprobs = F.logsigmoid(-output * (target * 2 - 1))
        focal_loss = alpha * (invprobs * gamma).exp() * loss
 
        # Online Hard Example Mining: top x% losses (pixel-wise). Refer to http://www.robots.ox.ac.uk/~tvg/publications/2017/0026.pdf
        OHEM, _ = focal_loss.topk(k=int(OHEM_percent * [*focal_loss.shape][0]))
        return OHEM.mean()

后续看到有意思的loss会继续更新…

参考：

[1]【LOSS】语义分割的各种loss详解与实现
[2] pytorch: DiceLoss MulticlassDiceLoss
[3] 从loss处理图像分割中类别极度不均衡的状况