离散基础 (16). 赌博分析
1. 问题描述
初始给定赌徒 i i i元,每一次赌赢赢1元,其概率为 α \alpha α,每一次赌输输1元,其概率为 β \beta β,其中 β = 1 − α \beta = 1- \alpha β=1−α。根据赌徒的心理——要么赢完 N N N元再走人,不妨用数学符号描述该事件概率为 P i P_i Pi;要么输光手里的 i i i元再走人,相应地,该事件的概率为 1 − P i 1-P_i 1−Pi问:这两种事件的概率分别为多大?
2. 数学分析
首先,直观地我们有,
G a m e b e x t = { G a m e c u r r e n t + 1 , w h e n α G a m e c u r r e n t − 1 , w h e n β Game_{bext}=\left\{\begin{matrix} {Game_{current}}{\rm{ + 1,when}}\alpha\\ {Game_{current}} - 1,when\beta \end{matrix}\right. Gamebext={Gamecurrent+1,whenαGamecurrent−1,whenβ
因为 α + β = 1 \alpha {\rm{ + }}\beta = 1 α+β=1,我们有,
α P i + β P i = α P i + 1 + β P i − 1 \alpha {P_i} + \beta {P_i} = \alpha {P_{i + 1}} + \beta {P_{i - 1}} αPi+βPi=αPi+1+βPi−1
因为 α , β ∉ { 0 , 1 } \alpha ,\beta \notin \left\{ {\left. {0,1} \right\}} \right. α,β∈/{0,1},我们有,
P i + 1 − P i = β α ( P i − P i − 1 ) {P_{i + 1}} - {P_i} = \frac{\beta }{\alpha }({P_i} - {P_{i - 1}}) Pi+1−Pi=αβ(Pi−Pi−1)
因为 P 0 = 0 {P_0} = 0 P0=0,我们有,
P i + 1 − P i = ( β α ) i P 1 {P_{i + 1}} - {P_i} = {\left( {\frac{\beta }{\alpha }} \right)^i}{P_1} Pi+1−Pi=(αβ)iP1
P i + 1 − P 1 = ∑ k = 1 i ( P k + 1 − P k ) {P_{i + 1}} - {P_1} = \sum\limits_{k = 1}^i {({P_{k + 1}} - {P_k})} Pi+1−P1=k=1∑i(Pk+1−Pk)
P i + 1 − P 1 = ∑ k = 1 i ( ( β α ) k P 1 ) {P_{i + 1}} - {P_1} = \sum\limits_{k = 1}^i {\left( {{{\left( {\frac{\beta }{\alpha }} \right)}^k}{P_1}} \right)} Pi+1−P1=k=1∑i((αβ)kP1)
P i + 1 = P 1 ∑ k = 0 i ( β α ) k {P_{i + 1}} = {P_1}\sum\limits_{k = 0}^i {{{\left( {\frac{\beta }{\alpha }} \right)}^k}} Pi+1=P1k=0∑i(αβ)k
化简后,我们有,
P i = { 1 − ( β α ) i 1 − ( β α ) N , α ! = β i N , α = β P_i=\left\{\begin{matrix} \frac{{1 - {{(\frac{\beta }{\alpha })}^i}}}{{1 - {{\left( {\frac{\beta }{\alpha }} \right)}^N}}},\alpha ! = \beta\\ \frac{i}{N},\alpha = \beta \end{matrix}\right. Pi=⎩⎨⎧1−(αβ)N1−(αβ)i,α!=βNi,α=β
以及,
1 − P i = { 1 − 1 − ( β α ) i 1 − ( β α ) N , α ! = β 1 − i N , α = β 1-P_i = \left\{\begin{matrix} 1 - \frac{{1 - {{(\frac{\beta }{\alpha })}^i}}}{{1 - {{\left( {\frac{\beta }{\alpha }} \right)}^N}}},\alpha ! = \beta\\ 1 - \frac{i}{N},\alpha = \beta \end{matrix}\right. 1−Pi=⎩⎨⎧1−1−(αβ)N1−(αβ)i,α!=β1−Ni,α=β
当一直赌博赌下去的时候,即 lim N → ∞ \lim_{N} \to \infty limN→∞时,
lim N → ∞ 1 − P i = { ( β α ) i , w h e r e β α < 1 1 , w h e n β α ≥ 1 \lim_{N \to \infty}{1-P_i} = \left\{\begin{matrix} \left ( \frac{\beta}{\alpha} \right )^{i},where \frac{\beta }{\alpha } < 1\\ 1,when\frac{\beta }{\alpha } \ge 1 \end{matrix}\right. N→∞lim1−Pi={(αβ)i,whereαβ<11,whenαβ≥1
其中, 1 ≤ i ≤ N − 1 1 \le i \le N - 1 1≤i≤N−1.
3. Results
我们可以从2个方面得到基本数学道理如下:
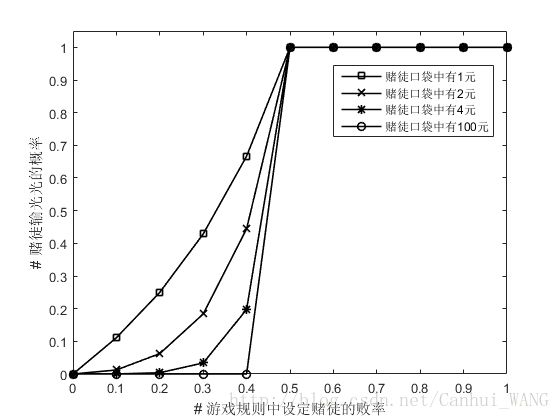
- 不考虑大奖的前提下,如果赔率大于等于50%(日常赌博赔率难道不都是大于50%的么,同意么?),那么,不管你口袋中有多少钱,数学上可以100%保证你最终会输光光。
- 如果一旦大于50%(如果天下有这种好事的话),那么,你口袋中的钱越多,你越有可能成为大满贯,并且可能性是随着你口袋中的钱的数目而指数上升的。
4. 下一步
上面分析的只是赌博的基调(输)。现实生活中,大奖因素会引导赌徒抱有侥幸心理,我们知道侥幸不好不坏,这是首先要声明的,那么,我们需要具体多少侥幸,侥幸到什么程度才比较合适呢?比如考虑赢多少的时候离开最合适,输多少的时候离开最合适?下回再分析。
参考
- https://en.wikipedia.org/wiki/Gambler's_ruin
- Coad A, Frankish J, Roberts R G, et al. Growth paths and survival chances: An application of Gambler’s Ruin theory[J]. Journal of Business Venturing, 2013, 28(5): 615-632.