Python金融系列第五篇:多元线性回归和残差分析
作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
第一篇:计算股票回报率,均值和方差
第二篇:简单线性回归
第三篇:随机变量和分布
第四篇:置信区间和假设检验
第五篇:多元线性回归和残差分析
第六篇:现代投资组合理论
第七篇:市场风险
第八篇:Fama-French 多因子模型
介绍
在前某章中,我们介绍了简单的线性回归,它只有一个自变量。在本章中,我们将学习具有多个自变量的线性回归。
简单的线性回归模型以下列形式编写:
Y = α + β X + ϵ Y = \alpha + \beta X + \epsilon Y=α+βX+ϵ
具有 p 个变量的多元线性回归模型可以由下面的公式给出:
Y = α + β 1 X 1 + β 2 X 2 + β 3 X 3 + ⋯ + β p X p + ϵ Y = \alpha + \beta_{1}X_{1}+ \beta_{2}X_{2}+ \beta_{3}X_{3}+ \cdots + \beta_{p}X_{p} + \epsilon Y=α+β1X1+β2X2+β3X3+⋯+βpXp+ϵ
Python 实现
在上一章中,我们使用标普500指数来预测亚马逊股票收益率。现在我们将添加更多变量来改进模型的预测。特别是,我们将考虑亚马逊的竞争对手。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as sm
from pandas_datareader import data as pdr
import fix_yahoo_finance as yf
# Get stock prices
spy_table = pdr.get_data_yahoo("SPY")
amzn_table = pdr.get_data_yahoo("AMZN")
ebay_table = pdr.get_data_yahoo("EBAY")
wal_table = pdr.get_data_yahoo("WMT")
aapl_table = pdr.get_data_yahoo("AAPL")
然后我们从 2016 年开始获取收盘价:
spy = spy_table .loc['2016',['Close']]
amzn = amzn_table.loc['2016',['Close']]
ebay = ebay_table.loc['2016',['Close']]
wal = wal_table .loc['2016',['Close']]
aapl = aapl_table.loc['2016',['Close']]
在获取每个股票的日志返回后,我们将它们连接成一个 DataFrame,并打印出最后五行:
spy_log = np.log(spy.Close) .diff().dropna()
amzn_log = np.log(amzn.Close).diff().dropna()
ebay_log = np.log(ebay.Close).diff().dropna()
wal_log = np.log(wal.Close) .diff().dropna()
aapl_log = np.log(aapl.Close).diff().dropna()
df = pd.concat([spy_log,amzn_log,ebay_log,wal_log,aapl_log],axis = 1).dropna()
df.columns = ['SPY', 'AMZN', 'EBAY', 'WAL', 'AAPL']
df.tail()
| SPY | AMZN | EBAY | WAL | AAPL | |
|---|---|---|---|---|---|
| Date | |||||
| 2016-12-23 | 0.001463 | -0.007531 | 0.008427 | -0.000719 | 0.001976 |
| 2016-12-27 | 0.002478 | 0.014113 | 0.014993 | 0.002298 | 0.006331 |
| 2016-12-28 | -0.008299 | 0.000946 | -0.007635 | -0.005611 | -0.004273 |
| 2016-12-29 | -0.000223 | -0.009081 | -0.001000 | -0.000722 | -0.000257 |
| 2016-12-30 | -0.003662 | -0.020172 | -0.009720 | -0.002023 | -0.007826 |
跟以前一样,我们使用 statsmodels 包来执行简单的线性回归:
import statsmodels.formula.api as sm
simple = sm.ols(formula = 'amzn ~ spy',data = df).fit()
print(simple.summary())
OLS Regression Results
==============================================================================
Dep. Variable: amzn R-squared: 0.230
Model: OLS Adj. R-squared: 0.227
Method: Least Squares F-statistic: 74.46
Date: Tue, 09 Oct 2018 Prob (F-statistic): 7.44e-16
Time: 11:55:12 Log-Likelihood: 680.94
No. Observations: 251 AIC: -1358.
Df Residuals: 249 BIC: -1351.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0002 0.001 0.196 0.845 -0.002 0.002
spy 1.0661 0.124 8.629 0.000 0.823 1.309
==============================================================================
Omnibus: 67.332 Durbin-Watson: 2.018
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2026.389
Skew: -0.074 Prob(JB): 0.00
Kurtosis: 16.919 Cond. No. 121.
==============================================================================
同样,我们可以构建一个多元线性回归模型:
import statsmodels.formula.api as sm
model = sm.ols(formula = 'amzn ~ spy + ebay + wal',data = df).fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: amzn R-squared: 0.250
Model: OLS Adj. R-squared: 0.238
Method: Least Squares F-statistic: 20.52
Date: Tue, 09 Oct 2018 Prob (F-statistic): 1.32e-14
Time: 13:23:15 Log-Likelihood: 684.25
No. Observations: 251 AIC: -1358.
Df Residuals: 246 BIC: -1341.
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0002 0.001 0.229 0.819 -0.002 0.002
spy 1.0254 0.170 6.038 0.000 0.691 1.360
ebay -0.0774 0.058 -1.325 0.186 -0.193 0.038
wal -0.0838 0.089 -0.943 0.346 -0.259 0.091
aapl 0.1576 0.084 1.883 0.061 -0.007 0.322
==============================================================================
Omnibus: 69.077 Durbin-Watson: 1.983
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1890.930
Skew: -0.272 Prob(JB): 0.00
Kurtosis: 16.435 Cond. No. 179.
==============================================================================
从上表中我们可以看出,ebay,walmart 和 apple 的 p 值分别是 0.186,0.346,0.061,因此在 95% 置信水平下他们都不显著。多元回归模型具有比简单模型更高的 R 2 R^{2} R2 ,0.254 VS 0.234。实际上, R 2 R^{2} R2 不会随着变量数量的增加而减少。为什么呢?如果在我们的回归模型中添加一个额外的变量,但它无法解释响应中的变化(amzn),那么它的估计系数将只是零。就好像该变量从未包含在模型中一样,因此 R 2 R^{2} R2 不会改变。但是,添加数百个变量并不总是更好,这个问题我们会在后续章节中讨论。
我们可以进一步改进模型吗?在这里,我们尝试 Fama-French 5因子模型,这是资产定价理论中的一个重要模型。我们将会在后面的教程中介绍。数据下载地址
path = './F-F_Research_Data_5_Factors_2x3_daily.CSV'
fama_table = pd.read_csv(path)
# Convert time column into index
fama_table.index = [datetime.strptime(str(x), "%Y%m%d")
for x in fama_table.iloc[:,0]]
# Remove time column
fama_table = fama_table.iloc[:,1:]
通过这些数据,我们可以构建一个 Fama-French 因子模型:
fama = fama_table['2016']
fama = fama.rename(columns = {'Mkt-RF':'MKT'})
fama = fama.apply(lambda x: x/100)
fama_df = pd.concat([fama, amzn_log], axis = 1)
fama_model = sm.ols(formula = 'Close~MKT+SMB+HML+RMW+CMA', data = fama_df).fit()
print(fama_model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Close R-squared: 0.387
Model: OLS Adj. R-squared: 0.375
Method: Least Squares F-statistic: 30.96
Date: Tue, 09 Oct 2018 Prob (F-statistic): 2.24e-24
Time: 13:46:31 Log-Likelihood: 709.57
No. Observations: 251 AIC: -1407.
Df Residuals: 245 BIC: -1386.
Df Model: 5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0010 0.001 1.027 0.305 -0.001 0.003
MKT 0.9614 0.125 7.692 0.000 0.715 1.208
SMB -0.5891 0.182 -3.235 0.001 -0.948 -0.230
HML -0.1342 0.211 -0.636 0.525 -0.550 0.282
RMW -0.4852 0.264 -1.840 0.067 -1.005 0.034
CMA -1.5543 0.324 -4.797 0.000 -2.193 -0.916
==============================================================================
Omnibus: 69.466 Durbin-Watson: 1.937
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2013.541
Skew: 0.241 Prob(JB): 0.00
Kurtosis: 16.867 Cond. No. 399.
==============================================================================
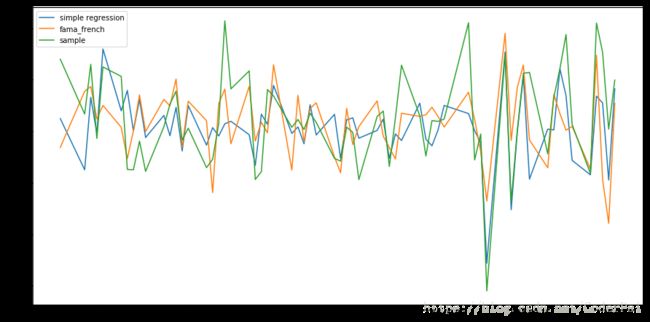
Fama-French 5因子模型的 R 2 R^2 R2 值更高,为 0.387。我们可以将简单线性回归和 Fama-French 多元回归的预测进行比较,将它们绘制在一个图表上:
result = pd.DataFrame({'simple regression': simple.predict(),
'fama_french': fama_model.predict(),
'sample': df.amzn}, index = df.index)
# Feel free to adjust the chart size
plt.figure(figsize = (15,7.5))
plt.plot(result['2016-7':'2016-9'].index,result.loc['2016-7':'2016-9','simple regression'])
plt.plot(result['2016-7':'2016-9'].index,result.loc['2016-7':'2016-9','fama_french'])
plt.plot(result['2016-7':'2016-9'].index,result.loc['2016-7':'2016-9','sample'])
plt.legend()
plt.show()
虽然从上图中很难看出,多元回归的预测回报更接近实际回报。通常我们不会绘制预测来确定哪个模型更好。
模型意义测试
我们可以执行假设检验:F 检验。而不是使用 R 2 R^{2} R2 来评估我们的回归模型是否适合数据。F检验的零假设和替代假设是:
H 0 : β 1 = β 2 = ⋯ = β p = 0 H_{0} : \beta_{1} = \beta_{2} = \cdots = \beta_{p} = 0 H0:β1=β2=⋯=βp=0
H 1 : A t l e a s t o n e c o e f f i c i e n t i s n o t 0 H_{1} : At least one coefficient is not 0 H1:Atleastonecoefficientisnot0
我们不会再这里详细解释 F 检验程序。你只需要了解 null 和替代假设。在 F 检验的汇总表中,‘F-statistic’ 是 F 分数,而 ‘prob (F-statistic)’ 是 p 值。在 Fama-French 模型上进行这个测试,我们得到一个 p 值为 2.21e-24,所以我们几乎可以肯定至少有一个系数不是 0。如果 p 值大于 0.05,你应该考虑用其他自变量重建模型。在简单线性回归中,F检验等效于斜率上的 t 检验,因此它们的 p 值将是相同的。
残差分析
线性回归要求预测变量和响应具有线性关系。无论预测变量 X 1 , ⋯ , X p X_{1}, \cdots , X_{p} X1,⋯,Xp 采用什么值,这个假设都保留残差平均为零。通常,它也假设残差是独立的,并且通常以相同的方差(同方差性)分布 ,因此我们可以构建预测区间。为了检查这些假设是否成立,我们需要分析残差。在统计套利中,残差分析也可用于生成信号。
常态
线性模型的残差通常具有正太分布。我们可以绘制残差密度来检查正态性:
plt.figure()
#ols.fit().model is a method to access to the residual.
fama_model.resid.plot.density()
plt.show()
从图中可以看出,残差是正太分布的。顺便说一句,残差平均值始终为零,达到机器精度:
print('Residual mean:', np.mean(fama_model.resid))
#[out]: Residual mean: -2.3133332345775173e-16
print('Residual variance:', np.var(fama_model.resid))
#[out]: Residual variance: 0.00020513219588900726
同方差(Homoskedasticity)
这个词英文太难念了,但是不难理解。这意味着残差对于 X 的所有值具有相同的方差。否则我们说 “异方差性” 被检测到。
plt.figure(figsize = (20,10))
plt.scatter(df.spy,simple.resid)
plt.axhline(0.05)
plt.axhline(-0.05)
plt.xlabel('x value')
plt.ylabel('residual')
plt.show()
从图表中可以看出,残差的方差不会随着 X 而增加。这三个异常值并没有改变我们的结论。虽然我们可以绘制残差用于简单回归,但我们不能对多元回归进行绘制,因此我们使用 statsmodels 来测试异方差性:
from statsmodels.stats import diagnostic as dia
het = dia.het_breuschpagan(fama_model.resid,fama_df[['MKT','SMB','HML','RMW','CMA']][1:])
print('p-value: ', het[-1])
#[out]:p-value of Heteroskedasticity: 0.14396983553305295
在 95% 的显著性水平上没有检测到异方差性。