FFT 快速傅里叶变换 初探
一直认为很高深的东西其实也并不很难。
以下内容部分来自qy大神的ppt,同时结合了自己的理解。但理解还不是很深,需要继续研究。
开头
首先什么是傅里叶变换:傅立叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。【摘自百度】
注意三角函数的特点!这一点要用到。OI中常用的是离散傅里叶变换,并用FFT加速卷积计算。
多项式的表示
点值表示法
给出N+1个不同的x代入A(x)的点值,这样的N+1个元素构成的集合{(x0,y0),(x1,y1),…,(xn,yn)},其中yi=A(xi),称为点值表示法。
为什么由此给定的多项式是惟一的?证明留以后解决。
系数表示法
N次多项式A(x)通常的表示方法为给出A(x)的系数{ak}称为系数表示法。
两种表示法的优缺点
定义:多项式乘法(卷积)A(x)*B(x)=C(x) Cn=∑Ak*Bn-k
则系数表示法的n次多项式A(x),B(x)可以O(n)快速求得A(x)+B(x),但是卷积通常需要O(n^2)计算
点值表示法的n次多项式卷积可以O(n)计算,只需将值域y对应相乘即可{(xi,yi)}×{(xi,zi)}={(xi,yi*zi)} (由于n项确定次数界为n的多项式,故计算卷积是至少保留2n项,注意这里)
系数与点值表示法的转化
系数表示法→点值表示法:
朴素计算O(n^3)
秦九韶算法/霍纳法则O(n^2)
点值表示法→系数表示法
高斯消元O(n^3)
拉格朗日插值法O(n^2):A(x)=∑(0<=k<=n)yk*Π(j≠k)(x-xj)/(xk-xj)
为快速转化系数点值表示法,于是引入快速傅里叶变换。
FFT
首先
我们的问题是:计算一个系数表示法的多项式在某n个值下的值。
一些定义
在复数平面上,定义主n次单位根:w^n=1,w为n次单位根(此处w是一个复数,相当于复数平面上的一个向量),由向量运算的性质,可知w一定在单位圆上,且将单位圆n等分。
定义wk=w^k,则可以发现wa*wb=w((a+b)%n),具有循环特征。
分治算法
由于有“优美”的循环性质,而且点值表示法对带入的点没有要求,于是可以分治,将这些n次单位根带入:
转化问题
令n=2^k,则问题变成求多项式A(w^(0..n-1))的值
若不等,可以添加一些系数为0的高次项,这都是细节。
分而治之
将A(x)奇偶项拆开,
令A0(x)=a0x^0+a2x^1+……+(an-2)x^(n/2-1)
A1(x)=a1x^0+a3x^1+……+(an-1)x^(n/2-1)
则有A(x)=A0(x^2)+xA1(x^2)
原始带入的是w^0,w^1,w^2,…
现在变成带入w^0,w^2,w^4,…
进行一下变换w’=w(n/2),即w’^(n/2)=1
现在变成带入w’^0,w’^1,w’^2,…
这样问题就缩小了一半
继续分治即可
合并时是O(n),总时间复杂度是O(nlogn)
逆FFT
这要涉及范德蒙矩阵的相关知识,暂不说明。
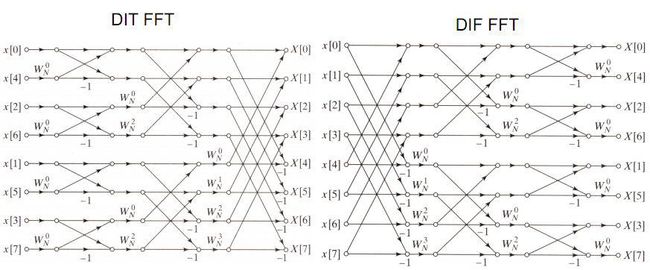
图解(引用)
【据说像蝴蝶,然而?】
实现
由于分治方法常数较大,故在实际使用中通常使用迭代方法计算FFT。
具体方法
模拟从底层递归的过程,在原地操作变换数组。
结束语
FFT,本质也是分治算法的应用,充分利用数学知识,同时结合OI实际,才能灵活运用。
再次感谢qy大神。
参考资料
冰封寒月 讲解与PPT
百度百科