OpenCasCade与NURBS——B样条曲线

NURBS是非均匀有理B样条的简称，NURBS是现在通用CAD软件中比较高级的建模方法，B样条在创建曲线或曲面时有很高的灵活性，会用并善用基本上能获得想要的任意“自然”、光滑的曲线。
OpenCasCade是国外一款开源的CAD建模引擎，功能比较完备、强大。现在OpenCasCade母公司也以提供基于OpenCasCade的定制化CAD软件和服务为主要业务。

B样条曲线的分类

B样条曲线是B样条基曲线的线性组合。其分类包括均匀B样条、准均匀B样条、分段Bezier曲线和非均匀有理B样条曲线。在OpenCasCade中以同样的9个控制点和次数（2次）绘制对应的曲线。

1. 均匀B样条曲线

均匀B样条的节点值向量均匀分布，并且基函数呈周期性，即所有的基函数都有相同的形状。

2. 准均匀B样条曲线

与均匀B样条的区别在于两端点具有重复度，如果样条曲线的次数为k，则如果要过端点，则需要将重复度设为k+1。

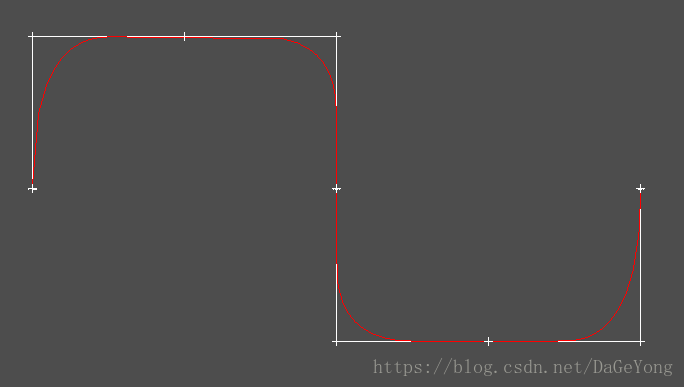
3. 分段Bezier曲线

分段Bezier曲线结合了Bezier曲线和B样条曲线的优点，即可以分段控制，又可以采用Bezier曲线的简单算法。分段Bezier曲线在插值圆弧时有很好的准确性。

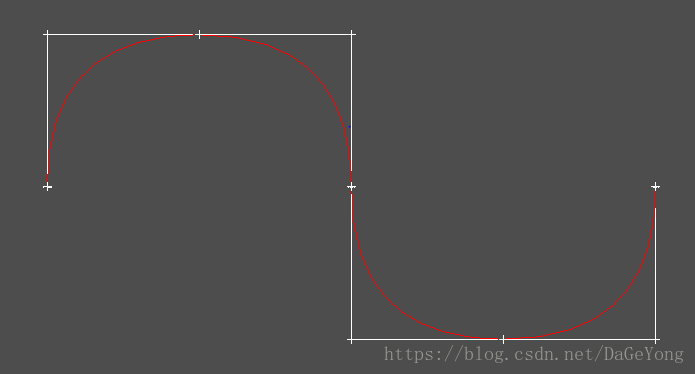
4. 非均匀有理B样条曲线

非均匀有理B样条曲线可以通过部分节点的权因子来控制曲线的局部的形状，某点的权因子越大，越靠近该点。在OCC中，与上述三种不同的是，在构造有理B样条时额外需要一个权因子列表，实际上，分段Bezier曲线也可以传入一个权因子列表来修改曲线局部的形状。

在OCC中，上述三种曲线的构造及显式对应的代码如下：

TColgp_Array1OfPnt Poles(1,9);
    Poles.SetValue(1, gp_Pnt(0,-100,0));
    Poles.SetValue(2, gp_Pnt(0,-100,50));
    Poles.SetValue(3, gp_Pnt(0,-50,50));
    Poles.SetValue(4, gp_Pnt(0,0,50));
    Poles.SetValue(5, gp_Pnt(0,0,0));
    Poles.SetValue(6, gp_Pnt(0,0,-50));
    Poles.SetValue(7, gp_Pnt(0,50,-50));
    Poles.SetValue(8, gp_Pnt(0,100,-50));
    Poles.SetValue(9, gp_Pnt(0,100,0));

    TColStd_Array1OfReal PolesWeight(1,9);
    PolesWeight.SetValue(1, 1.0);
    PolesWeight.SetValue(2, 0.707);
    PolesWeight.SetValue(3, 1.0);
    PolesWeight.SetValue(4, 0.707);
    PolesWeight.SetValue(5, 1.0);
    PolesWeight.SetValue(6, 0.707);
    PolesWeight.SetValue(7, 1.0);
    PolesWeight.SetValue(8, 0.707);
    PolesWeight.SetValue(9, 1.0);



    for(int i=0; i<9; ++i)
    {
        TopoDS_Vertex aVertex = BRepBuilderAPI_MakeVertex(Poles.Value(i+1));
        Handle(AIS_Shape) vert = new AIS_Shape(aVertex);
        myAISContext->SetColor(vert,Quantity_NOC_WHITE,Standard_False); 
        myAISContext->Display(vert,Standard_False);

        if(i != 8)
        {
            TopoDS_Edge tedge = BRepBuilderAPI_MakeEdge(Poles.Value(i+1), Poles.Value(i+2));
            TopoDS_Wire twire= BRepBuilderAPI_MakeWire(tedge);
            Handle(AIS_Shape) awire = new AIS_Shape(twire);
            myAISContext->SetColor(awire,Quantity_NOC_WHITE,Standard_False); 
            myAISContext->Display(awire, Standard_False);
        }
        Fit();
    }

    Fit();

    Standard_Integer curtype = 4;
    if(curtype == 1)
    {
        /// 均匀B样条，节点向量中的节点值成等差排布
        /// 均匀B样条的基函数呈周期性，即所有的基函数有相同的形状
        /// 每个后续基函数仅仅市前面基函数在新位置上的重复

        Standard_Integer degree(2);
        Standard_Integer PNum = 9;
        Standard_Integer KNum = PNum + degree + 1;
        TColStd_Array1OfReal knots(1,KNum);
        for(int i=0; i1, i);
        }
        TColStd_Array1OfInteger mults(1,KNum);
        for(int i=0; i1, 1);
            std::cout << mults.Value(i+1) << std::endl;
        }
        Handle(Geom_BSplineCurve) curve = new Geom_BSplineCurve(Poles, knots, mults, degree);
        TopoDS_Edge ed1 = BRepBuilderAPI_MakeEdge(curve);
        TopoDS_Wire wr1 = BRepBuilderAPI_MakeWire(ed1);

        Handle(AIS_Shape) red = new AIS_Shape(wr1);
        myAISContext->SetColor(red,Quantity_NOC_RED,Standard_False); 
        myAISContext->Display(red,Standard_False);
        Fit();

    }
    else if(curtype == 2)
    {
        /// 准均匀B样条，节点向量中的节点值也是等差排布，但是起点和终点都有k-1的重复度，其中ke为曲线次数。

        Standard_Integer degree(2);
        Standard_Integer PNum = 9;
        Standard_Integer KNum = PNum-1;
        TColStd_Array1OfReal knots(1,KNum);
        for(int i=0; i1, i);
        }
        TColStd_Array1OfInteger mults(1,KNum);
        for(int i=0; iif(i == 0 || i == KNum-1)
            {
                mults.SetValue(i+1, degree+1);
            }
            else
            {
                mults.SetValue(i+1, 1);
            }
        }
        Handle(Geom_BSplineCurve) curve = new Geom_BSplineCurve(Poles, knots, mults, degree);
        TopoDS_Edge ed1 = BRepBuilderAPI_MakeEdge(curve);
        TopoDS_Wire wr1 = BRepBuilderAPI_MakeWire(ed1);

        Handle(AIS_Shape) red = new AIS_Shape(wr1);
        myAISContext->SetColor(red,Quantity_NOC_RED,Standard_False); 
        myAISContext->Display(red,Standard_False);
        Fit();
    }
    else if(curtype == 3)
    {
        /// 分段Bezier曲线
        Standard_Integer degree(2);
        Standard_Integer PNum = 9;
        Standard_Integer KNum = PNum - 4;
        TColStd_Array1OfReal knots(1,KNum);
        for(int i=0; i1, i);
        }
        TColStd_Array1OfInteger mults(1,KNum);
        for(int i=0; iif(i == 0 || i == KNum-1)
            {
                mults.SetValue(i+1, degree+1);
            }
            else
            {
                mults.SetValue(i+1, degree);
            }
        }
        Handle(Geom_BSplineCurve) curve = new Geom_BSplineCurve(Poles, knots, mults, degree);
        TopoDS_Edge ed1 = BRepBuilderAPI_MakeEdge(curve);
        TopoDS_Wire wr1 = BRepBuilderAPI_MakeWire(ed1);

        Handle(AIS_Shape) red = new AIS_Shape(wr1);
        myAISContext->SetColor(red,Quantity_NOC_RED,Standard_False); 
        myAISContext->Display(red,Standard_False);
        Fit();
    }
    else if(curtype == 4)
    {
        /// 有理B样条曲线
        Standard_Integer degree(2);
        Standard_Integer PNum = 9;
        Standard_Integer KNum = PNum - 1;
        TColStd_Array1OfReal knots(1,KNum);
        for(int i=0; i1, i);
        }
        TColStd_Array1OfInteger mults(1,KNum);
        for(int i=0; iif(i == 0 || i == KNum-1)
            {
                mults.SetValue(i+1, degree+1);
            }
            else
            {
                mults.SetValue(i+1, 1);
            }
        }
        Handle(Geom_BSplineCurve) curve = new Geom_BSplineCurve(Poles, PolesWeight, knots, mults, degree);
        TopoDS_Edge ed1 = BRepBuilderAPI_MakeEdge(curve);
        TopoDS_Wire wr1 = BRepBuilderAPI_MakeWire(ed1);

        Handle(AIS_Shape) red = new AIS_Shape(wr1);
        myAISContext->SetColor(red,Quantity_NOC_RED,Standard_False); 
        myAISContext->Display(red,Standard_False);
        Fit();
    }

OpenCasCade，路漫漫其修远兮。