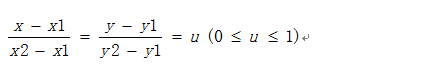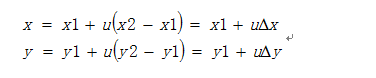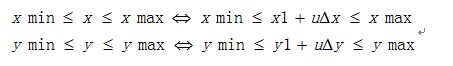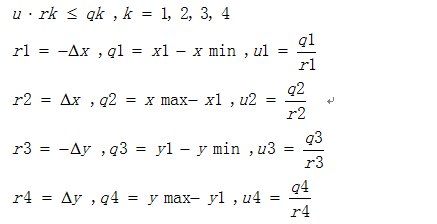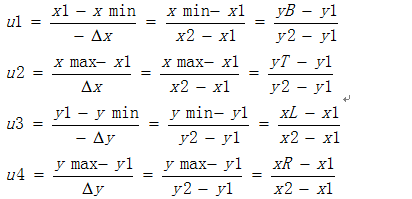理解梁友栋-Barsky裁剪算法
消除指定区域内或区域外的图形部分的过程称为裁剪。在一维裁剪窗口中<1>,线段与裁剪窗口的关系如下图所示
假设点P1P2W1W2的横坐标分别是x1,x2,w1,w2,线段P1P2与蓝色裁剪窗口W1W2(蓝色的线之间)的存在公共部分(可见部分)的充要条件是:
max(min(x1,x2), min(w1,w2))≤ min(max(x1,x2), max(w1,w2))
即所谓左端点中大者<=右端点中的小者{1}
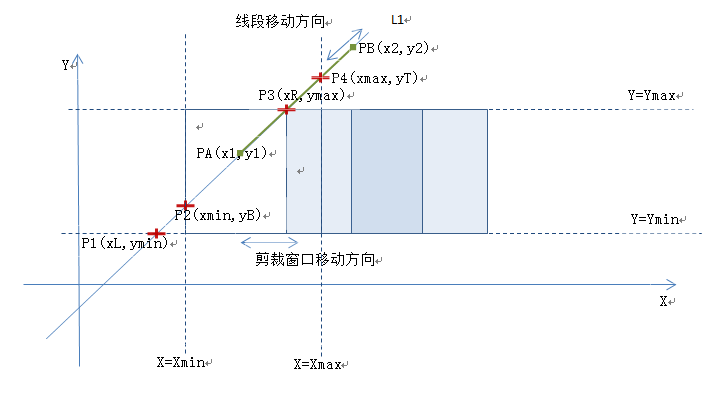
根据一维裁剪窗口与线段的左右两端点的坐标值大小,就能确定线段和裁剪窗口的可见部分,二维坐标系中计算裁剪窗口和线段的可见部分,竟然也能转化为一维裁剪就是该算法的精髓所在,方法就是计算裁剪窗口延长线与线段所在的直线的交点。二维空间中只要指定一个空间中一点和通过该点的直线的斜率(k)就能唯一确定一条直线,当直线不与坐标轴平行时,一定与裁剪窗口的边所在的两对延长线存在交点。为了了解裁剪窗口和线段交点的情形,先确定一条直线L1(k>0),和裁剪窗口的纵坐标值ymin,ymax假如所求线段PAPB在L1上沿L1上下滑动,裁剪窗口沿水平方向左右滑动,则可以完全枚举出线段与裁剪窗口所有交点的情形,如下图所示:
线段的两个端点分别是PA(x1,y1),PB(x2,y2),L1与Y=Ymin的交点P1(xL,ymin),与Y=Ymax的交点P3(xR,ymax)。当线段的一个端点PA滑动到P3之上或PB滑动到P1之下时,无论裁剪窗口怎么滑动都不可能与PAPB存在公共部分。
线段L1的参数方程(1)如下所示:
设Δx=x2-x1,Δy=y2-y1,参数u在0~1之间取值 ,任何线段上的点P(x,y)都可以满足下面的方程(2):
当点P位于由(xmin,ymin)和(xmax,ymax)所确定的裁剪窗口内时满足下面不等式(3):
上面的不等式组可以表示为4个不等式(4):
其中r1与r2符号相反,r3与r4符号相反。对于r=0的情形,表示线段PAPB平行于坐标轴,很容易确定它与裁剪窗口是否有公共部分。r不等于0的时候,对于上面四个不等式,当rk < 0时 ,u >= qk/rk,当rk>0时 u <= qk/rk,则点P才能位于裁剪窗口之内。同理,假如P已经落在了裁剪窗口之内,u一定大于等于所有rk<0对应的uk的最大值,而小于等于所有rk>0时对应的uk最小值。同时有下面的等式(5):
下面讨论线段在前面图中的PAPB与裁剪窗口的关系,显然r1 < 0 , r2 > 0 , r3 < 0 , r4 > 0,所以 u1与u3的大小关系其实就代表了xmin与xL的大小关系,xL是L1与裁剪窗口底部延长线y=ymin的交点的横坐标。u2与u4的大小关系,代表了xmax与xR的大小关系,而xR是L1与裁剪窗口顶部延长线y=ymax的交点的横坐标。根据一维裁剪窗口与线段的定理{1},若左端点大者(max(xmin,xL))小于右端点小者(min(xmax,xR))时,可以看出L1与裁剪窗口一定有公共部分,反之,PAPB在裁剪窗口之外,但是通过uk只能求出直线L1与裁剪窗口可见部分,根据梁友栋-Barsky裁剪算法rk<0求出的uk最大值是左端点的u值,按照rk>0求出的uk的最小值是右端点的u值,当线段与裁剪窗口有可见部分时u在范围[0,1]中。当r1>0,r2<0,r3>0,r4<0等剩余三种情形类似。
参考资料:
http://cg.sjtu.edu.cn/lecture_site/chap3/mainframe312.htm
http://www.cnblogs.com/jenry/archive/2012/02/12/2347983.html