CTR 预测理论（七）：LR+离散特征原因、优势及替代方案

在回顾腾讯广告算法大赛时候想到这个问题，总结整理一下这个问题。

1. LR+离散特征优势：

在工业界，很少直接将连续值作为特征喂给逻辑回归模型，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：

1. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易scalable（扩展）。

2. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰。

3. 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合。

4. 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力。

5. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；

李沐少帅指出，模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说，前者容易，而且可以n个人一起并行做，有成功经验；后者目前看很赞，能走多远还须拭目以待。

大概的理解：

1）计算简单

2）简化模型

3）增强模型的泛化能力，不易受噪声的影响

2. LR+离散特征原因

2.1 人工特征 VS 机器特征

首先，海量离散特征＋LR是业内常见的一个做法，但并不是Holy Grail，事实上这一般而言仅仅是因为LR的优化算法更加成熟，而且可以在计算中利用稀疏特性进行更好的优化—可谓不得已而为之。

事实证明GBDT和深度学习特征的加入对于CTR预测是有正面帮助的。如果这个问题思考地更深一点，其实当前深度学习网络的最后一层，如果是binary classification，其实等同于LR。所以说，通过人工／半人工的方式产生的features，跟深度神经网络（无论之前用了怎样的结构）最后学出来的representation，其实是异曲同工，区别在于深度学习一般而言会学出一个dense representation，而特征工程做出来的是一堆sparse representation。某些时候，人工特征其实跟神经网络经过几层非线性之后的结果是高度相似的。在暴力提取高阶／非线性特征的本事上，机器肯定胜过人类。但是，就算最牛的机器智能，有时候都敌不过一些“人类常识”。尤其是业务的一些逻辑，可以认为是人脑在更大的一个数据集上pre-train出来的一些特征，其包含的信息量一定是大于你用于预测的dataset的。在这种情况下，往往厉害的人工features会outperform暴力的机器方法。所以，特征离散化，从数学角度来说可以认为是增加robustness，但是更重要的，make sense of the data，将数据转变成人类可以理解、可以validate的格式。人类的业务逻辑，当然也不是完美的。在当前机器智能还未征服“常识”这个领域之前，人类的business insights还是一个有力的补充（在很多case，甚至是最重要的部分）。在机器能够完全掌握的范围内，譬如围棋，人类引以为傲的intuition已经无法抵抗机器的暴力计算了——所以在未来，我们一定会看到越来越多的机器智能开始侵入一些传统上认为必须要依靠人类的“感觉”的一些领域。广告领域当然也不能躲过这个大的趋势。

2.2 LR 适用于稀疏特征原因

这个问题我也是思考了好久，在平时的项目中也遇到了不少 case，确实高维稀疏特征的时候，使用 gbdt 很容易过拟合。

但是还是不知道为啥，后来深入思考了一下模型的特点，发现了一些有趣的地方。

假设有1w 个样本， y类别0和1，100维特征，其中10个样本都是类别1，而特征 f1的值为0，1，且刚好这10个样本的 f1特征值都为1，其余9990样本都为0(在高维稀疏的情况下这种情况很常见)，我们都知道这种情况在树模型的时候，很容易优化出含一个使用 f1为分裂节点的树直接将数据划分的很好，但是当测试的时候，却会发现效果很差，因为这个特征只是刚好偶然间跟 y拟合到了这个规律，这也是我们常说的过拟合。但是当时我还是不太懂为什么线性模型就能对这种 case 处理的好？照理说 线性模型在优化之后不也会产生这样一个式子：$y=W_1\ast f_1+\cdots +Wi\ast fi+\cdots$，其中 $W_1$特别大以拟合这十个样本吗，因为反正 f1的值只有0和1，$W_1$过大对其他9990样本不会有任何影响。

后来思考后发现原因是因为现在的模型普遍都会带着正则项，而 lr 等线性模型的正则项是对权重的惩罚，也就是 $W_1$一旦过大，惩罚就会很大，进一步压缩 $W_1$的值，使他不至于过大，而树模型则不一样，树模型的惩罚项通常为叶子节点数和深度等，而我们都知道，对于上面这种 case，树只需要一个节点就可以完美分割9990和10个样本，惩罚项极其之小。

这也就是为什么在高维稀疏特征的时候，线性模型会比非线性模型好的原因了：带正则化的线性模型比较不容易对稀疏特征过拟合。

2.3 为什么LR只适合离散特征

LR是一个非常简单的线性模型。 我们再次回顾它的公式：y = w*x + b。 这是一个线性函数。 我们之前说0过， 线性函数的表达能力有限， 我们引入激活函数就是为了给LR增加非线性关系。能让一条直线变成曲线。这样可以拟合出更好的效果。（也由此才后了后来说的过拟合问题而引入了正则化超参数）， 那么离散化和连续化最大的区别是，对一个字段做连续化后的结果就还只是一个特征，而离散化后的这一列有多少个key(字段可能的值)就会抽取出多少个特征。 那么第一点就来了， 单变量离散化为N个后，每个变量有单独的权重，在激活函数的作用下相当于为模型增加了非线性，能够提升模型表达能力，加大拟合。 第二点，离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰， 因为特征值的异常会导致权重也就是w的值也会异常。第三，离散特征的增加和减少都很容易，易于模型的快速迭代。 第四， 一定有同学担心特征过多会导致运算缓慢，但是LR是线性模型， 我们在内部计算的时候是向量化计算，而不是循环迭代。稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展。 所以不用担心像GBDT算法那样，特征多了就跑不动了(我们都说GBDT不能用离散特征不是因为它处理不了离散特征，而是因为离散化特征后会产生特别多的特征，决策树的叶子节点过多，遍历的时候太慢了)。 所以海量离散特征＋LR是业内常见的一个做法。而少量连续特征+复杂模型是另外一种做法，例如GBDT。

2.4 连续和离散的相互转化

这回我们知道了离散和连续的区别，以及他们的应用场景。但数据并不是我们随随便便想离散就离散想连续就连续的。假如你想给资产这个字段做离散化， 每个key都是一个特征，那么就会有海量的特征出现，1000和1001以及999变成了3个不同的特征， 这可不是我们想要的，中间差那么一块钱很重要么？ 我们更希望的是在某一个区间内的数字统一映射成一个特征。 例如资产100w以下的算穷人特征，100w到1000W算中产特征，1000W以上的算富人特征。可能这才是我们想要从这个字段中提取出的3个特征。所以才有了连续值分桶方法来把连续特征转换成离散特征。把连续特征的区间分成不同的桶进行转化。 同样的离散特征也可以转换成连续特征，可能的做法是把数据按时间字段进行排序，然后根据时间窗口的数据的值把离散的数据转化成一个数字的值。 具体的细节我也不是很清楚。大家可以查查资料。

2.4 归一化

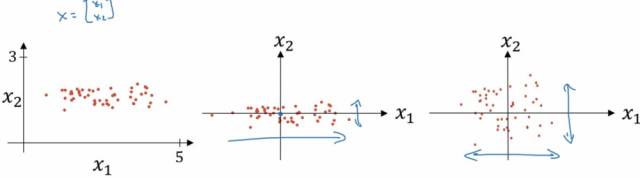
归一化也是一个满重要的步骤。 在我们提取出特征后，我们发现这些特征的值得区间是不一样的。尤其对于连续特征。 特征一的区间是 0 ~ 1， 特征二的区间是0 ~ 1000,。那么我们做梯度下降就如下图：

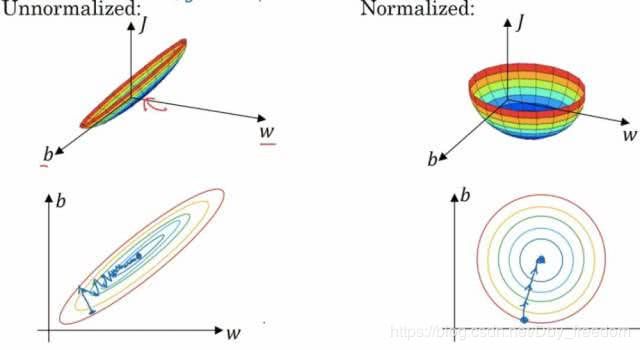
左边是未经过归一化的图，这时候的梯度下降算法有点像一个扁平的碗， 这时候我们需要更多的迭代次数来完成梯度下降。 而右边是经过了归一化的梯度下降，是一个更圆润的碗，我们会更快的进行梯度下降。 那么到底什么是归一化呢， 其实归一化就是把我们的特征值压缩成0~1的区间，让所有的特征都处于一个相对平等的状态。如下图：

本来特征是在最左边这样分布的，通过归一化，特征的分布慢慢的就变成了最右边的样子。 所以在我们的特征处于不同的分布区间的时候，归一化很有用。 我们在深度学习中，也会有batch norm的操作。其实就是把每一层的输出都进行归一化处理后再交给下一层计算。

3. GBDT编码， LR建模

用LR做点击率预估时，需要做大量的特征工程。将连续特征离散化，并对离散化的特征进行One-Hot编码，最后对特征进行二阶或者三阶的特征组合，目的是为了得到非线性的特征。特征工程存在几个难题：

• 连续变量切分点如何选取？
• 离散化为多少份合理？
• 选择哪些特征交叉？
• 多少阶交叉，二阶，三阶或更多？

一般都是按照经验，不断尝试一些组合，然后根据线下评估选适当参数。

但是，使用GBDT编码，一举解决了上面的问题。确定切分点不在是凭主观经验，而是根据信息增益，客观的选取切分点和份数。每棵决策树从根节点到叶节点的路径，会经过不同的特征，此路径就是特征组合，而且包含了二阶，三阶甚至更多。

为什么不直接用GDBT，而非要用GDBT+LR呢？因为GDBT在线预测比较困难，而且训练时间复杂度高于LR。所以实际中，可以离线训练GDBT，然后将该模型作为在线ETL的一部分。

虽然Facebook论文提到GBDT+LR的效果是好于纯GBDT，甚至LR的性能也比GBDT要好。其实，我存怀疑态度的，所以我用 R 在本地做了一个实验，数据源是mlbench的5个数据包diabetes，satellite，sonar，vehicle和vowel，除了召回率指标，其他所有指标均是gbdt > gbdt + lr > lr，这一点符合我之前的设想。

当然，我的数据集也比较有限，不能以偏概全。但是从实验数据来看，这些算法在各项指标没有质的区别，所以实际工作中，找到重要的特征才是头等大事；算法方面，选择能够快速上线，够用就行，后面可以迭代优化。

其他命题纪要：

下面简单记录论文其他方面的主题，方便后面回顾

• 梯度下降学习率更新策略，本文介绍了常见的几种，并给出的试验数据
• 在线学习中，LR对BOPR。BOPR效果稍微好于LR，但是LR更为简单，所以最后还是选择了LR
• GDBT迭代轮数，大部分优化只需要500轮迭代GBDT模型可以完成。
• GDBT的数深度也不需要太深，2,3层一般满足要求。
• 特征也不是越多越好，重要性前Top 400特征就可以表现很好
• 历史特征比用户当前上下文特征更为重要，而且对预测的时间更为稳定。但是用户上下文数据可以有效的解决冷启动问题。
• 无需使用全部的样本，使用10%的训练数据的效果与100%没有太大差别
• 如果对负样本重采样，模型计算的概率，需要重新修正。修正公式为q=pp+(1−p)/w，其中q是修正后的数据，p时模型预测的数据，w是负样本重采样比例。

参考文献

[1] 连续特征的离散化：在什么情况下将连续的特征离散化之后可以获得更好的效果？
[2] GBDT 特征转换 + LR 总结
[3] 深度学习基础（七）-特征工程
[4] 逻辑回归LR的特征为什么要先离散化