CTR预估 论文精读(七)--DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
Abstract
Learning sophisticated feature interactions behind user behaviors is critical in maximizing CTR for recommender systems. Despite great progress, existing methods seem to have a strong bias towards low- or high-order interactions, or require expertise feature engineering. In this paper, we show that it is possible to derive an end-to-end learning model that emphasizes both low- and highorder feature interactions. The proposed model, DeepFM, combines the power of factorization machines for recommendation and deep learning for feature learning in a new neural network architecture. Compared to the latest Wide & Deep model from Google, DeepFM has a shared input to its “wide” and “deep” parts, with no need of feature engineering besides raw features. Comprehensive experiments are conducted to demonstrate the effectiveness and efficiency of DeepFM over the existing models for CTR prediction, on both benchmark data and commercial data.
1. CTR预估
CTR预估数据特点:
- 输入中包含类别型和连续型数据。类别型数据需要one-hot,连续型数据可以先离散化再one-hot,也可以直接保留原值
- 维度非常高
- 数据非常稀疏
- 特征按照Field分组
CTR预估重点在于学习组合特征。注意,组合特征包括二阶、三阶甚至更高阶的,阶数越高越复杂,越不容易学习。Google的论文研究得出结论:高阶和低阶的组合特征都非常重要,同时学习到这两种组合特征的性能要比只考虑其中一种的性能要好。
那么关键问题转化成:如何高效的提取这些组合特征。一种办法就是引入领域知识人工进行特征工程。这样做的弊端是高阶组合特征非常难提取,会耗费极大的人力。而且,有些组合特征是隐藏在数据中的,即使是专家也不一定能提取出来,比如著名的“尿布与啤酒”问题。
在DeepFM提出之前,已有LR,FM,FFM,FNN,PNN(以及三种变体:IPNN,OPNN,PNN*),Wide&Deep模型,这些模型在CTR或者是推荐系统中被广泛使用。
2. 模型演进历史
DeepFM借鉴了Google的wide & deep的做法,其本质是
- 将Wide & Deep 部分的wide部分由 人工特征工程+LR 转换为FM模型,避开了人工特征工程;
- FM模型与deep part共享feature embedding。
2.1 线性模型
最开始CTR或者是推荐系统领域,一些线性模型取得了不错的效果。比如:LR,FTRL。线性模型有个致命的缺点:无法提取高阶的组合特征。所以常用的做法是人为的加入pairwise feature interactions。即使是这样:对于那些出现很少或者没有出现的组合特征以及高阶组合特征依旧无法提取。
LR最大的缺点就是无法组合特征,依赖于人工的特征组合,这也直接使得它表达能力受限,基本上只能处理线性可分或近似线性可分的问题。
2.2 FM模型
线性模型差强人意,直接导致了FM模型应运而生(在Kaggle上打比赛提出来的,取得了第一名的成绩)。FM通过隐向量latent vector做内积来表示组合特征,从理论上解决了低阶和高阶组合特征提取的问题。但是实际应用中受限于计算复杂度,一般也就只考虑到2阶交叉特征。
后面又进行了改进,提出了FFM,增加了Field的概念。
2.3 遇上深度学习
随着DNN在图像、语音、NLP等领域取得突破,人们见见意识到DNN在特征表示上的天然优势。相继提出了使用CNN或RNN来做CTR预估的模型。但是,CNN模型的缺点是:偏向于学习相邻特征的组合特征。 RNN模型的缺点是:比较适用于有序列(时序)关系的数据。
FNN (Factorization-machine supported Neural Network) 的提出,应该算是一次非常不错的尝试:先使用预先训练好的FM,得到隐向量,然后作为DNN的输入来训练模型。缺点在于:受限于FM预训练的效果。
随后提出了PNN (Product-based Neural Network),PNN为了捕获高阶组合特征,在embedding layer和first hidden layer之间增加了一个product layer。根据product layer使用内积、外积、混合分别衍生出IPNN, OPNN, PNN*三种类型。
无论是FNN还是PNN,他们都有一个绕不过去的缺点:**对于低阶的组合特征,学习到的比较少。**而前面我们说过,低阶特征对于CTR也是非常重要的。
Google意识到了这个问题,为了同时学习低阶和高阶组合特征,提出了Wide&Deep模型。它混合了一个线性模型(Wide part)和Deep模型(Deep part)。这两部分模型需要不同的输入,而Wide part部分的输入,依旧依赖人工特征工程。
但是,这些模型普遍都存在两个问题:
- 偏向于提取低阶或者高阶的组合特征。不能同时提取这两种类型的特征。
- 需要专业的领域知识来做特征工程。
DeepFM在Wide&Deep的基础上进行改进,成功解决了这两个问题,并做了一些改进,其优势/优点如下:
- 不需要预训练FM得到隐向量
- 不需要人工特征工程
- 能同时学习低阶和高阶的组合特征
- FM模块和Deep模块共享Feature Embedding部分,可以更快的训练,以及更精确的训练学习
3. DeepFM
DeepFM闪亮登场!
主要做法如下:
- FM Component + Deep Component。FM提取低阶组合特征,Deep提取高阶组合特征。但是和Wide&Deep不同的是,DeepFM是端到端的训练,不需要人工特征工程。
- 共享feature embedding。FM和Deep共享输入和
feature embedding不但使得训练更快,而且使得训练更加准确。相比之下,Wide&Deep中,input vector非常大,里面包含了大量的人工设计的pairwise组合特征,增加了他的计算复杂度。
DeepFM架构图:
Figure 1: Wide & deep architecture of DeepFM. The wide and deep component share the same input raw feature vector, which enables DeepFM to learn low- and high-order feature interactions simultaneously from the input raw features.
3.1 FM Component
FM部分的输出由两部分组成:一个Addition Unit,多个内积单元。
y F M = < w , x > + ∑ j 1 = 1 d ∑ j 2 = j 1 + 1 d < V i , V j > x j 1 ⋅ x j 2 y_{FM} = <w,x> + \sum_{j_1 = 1}^{d} \sum_{j_2 = j_1 + 1}^{d} <V_i, V_j>x_{j_1} \cdot x_{j_2} yFM=<w,x>+j1=1∑dj2=j1+1∑d<Vi,Vj>xj1⋅xj2
这里的d是输入one-hot之后的维度,我们一般称之为feature_size。对应的是one-hot之前的特征维度,我们称之为field_size。
FM架构图:
Figure 3: The architecture of DNN
Addition Unit 反映的是1阶的特征。内积单元反映的是2阶的组合特征对于预测结果的影响。
注意:
虽然公式上Y_fm是所有部分都求和,是一个标量。但是从FM模块的架构图上我们可以看到,输入到输出单元的部分并不是一个标量,应该是一个向量。
实际实现中采用的是FM化简之后的内积公式,最终的维度是:field_size + embedding_size(对应FM Layer中的神经元个数: Field数量 + 嵌入维度 = F + k,其中 F 为one-hot之前特征维度,k 为embedding的特征维度)
这里分别展开解释下维度的两部分是怎么来的,对于理解模型还是很重要的:
-
field_size对应的是这里的X是one-hot之后的,one-hot之后,我们认为X的每一列都是一个单独的维度的特征。这里我们表达的是X的1阶特征,说白了就是单独考虑X的每个特征,他们对最终预测的影响是多少。是多少那?是W!W对应的就是这些维度特征的权重。假设one-hot之后特征数量是
feature_size,那么W的维度就是(feature_size, 1)。这里
这里解释下Embedding: W是一个矩阵,每一行对应X的一个维度的特征(这里是one-hot之后的维度,一定要注意)。W的列数为1,表示嵌入之后的维度是1。W的每一行对应一个特征,相当于是我们拿输入X_i作为一个index, X_i的任意一个Field i中只有1个为1,其余的都是0。哪个位置的特征值为1,那么就选中W中对应的行,作为嵌入后这个Field i对应的新的特征表示。对于每一个Field都执行这样的操作,就选出来了X_i Embedding之后的表示。注意到,每个Field都肯定会选出且仅选出W中的某一行(想想为什么?),因为W的列数是固定的,每一个Field都选出W.cols作为对应的新特征。把每个Field选出来的这些W的行,拼接起来就得到了X Embedding后的新的表示:维度是
num(Field) * num(W.cols)。虽然每个Field的长度可能不同,但是都是在W中选择一行,所以选出来的长度是相同的。这也是Embedding的一个特性:虽然输入的Field长度不同,但是Embedding之后的长度是相同的。什么?Embedding这么复杂,怎么实现的?**非常简单!直接把X和W做内积即可。**是的,你没看错,就是这么简单(tensoflow中封装了下,改成了
tf.nn.embedding_lookup(embeddings, index),原理就是不做乘法,直接选出对应的行)。自己写个例子试试:X.shape=(1, feature_size), W.shape = (feture_size, embedding_size)就知道为什么选出1对应W的行和做内积结果是一样的是怎么回事了。所以:**FM模块图中,黑线部分是一个全连接!W就是里面的权重。**把输入X和W相乘就得到了输出。至于
Addition Unit,我们就不纠结了,这里并没有做什么加法,就把他当成是反应1阶特征对输出的影响就行了。 -
embedding_sizeembedding_size对应的是
∑ j 1 = 1 d ∑ j 2 = j 1 + 1 d < V i , V j > x j 1 ⋅ x j 2 \sum_{j_1 = 1}^{d} \sum_{j_2 = j_1 + 1}^{d} <V_i, V_j>x_{j_1} \cdot x_{j_2} j1=1∑dj2=j1+1∑d<Vi,Vj>xj1⋅xj2FM论文中给出了化简后的公式:
∑ i = 1 n ∑ j = i + 1 n ⟨ v i , v j ⟩ x i x j ( 1 ) = 1 2 ∑ i = 1 n ∑ j = 1 n ⟨ v i , v j ⟩ x i x j − 1 2 ∑ i = 1 n ⟨ v i , v i ⟩ x i x i ( 2 ) = 1 2 ( ∑ i = 1 n ∑ j = 1 n ∑ f = 1 k v i , f v j , f x i x j − ∑ i = 1 n ∑ f = 1 k v i , f v i , f x i x i ) ( 3 ) = 1 2 ∑ f = 1 k ⟮ ( ∑ i = 1 n v i , f x i ) ⋅ ( ∑ j = 1 n v j , f x j ) − ∑ i = 1 n v i , f 2 x i 2 ⟯ ( 4 ) = 1 2 ∑ f = 1 k ⟮ ( ∑ i = 1 n v i , f x i ) 2 − ∑ i = 1 n v i , f 2 x i 2 ⟯ \sum_{i=1}^{n} \sum_{j=i+1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_j \rangle} x_i x_j \qquad\qquad\qquad\qquad\qquad\qquad(1)\\ = \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_j \rangle} x_i x_j - \frac{1}{2} \sum_{i=1}^{n} {\langle \mathbf{v}_i, \mathbf{v}_i \rangle} x_i x_i \qquad\qquad\;\;(2)\\ = \frac{1}{2} \left(\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{f=1}^{k} v_{i,f} v_{j,f} x_i x_j - \sum_{i=1}^{n} \sum_{f=1}^{k} v_{i,f} v_{i,f} x_i x_i \right) \qquad\,(3) \\ = \frac{1}{2} \sum_{f=1}^{k} {\left \lgroup \left(\sum_{i=1}^{n} v_{i,f} x_i \right) \cdot \left(\sum_{j=1}^{n} v_{j,f} x_j \right) - \sum_{i=1}^{n} v_{i,f}^2 x_i^2 \right \rgroup} \quad\;\;\,(4) \\ = \frac{1}{2} \sum_{f=1}^{k} {\left \lgroup \left(\sum_{i=1}^{n} v_{i,f} x_i \right)^2 - \sum_{i=1}^{n} v_{i,f}^2 x_i^2\right \rgroup} \qquad\qquad\qquad\;\; i=1∑nj=i+1∑n⟨vi,vj⟩xixj(1)=21i=1∑nj=1∑n⟨vi,vj⟩xixj−21i=1∑n⟨vi,vi⟩xixi(2)=21⎝⎛i=1∑nj=1∑nf=1∑kvi,fvj,fxixj−i=1∑nf=1∑kvi,fvi,fxixi⎠⎞(3)=21f=1∑k⎩⎪⎪⎪⎪⎧(i=1∑nvi,fxi)⋅(j=1∑nvj,fxj)−i=1∑nvi,f2xi2⎭⎪⎪⎪⎪⎫(4)=21f=1∑k⎩⎪⎪⎪⎪⎪⎧(i=1∑nvi,fxi)2−i=1∑nvi,f2xi2⎭⎪⎪⎪⎪⎪⎫
这里最后的结果中是在[1,K]上的一个求和。 K就是W的列数,就是Embedding后的维度,也就是embedding_size。也就是说,在DeepFM的FM模块中,最后没有对结果从[1,K]进行求和。而是把这K个数拼接起来形成了一个K维度的向量。
FM Component总结:
- FM模块实现了对于1阶和2阶组合特征的建模。
- 没有使用预训练
- 没有人工特征工程
- embedding矩阵的大小是:特征数量 * 嵌入维度。 然后用一个index表示选择了哪个特征。
需要训练的有两部分:
- input_vector和Addition Unit相连的全连接层,也就是1阶的Embedding矩阵。
- Sparse Feature到Dense Embedding的Embedding矩阵,中间也是全连接的,要训练的是中间的权重矩阵,这个权重矩阵也就是隐向量V。
3.2 Deep Component
Deep Component架构图:
Figure 3: The architecture of DNN.
Deep Component是用来学习高阶组合特征的。网络里面黑色的线是全连接层,参数需要神经网络去学习。
由于CTR或推荐系统的数据one-hot之后特别稀疏,如果直接放入到DNN中,参数非常多,我们没有这么多的数据去训练这样一个网络。所以增加了一个Embedding层,用于降低纬度。
这里继续补充下Embedding层,两个特点:
- 尽管输入的长度不同,但是映射后长度都是相同的.
embedding_size(k) - embedding层的参数其实是全连接的Weights,是通过神经网络自己学习到的。
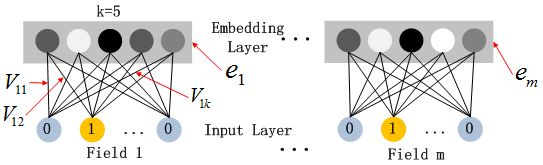
Embedding层的架构图:
embedding layer表示为:
a ( 0 ) = [ e 1 , e 2 , … , e m ] a^{(0)} = [e_1, e_2, \dots, e_m] a(0)=[e1,e2,…,em]
其中 e i e_i ei 是第 i i i 个filed的embedding,m是filed数量;
然后 a ( 0 ) a^{(0)} a(0) 传递给deep part,前馈过程如下:
a ( l + 1 ) = σ ( W ( l ) a ( l ) + b ( l ) ) a^{(l+1)} = \sigma(W^{(l)}a^{(l)} + b^{(l)}) a(l+1)=σ(W(l)a(l)+b(l))
其中 l l l 是层深度, σ \sigma σ 是激活函数, a ( l ) a^{(l)} a(l), W ( l ) W^{(l)} W(l), b ( l ) b^{(l)} b(l) 分别是第 l l l 层的输出,权重和偏置。
然后得到dense real-value 特征矢量,最后被送到sigmoid函数做CTR预测:
y D N N = σ ( W ∣ H ∣ + 1 ⋅ a ∣ H ∣ + b ∣ H ∣ + 1 ) y_{DNN} = \sigma(W^{|H|+1} \cdot a^{|H|} + b^{|H|+1}) yDNN=σ(W∣H∣+1⋅a∣H∣+b∣H∣+1)
其中 ∣ H ∣ |H| ∣H∣ 是隐藏层层数
值得注意的是:FM模块和Deep模块是共享feature embedding的(也就是V)。
好处:
- 模型可以从最原始的特征中,同时学习低阶和高阶组合特征
- 不再需要人工特征工程。Wide&Deep中低阶组合特征就是同过特征工程得到的。
3.3 对比其他模型
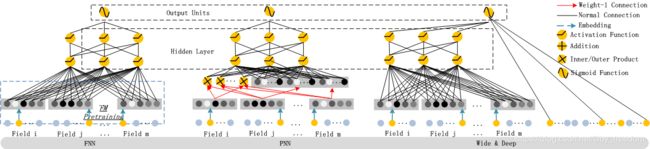
模型图:
Figure 5: The architectures of existing deep models for CTR prediction: FNN, PNN, Wide & Deep Model
3.3.1 FNN
FNN is a FM-initialized feedforward neural network.
FNN使用预训练的FM来初始化DNN,然后只有Deep部分,不能学习低阶组合特征。
FNN缺点:
- Embedding的参数受FM的影响,不一定准确
- 预训练阶段增加了计算复杂度,训练效率低
- FNN只能学习到高阶的组合特征。模型中没有对低阶特征建模。
3.3.2 PNN
PNN:为了捕获高阶特征。PNN在第一个隐藏层和embedding层之间,增加了一个product layer。
根据product的不同,衍生出三种PNN:IPNN,OPNN,PNN* 分别对应内积、外积、两者混合。
作者为了加快计算,采用近似计算的方法来计算内积和外积。内积:忽略一些神经元。外积:把m*k维的vector转换成k维度的vector。由于外积丢失了较多信息,所以一般没有内积稳定。
但是内积的计算复杂度依旧非常高,原因是:product layer的输出是要和第一个隐藏层进行全连接的。
PNN缺点:
- 内积外积计算复杂度高。采用近似计算的方法外积没有内积稳定。
- product layer的输出需要与第一个隐藏层全连接,导致计算复杂度居高不下
- 和FNN一样,只能学习到高阶的特征组合。没有对于1阶和2阶特征进行建模。
3.3.3 Wide&Deep
Wide & Deep设计的初衷是想同时学习低阶和高阶组合特征,但是wide部分需要领域知识进行特征工程。
Wide部分可以用LR来替换,这样的话就和DeepFM差不多了。
但是DeepFM共享feature embedding 这个特性使得在反向传播的时候,模型学习feature embedding,而后又会在前向传播的时候影响低阶和高阶特征的学习,这使得学习更加的准确。
Wide&Deep缺点:
- 需要特征工程提取低阶组合特征
Note:
事实上,论文已经明确指出了DeepFM相对于 Wide & Deep 的创新点:
- 将Wide & Deep 部分的wide部分由 人工特征工程+LR 转换为FM模型,避开了人工特征工程;
- FM模型与deep part共享feature embedding。
并且之处共享feature embedding,使得embedding特征得到了很好的表征,建模能力更精细。
3.3.4 DeepFM
优点:
- 没有用FM去预训练隐向量V,并用V去初始化神经网络。(相比之下FNN就需要预训练FM来初始化DNN)
- FM模块不是独立的,是跟整个模型一起训练学习得到的。(相比之下Wide&Deep中的Wide和Deep部分是没有共享的)
- 不需要特征工程。(相比之下Wide&Deep中的Wide部分需要特征工程)
- 训练效率高。(相比PNN没有那么多参数)
总结就是:
- 没有预训练(no pre-training)
- 共享Feature Embedding,没有特征工程(no feature engineering)
- 同时学习低阶和高阶组合特征(capture both low-high-order interaction features)
以上模型对比图如下:
4. 实验
4.1 实验准备
4.1.1 数据集
-
Criteo Dataset
-
Company* Dataset
4.1.2 评估指标
-
AUC (Area Under ROC)
-
Logloss (cross entropy).
4.1.3 模型比较
一共比较9个模型:LR, FM, FNN, PNN (three variants), Wide & Deep, and DeepFM
其中为了避开 Wide & Deep模型中wide部分的特征工程工作,利用LR & DNN and FM & DNN进行代替。
4.1.4 参数设置
To evaluate the models on Criteo dataset, we follow the parameter settings in [Qu et al., 2016] for FNN and PNN:
(1)dropout: 0.5;
(2) network structure: 400-400-400;
(3) optimizer: Adam;
(4) activation function: tanh for IPNN, relu for
other deep models.
To be fair, our proposed DeepFM uses the same setting. The optimizers of LR and FM are FTRL and Adam respectively, and the latent dimension of FM is 10.
4.1.5 表现评估
Efficiency Comparison
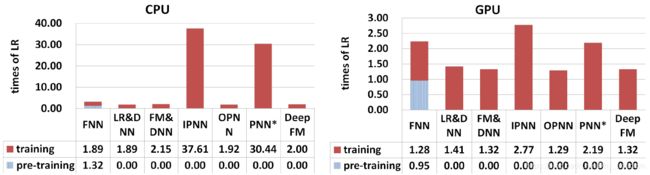
We compare the efficiency of different models on Criteo dataset by the following formula:
t r a i n i n g t i m e o f d e e p C T R m o d e l t r a i n i n g t i m e o f L R \frac{training\ time \ of \ deep \ CTR model}{training \ time \ of \ LR} training time of LRtraining time of deep CTRmodel
Figure 6: Time comparison.
DeepFM在两个数据集上几乎达到了最好的表现。
-
pre-training of FNN makes it less efficient;
-
Although the speed up of IPNN and PNN* on GPU is higher than the other models, they are still computationally expensive because of the inefficient inner product operations;
-
The DeepFM achieves almost the most efficient in both tests.
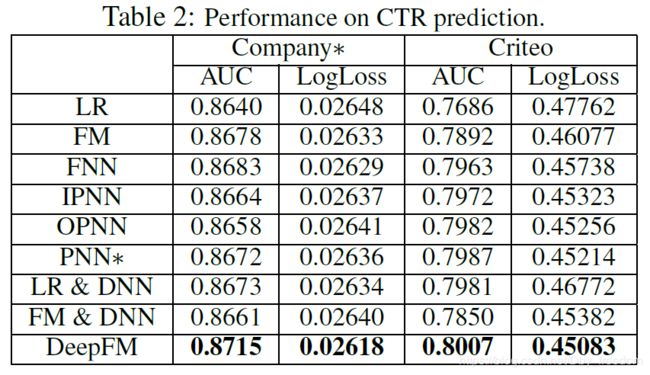
Effectiveness Comparison
时间结果如下表:
实验结论:
- 组合特征的学习提高了CTR预估模型的性能;
- 正确的同时学习低阶和高阶组合特征,同样可以提高CTR预估的性能;
- 在学习低阶和高阶组合特征时,使用相同的feature embedding可以提高CTR性能。
4.2 超参数建议
论文中还给出了一些参数的实验结果,直接给出结论,大家实现的时候可以参考下。
| 超参数 | 建议 | 备注 |
|---|---|---|
| 激活函数 | 1. IPNN使用tanh 2. 其余使用ReLU | |
| 学习方法 | Adam | |
| Dropout | 0.6~0.9 | |
| 隐藏层数量 | 3~5 | 根据实际数据大小调整 |
| 神经元数量 | 200~600 | 根据实际数据大小调整 |
| 网络形状 | constant | 一共有四种:固定、增长、下降、菱形。 |
PS: constant效果最好,就是隐藏层每一层的神经元的数量相同。
这部分实验图片太多,可直接参考原论文。
5. Note
对于一个基于CTR预估的推荐系统,最重要的是学习到用户点击行为背后隐含的特征组合。在不同的推荐场景中,低阶组合特征或者高阶组合特征可能都会对最终的CTR产生影响。
因子分解机(Factorization Machines, FM)通过对于每一维特征的隐变量内积来提取特征组合。最终的结果也非常好。但是,虽然理论上来讲FM可以对高阶特征组合进行建模,但实际上因为计算复杂度的原因一般都只用到了二阶特征组合。
那么对于高阶的特征组合来说,我们很自然的想法,通过多层的神经网络即DNN去解决。
下面的图片来自于张俊林教授在AI大会上所使用的PPT。
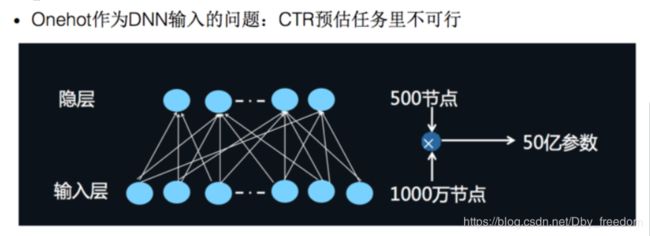
我们之前也介绍过了,对于离散特征的处理,我们使用的是将特征转换成为one-hot的形式,但是将One-hot类型的特征输入到DNN中,会导致网络参数太多:
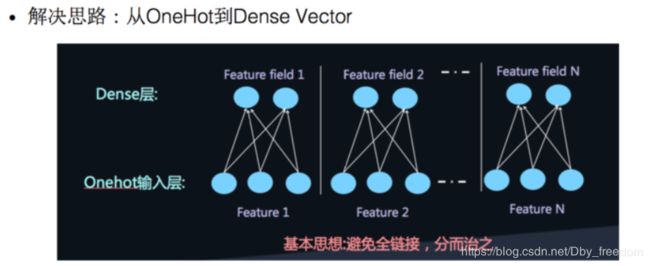
如何解决这个问题呢,类似于FFM中的思想,将特征分为不同的field:
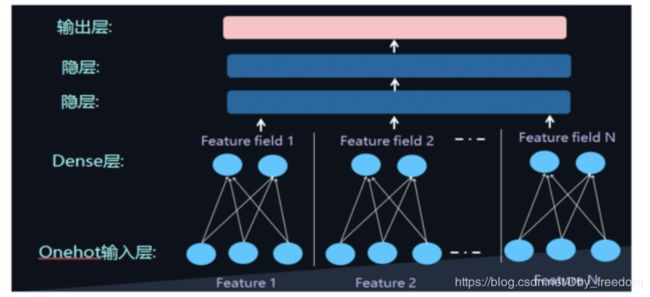
但是低阶和高阶特征组合隐含地体现在隐藏层中,如果我们希望把低阶特征组合单独建模,然后融合高阶特征组合。
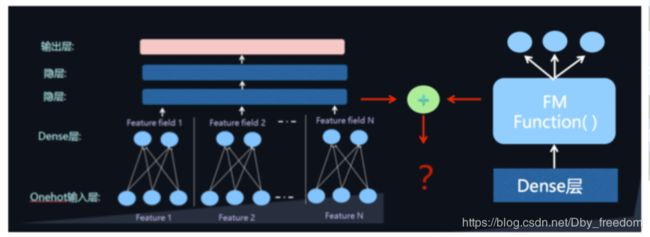
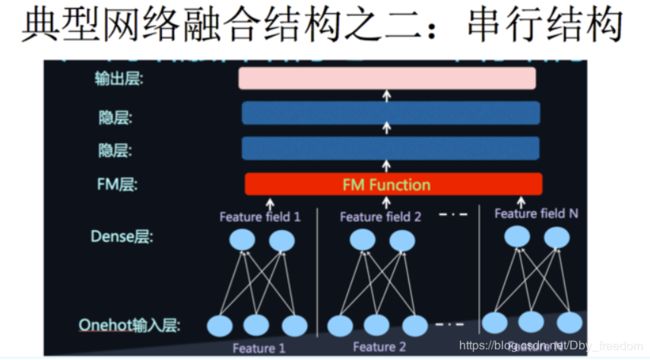
即将DNN与FM进行一个合理的融合:
二者的融合总的来说有两种形式,一是串行结构,二是并行结构。
串行结构代表是FNN,DeepFM就是并行结构中的一种典型代表。
参考文献
[1] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
[2] 推荐系统遇上深度学习(三)–DeepFM模型理论和实践
[3] 计算广告CTR预估系列(一)–DeepFM理论
[4] CTR预估专栏 | 一文搞懂DeepFM的理论与实践