【DFS入门例题】HDU1010,字典序
The maze was a rectangle with sizes N by M. There was a door in the maze. At the beginning, the door was closed and it would open at the T-th second for a short period of time (less than 1 second). Therefore the doggie had to arrive at the door on exactly the T-th second. In every second, he could move one block to one of the upper, lower, left and right neighboring blocks. Once he entered a block, the ground of this block would start to sink and disappear in the next second. He could not stay at one block for more than one second, nor could he move into a visited block. Can the poor doggie survive? Please help him.
'X': a block of wall, which the doggie cannot enter;
'S': the start point of the doggie;
'D': the Door; or
'.': an empty block.
The input is terminated with three 0's. This test case is not to be processed.
题目大意:有一只小狗被困在了一个N×M的矩形迷宫之中,小狗可以花费一秒的时间移动到与当前所在格子相邻(上下左右)的任一格子里,但每当小狗踏上一个格子,这个格子就会在一秒内下沉。因此小狗必须在格子之间不断移动且不能重复踏上同一个格子。迷宫中有一个格子是门,但门只会在第t秒钟开启,因此小狗必须要在第t秒时移到这一格子上才能逃出迷宫。
输入数据:第一行分别是三个整数(N M t),接下来是M行N列的字符,用来组成迷宫。S代表小狗开始时所在的格子,D表示门所在的格子,.表示小狗能移到这一格子上(当然,只能走一次),X表示这一格子是墙,不能通行。输入数据包含多组,若第一行的三个整数均为0,则代表程序结束。
输出数据:如果小狗能逃出迷宫则输出YES,反之则输出NO。
分析:从S和D之间不被X完全隔开,那么至少存在一条路径可以从S到达D,若这些路径中存在一条路径,其长度为t(如果S和D相邻,那么S到D的最短路径长度为1),则输出YES,反之输出NO。显然程序需要枚举出所有可能的路径直至找到一条符合要求的路径。
我们需要设置一根带有计时器的探针,令其初始坐标为S的坐标,计时器归零;每当探针移动到相邻坐标时,计时器数值加一并将这一格子标记;若格子为X或者已经被标记则探针不能移到这一格子上;当有以下三种情况时:1,探针无路可走、2,计时器超时(大于t)、3,探针移动到了D上但计时器数值不等于t,结束本轮探测转而进入下一轮探测,必须保证每一轮探测的路径不完全一致;当探针移动到了D且计时器为t时,结束所有探测并返回YES;如所有的路径均已被探测且未发现符合要求的路径,返回NO。
显然,这样的一根探针其实是在胡乱瞎走的(在某一轮探测中它完全可能走了一个蛇形的路线把自己给困了起来),因此虽然探针的作用是寻找D,但其实它做的是试图遍历整个迷宫。DFS正是我们需要采用的遍历方式。
DFS的全称为深度优先搜索,所谓的深度优先是指,在搜索过程中优先访问下一级节点(注意每个节点可能会有多个下一级节点),如无下一级节点可以访问则结束本轮搜索并返回上一级节点,开始新一轮搜索以访问之前未访问过的节点。如此重复直到数据结构中所有节点都被访问。
尽管DFS大多时候是用于遍历图状结构的,但为了方便起见先用一个树状结构进行讲解。
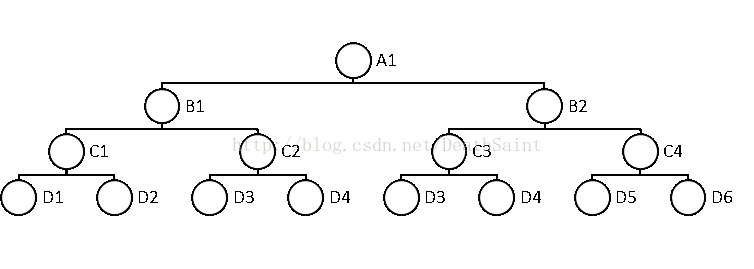
在如图所示的数据结构中,各个相邻的节点被线所连接,线是无方向的,这意味着既可以从A1访问B2也可以从B2访问A1,因而A1和B2互为对方的下一级节点,而上一级节点则由当前一轮搜索的路线所确立。如从A1开始搜索,当前路线为A1->B1->C1->D1,则C1为D1的上一级节点。
假设从A1开始DFS,优先访问下标最小的节点,显然第一轮搜索的路线为A1->B1->C1->D1,D1不存在下一级节点,故结束本轮搜索并返回上一级节点C1,开始新一轮搜索并访问之前未访问过的D2,注意每一轮搜索都是从A1开始的,第一轮搜索和第二轮搜索的路线在C1之前完全一致,故第二轮搜索的路线为A1->B1->C1->D2。不难看出,为了遍历这一数据结构共需进行6轮搜索,最后一轮搜索的路线为A1->B2->C4->D6,到此所有节点均被访问,DFS结束。
思考探针需要具备哪些部件才能完成遍历,显然任何搜索都需要有嗅探器,即在访问某一节点之前先嗅探该节点是否应该被访问,如不应该则返回,嗅探器同样可以用于嗅探数据结构的“边缘”,如上图中D层就是边缘(没有下一级节点)。
回到HDU1010上来,本题的数据结构其实是这样的形式。
(假设矩阵为3×3)
A1 -- A2 -- A3
| | |
B1 -- B2 -- B3
| | |
C1 -- C2 -- C3
对于该数据结构中非边缘的节点,都存在4个下一级节点,这样的矩形结构其实是非常简单的。现在开始设计探针。
嗅探器:嗅探已访问节点和边缘。
计时器:记录当前的时间,用来判断是否超时。
判断器:判断计时器超时和探针移动到了D上时计时器的情况,此外如果已经找到了一条符合要求的路线,那么之后的搜索都没必要了,这也可以加入到判断之中。
探针需要知道自己所处的节点位置,由于该结构是个矩形,所以可以采用平面坐标的方式来表示,同时每当探针访问了一个节点后都需要对它标记,因此我们需要一个布尔数组使数组里的每一个元素与每一个节点一一对应。
void dfs(int y, int x, int time){ //y代表纵坐标,x代表横坐标,time为计时器
//判断器
if(time > t || flag) //判断超时或者已经找到了符合要求的路线
return;
if(map[y][x]=='D'){ //判断探针到达D时计时器的情况,如果计时器恰为t则说明找
if(time == t){ //到了符合要求的路线,用变量flag来标记;如果计时器不为
flag = 1; //t,则结束本轮搜索并返回
return;
}
else return;
}
//嗅探器
if(map[y][x] != 'X'){ //嗅探是否是墙
judge[y][x] = 1; //不是墙,说明该节点可以访问,将它标记
if(x+1< a && !judge[y][x+1]) //嗅探右侧节点是否存在以及是否被访问
dfs(y, x+1, time+1);
if(x-1>=0 && !judge[y][x-1]) //嗅探左侧节点是否存在以及是否被访问
dfs(y, x-1, time+1);
if(y+1< b && !judge[y+1][x]) //嗅探上侧节点是否存在以及是否被访问
dfs(y+1, x, time+1);
if(y-1>=0 && !judge[y-1][x]) //嗅探下侧节点是否存在以及是否被访问
dfs(y-1, x, time+1);
judge[y][x] = 0; //下一级节点都被访问过了,需要结束搜索返回上一级,
//在这之前要把节点重新标记为未访问的状态
}
return;
}至此,本题的dfs讲解就完成了,但是题目还没有结束,如果直接就用这个探针去搜索路线的话,OJ系统会报超时!我们还需要一些优化策略。
设S的横纵坐标分别为start_x和start_y,D的横纵坐标分别为door_x和door_y。从S到D的理论最短路线为两条线段,即abs(start_x-door_x) + abs(start_y-door_y),若这一数值大于t,显然应该返回NO;而S到D的理论最长路线为一条遍历了迷宫每个格子的路线,其长度为N*M - 1,若这一数值小于t,显然也应该返回NO。
此外最重要的优化叫奇偶剪枝,即从S到D的任意路线的长度的奇偶型与理论最短路线是一致的。因为理论最短路线以外的其它所遇路线都可以理解成是对理论最短路线的绕路,比如在理论最短路线中,从节点A到B是走的直线,而别的路线则绕了一圈。在这个数据结构中探针只能走水平或竖直,因此无论绕出去多少步,都要走相同的步数回来,即因为绕路而增加的步数必然是偶数,故而奇偶型不变。因此如果t为偶数而理论最短路线长为奇数,也应该直接返回NO。
加上这三个优化之后的main函数部分与全局变量声明部分代码如下:
#include
#include
using namespace std;
bool judge[10][10], flag;
char map[10][10];
int a, b, t;
void dfs(int, int, int);
int main(){
while(1){
int i, j, start_y, start_x, door_x, door_y;
flag = 0;
memset(judge, 0, sizeof(judge));
cin>>b>>a>>t;
if(!(a + b + t)) break;
for(i=0; i < b; i++)
cin>>map[i];
for(i=0; i < b; i++)
for(j=0; j < a; j++){
if(map[i][j] == 'S'){
start_x = j;
start_y = i;
}
if(map[i][j] == 'D'){
door_x = i;
door_y = j;
}
}
if(abs(start_y - door_y) + abs(start_x - door_x) > t
|| (start_x + start_y + door_x + door_y + t) % 2 == 1){
cout<<"NO"< 【附】用DFS解决字典序全排列问题
题目描述
设计算法生成n个元素{r1,r2,…,rn}的全排列。n<=10
程序输入说明
程序输出说明
先解释一下字典序,最直观的理解就是:把每个字符都视作一个数字(0到9就是0到9,而a到z就视作是26进制的数字,且由a到z从小变大),这样n个字符就能组成一个n位的某一进制的数,比如abc就是一个26进制的三位数。显然可以组成的数不止一个,把可以组成的数字按从小到大排列,这个顺序就是字典序。
用DFS的思想来考虑,每一个排列其实就是一次搜索的路线,比如abc就是从字符a到字符b再到字符c的路线,由于每个字符都可能出现在任一位置上,所以这里的数据结构是图状结构,且为完全图(即任意两个节点间都存在连线),这样一来,对于任一字符,其下一级节点是其余所有字符。
让DFS优先搜索数值小的节点(a比b小;0比1小),这样搜索的顺序就是字典序。但是为了能优先搜索数值小的节点,需要对节点进行排序,也就是对输入的数据按ASCII码排序。但是调用dfs函数后,每轮搜索的路线的首个节点(也就是输出的第一个字符)是不变的,因此输入的字符有多少个就要在main函数里调用多少次dfs。
直接上代码了:
#include
#include
#include
char line[11], output[11];
bool flag[10];
void exchange(char *a, char *b){
char tmp;
tmp = *a; *a = *b; *b = tmp;
return;
}
void quicksort(int k, int j, char *a){
if(k >= j)
return;
int probe_1 = k,
probe_2 = j;
while(1){
while(a[probe_2] >= a[k] && probe_1 != probe_2)
probe_2--;
while(a[probe_1] <= a[k] && probe_1 != probe_2)
probe_1++;
if(probe_1 == probe_2)
break;
exchange(&a[probe_1], &a[probe_2]);
}
exchange(&a[k], &a[probe_1]);
quicksort(k, probe_1, a);
quicksort(probe_1+1, j, a);
return;
}
void dfs(int a, int count){
int i;
if(flag[a])
return;
flag[a] = 1;
output[count] = line[a]; //output数组按照搜索的路线依次存放字符
for(i=0; i < strlen(line); ++i)
dfs(i, count+1);
if(count == strlen(line) - 1){
output[strlen(line)] = '\0';
puts(output); //输出output
}
flag[a] = 0;
return;
}
int main(){
while(scanf("%s",line) != EOF){
int i;
quicksort(0,strlen(line)-1,line);
memset(flag, 0, sizeof(flag));
for(i=0; i < strlen(line); ++i)
dfs(i,0);
}
return 0;
} 上面代码的quicksort函数为快速排序函数,如果看不懂可以暂时不用理会,只要知道它是用来给字符串line按ASCII码从小到大排序的就行。
祝愿我们都能在ACM中取得佳绩!