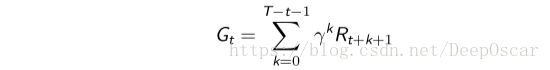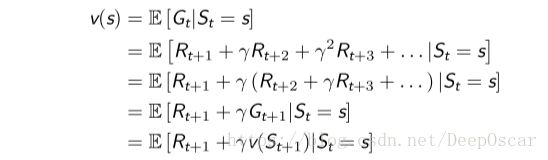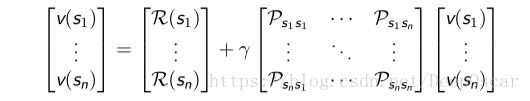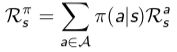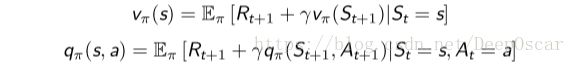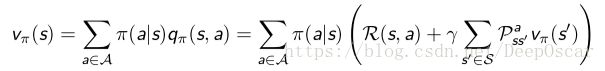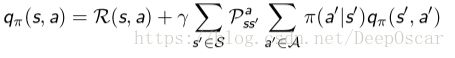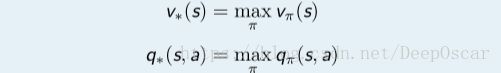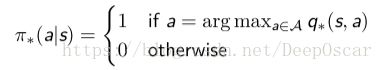第一课：一文读懂马尔科夫过程

1.马尔科夫决策过程（MDPs）简介

马尔科夫决策过程是对强化学习(RL)问题的数学描述。几乎所有的RL问题都能通过MDPs来描述：

• 最优控制问题可以用MDPs来描述;
• 部分观测环境可以转化成POMDPs;
• 赌博机问题是只有一个状态的MDPs;

注：虽然大部分DL问题都能转化为MDPs，但是以下所描述的MDPs是全观测的情况。

强化学习中的表述符号：

 

2.马尔科夫性

只要知道现在，将来和过去条件独立

定义：如果在t时刻的状态St满足如下等式，那么这个状态被称为马尔科夫状态，或者说该状态满足马尔科夫性。

• 马尔科夫性的要点：
• 状态St包含了所有历史相关信息
• 或者说历史的所有状态的相关信息都在当前状态St上体现出来
• 一旦St知道了，那么S1,S2, ... ,St-1都可以被抛弃
• 数学上可以认为：状态时将来的充分统计量
• 因此，这里要求环境时全观测

例子：

• 下棋时，只关心当前局面
• 打俄罗斯方块时，只关心当前屏幕

有了马尔科夫状态之后

• 定义状态转移矩阵
• 忽略时间的影响，只需要关心当前状态即做出下一步决策

注：这里的相关指问题相关，可能有一些问题无关的信息没有在St中；马尔科夫性和状态的定义息息相关。

 

3.状态转移矩阵

定义：状态转移概率是指从一个马尔科夫状态s跳转到后继状态s'的概率：

所有的状态组成行，所有的后继状态组成列，将得到状态转移矩阵：

其中，n表示状态的个数，由于P代表了整个状态转移的集合，所以用个花体。每行元素相加等于1。

我们也可以将状态转移概率写成函数的形式：

其中，状态数量太多或者是无穷大（连续状态）时，更适合用状态转移函数，此时，。

 

4.马尔科夫过程

一个马尔科夫过程（MP）是一个无记忆的随机过程，即一些马尔科夫状态的序列。

定义：马尔科夫过程可以由一个二元组定义。

S表示了状态集合，P描述了状态转移矩阵。

注，虽然我们有时候不知道P的具体值，但是通常我们假设P存在且稳定的。

当P不稳定时，不稳定环境，在线学习，快速学习。

举个栗子：

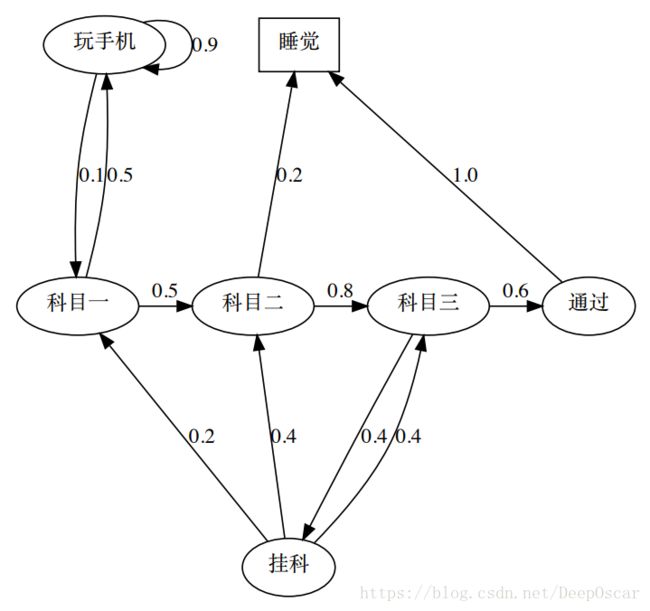
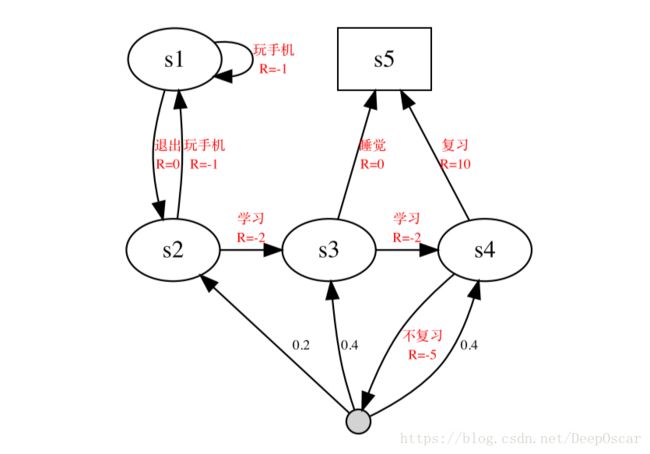
一个学生每天需要学习三个科目，然后通过测试。不过也有可能只学完两个科目之后直接睡觉，一旦挂科有可能需要重新学习某些科目。用椭圆表示普通状态，每一条线上的数字表示从一个状态跳转到另一个状态。方块表示终止状态。终止状态有两种：1是时间终止，2是状态终止。

 

由于马尔科夫郭晨够可以用图中的方块和线条组成，所以可以称马尔科夫过程为马尔科夫链（MDPs chain）。

 

6.片段

片段定义：强化学习中，从初始状态S1到终止状态的序列过程，被称为一个片段（episode），S1, S2，... ，ST

• 如果一个任务总以终止状态结束，那么这个任务被称为片段任务；
• 如果一个任务没有终止状态，会被无限执行下去，这被称为连续性任务。

还是来看上面的例子：

假设初始状态是“科目一”，从这个马尔科夫链中，我们可能采样到如下的片段：

 

1. “科目一”，“科目二”，“睡觉” 
2. “科目一”，“科目二”，“科目三”，“通过”，“睡觉”
3. “科目一”，“玩手机”，“玩手机”，…, “玩手机”，“科目一”, “科目二”, “睡觉”
4. “科目一”，“科目二”，“科目三”，“挂 科”，“科目二”，“科目三”，“挂科”，挂科“科目一”，“科目二”，“科 目三”，“挂科”, “科目三”，“通过”, “睡觉”

分别用 s1 ∼ s7 代表 “科目一”, “科目二”， “科目三”, “通过”, “挂科”, “玩手机”, “睡觉”

 

7.马尔科夫奖励过程（MRP）

马尔可夫过程主要描述的是状态之间的转移关系，在这个转移关系上 赋予不同的奖励值即得到了马尔可夫奖励过程。

定义：马尔可夫奖励 (Markov Reward Process, MRP) 过程由一个四元组组成 〈S, P,R, γ〉。

 

• S 代表了状态的集合
• P 描述了状态转移矩
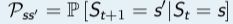
• R 表示奖励函数，R(s) 描述了在状态 s 的期望奖励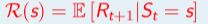，，某一个状态的
• γ 表示衰减因子，γ ∈ [0, 1]

注，以上要注意R和R的区别

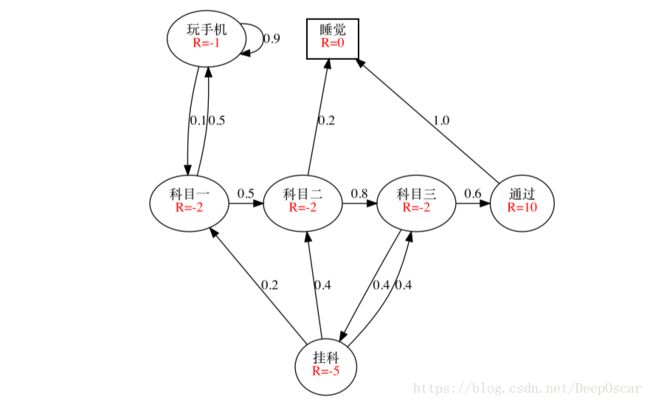
马尔可夫奖励过程的例子：

 

8.回报值

奖励值：对每一个状态的评价；

回报值：对每一个片段的评价。

定义：回报值（return Gt）是从时间t处开始的累计衰减奖励

对于片段性任务：

对于连续性任务：

 

片段的统一化表达：

终止状态等价于自身转移概率为1，奖励为0的状态

因此我们能够将片段任务和连续性任务统一表达：

这里T=∞时，表示连续性任务，否则即为片段性任务。

 

9.衰减值

为什么我们要使用遮掩给定指数衰减？

直观感觉

影响未来的因素不仅仅包含当前

我们对未来的把握也时逐渐衰减的

一般情况下，我们更关注短时间按的反馈

数学便利

 

• 一个参数就描述了整个衰减过程，只需要调节一个参数γ既可以调节长时间奖励的权衡（trade-off）
• 指数衰减形式又很容易进行数学分析
• 指数衰减是对回报值的有界保证，避免了循环 MRP 和连续性 MRP 情况下回报值变成无穷大

 

10.值函数

为什么要值函数？

 

• 回报值是一次片段的结果，存在很大的样本偏差
• 回报值的角标是t，值函数关注的是状态s

定义：一个MRP的值函数定义：

 

• 这里的值函数针对的是状态s，所以称为状态值函数，又称为V函数；
• Gt是一个随机变量
• 这里使用小写的v函数，代表了真实存在的值函数

通过一个例子比较值函数和回报值：

针对初始状态S1=“科目一”，且γ=0.5计算不同片段的回报值

虽然都是从相同的初始状态开始，但是不同的片段有不容的回报值，而且值函数是他们的期望值。

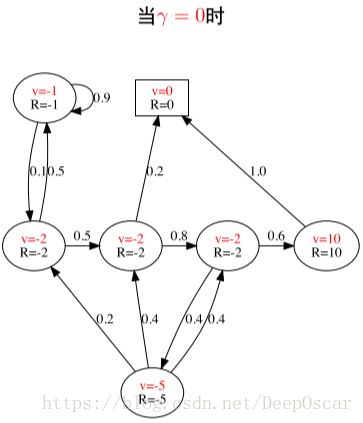
针对上述例子当γ取不同的值时对应的V值函数如下图：

    

 

11.MRPs 中的贝尔曼方程

值函数的表达式可以分解成两个部分

 

• 瞬时奖励 Rt+1
• 后继状态 St+1 的值函数乘上一个衰减系数

 

• 体现了v(s)与v(St+1)之间的迭代关系
• 这是强化学习中的核心理论之一
• 注意s小写，St+1大写

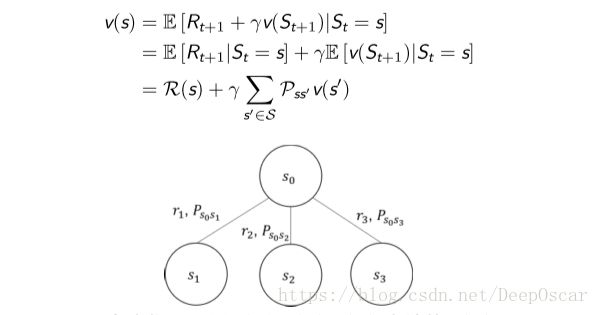
如果我们已知转移矩阵P，那么

图中我们可以用 v(s1), v(s2), v(s3) 去计算 v(s0)，由后继状态的值函数计算当前状态的值函数。

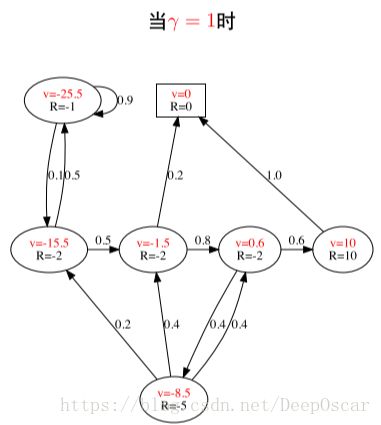
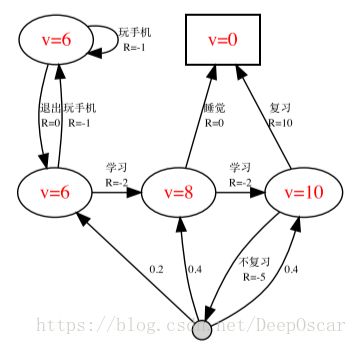
当γ=1时，我们根据以下例子计算值函数：

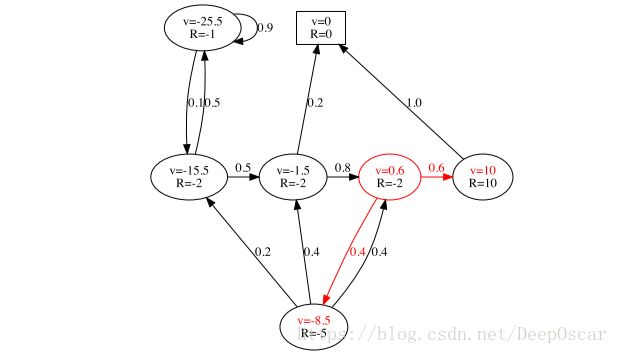
套用公式，红框状态的值函数v = -2+0.6*10+0.4*-8.5 = 0.6。

 

12.贝尔曼方程的矩阵形式

使用矩阵-向量的形式表达贝尔曼方程，即：

假设状态集合为 S = {s1, s2, . . . , sn}，那么

贝尔曼方程本质上是一个线性方程，可以直接求解：

 

• 计算复杂度O(n^3)
• 要求已知状态转移矩阵P
• 直接求解的方式仅限于小的MRPs

注：计算复杂度：

 

马尔科夫过程的最终目的是要产生决策，因此需要重点讨论马尔科夫决策过程

 

13.马尔科夫决策过程

马尔科夫决策过程(MDP)与MP、MRP的区别

 

• 在MP和MRP中，我们都是作为观察者，去观察其中的状态转移现象，去计算回报值
• 对于一个RL问题，我们更希望去改变状态转移的流程，去最大化回报值
• 通过MRP中引入决策即得到了马尔科夫决策过程

马尔科夫决策过程定义：一个马尔科夫决策过程由一个五元组构成 〈S, A, P,R, γ〉。

 

• S 代表了状态的集合；A 代表了动作的集合；P 描述了状态转移矩阵；
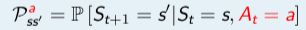• R 表示奖励函数，R(s, a) 描述了在状态 s做动作 a的奖励，；
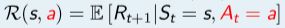• γ 表示衰减因子，γ ∈ [0, 1]

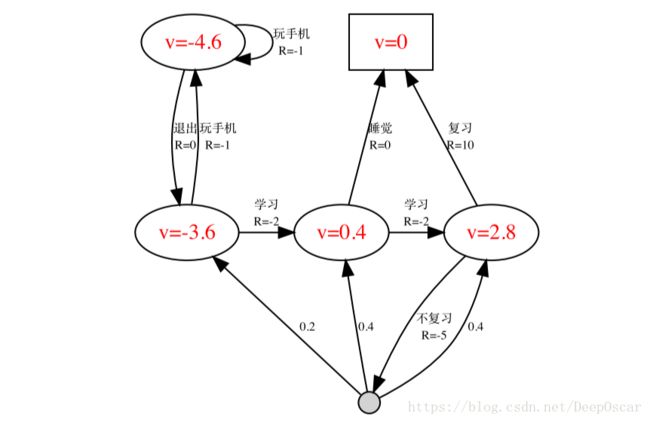
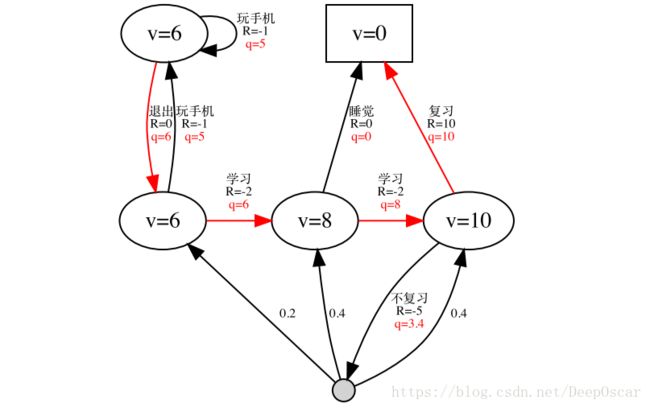
举个栗子说明马尔科夫决策过程：

针对状态的奖励变成了针对 〈s, a〉 的奖励；能通过动作进行控制的状态转移，由原来的状态转移概率变成了动作；MDP只关注那些可以做出决策的动作；被动的状态转移关系被压缩成一个状态，被动指无论做任何动作，状态都会发生跳转。这样的状态不属于MDP中考虑的状态，原图中，由于通过后一定去睡觉因此进行了压缩，原图中挂科后的跳转不受到控制。

注，图中除了在“科目三”的状态上执行“不复习”动作外，其他的所有状态跳转都是确定性，我们通过在不同的状态上执行不同的动作，即可实现状态跳转。

能够随意愿改变的就变成了动作。我们关心的是在什么情况先该做什么动作。

 

14.策略

我们将之前MRPs中的状态转移矩阵分成了两个部分

 

• 能被智能体控制的策略，policy；
• MDPs中的转移矩阵P(不受智能体控制，认为是环境的一部分)。

定义：在MDPs中，一个策略π是在给定状态下的动作的概率分布，。

假设动作是有限的，我们就会写成一个向量，向量上的值对应相应动作的概率，该向量求和为1，不同的状态就会对应不同的向量值。当为确定性策略的时候，就不是一个分布问题了，就是a=π。

 

• 策略是对智能体行为的全部描述，若策略给定，所有动作将被确定。
• 在MDPs中的策略是基于马尔科夫状态的（而不是基于历史的）
• 策略是时间稳定的，只和s有关，与时间t无关。
• 策略是RL问题的终极目标
• 如果策略的概率分布输出的是独热的，那么称为确定性策略，否则为随机策略。

 

15.MDP和MRP之间的关系

 

对于一个MDP问题 〈S, A, P,R, γ〉，如果给定了策略π，

MDP将会退化成MRP，

此时，，

策略π有两个含义，①当为确定性策略的时候，π就等于a表示一个动作；②当策略不确定的时候，就表示一个动作分布。

 

16.MDP中的值函数

在 MDPs 问题中，由于动作的引入，值函数分为了两种：①状态值函 数（V 函数）；②状态动作值函数 (Q 函数)。

①状态值函 数（V 函数）定义：MDPs 中的状态值函数是从状态s开始，使用策略π得到的期望回报值。

。

②状态动作值函数 (Q 函数)定义：MDPs 中的状态动作值函数是从状态 s 开始，执行动作 a，然后使用策略 π 得到的期望回报值。

注:MDPs 中，任何不说明策略π 的情况下，讨论值函数都是在耍流氓！

和 MRP 相似，MDPs 中的值函数也能分解成瞬时奖励和后继状态的值 函数两部分：

举个例子说明问题：

对于∀a, s 都有 π(a|s) = 0.5，且 γ = 1时，vπ(s)如下图所示：

将图中的圆圈状态从上到下从左到右分别记为 s1, s2, s3, s4，将终止状态记 为 s5，则当 π(a|s) = 0.5∀a, s 时，状态转移矩阵为：

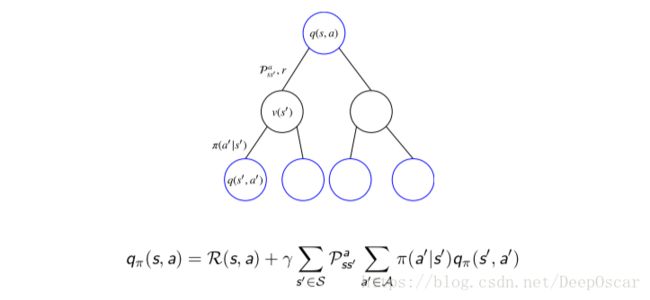
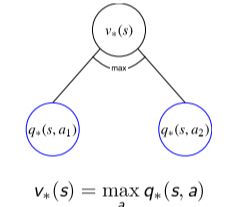
V 函数与 Q 函数之间的相互转化：

  

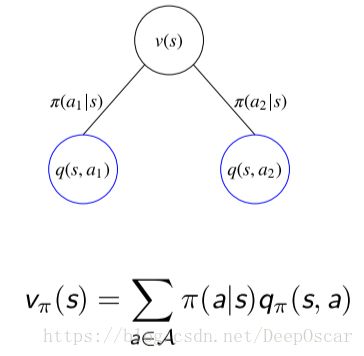
V-Q : 

在状态s的情况下，有两个可行的动作，我们采用π分别取执行每一个动作的概率分别为π(a1 | s)和π(a2 | s)。

①执行a1动作的情况下，得到的动作状态值q(s, a 1)；

①执行a2动作的情况下，得到的动作状态值q(s, a 2)；

上图表示，上边圆圈的值可以通过下边圆圈的值求得。

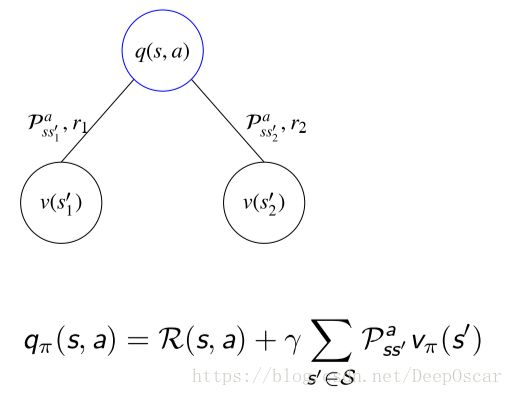
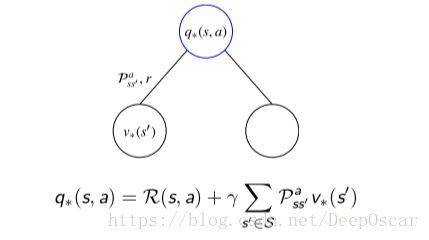
Q-V' :

而q是和下一状态的v是有关系的， q表示当前状态下做了一个动作a，做动作a后就会发生两个跳转，假设跳转也有两种可能分别为s1'和s2'，中间会获得奖励r1和r2。花体的R代表了期望的意思。

 

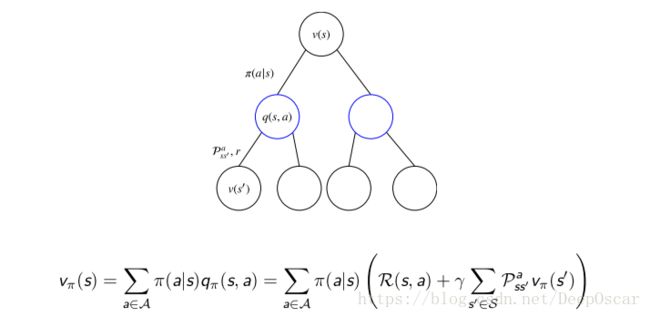
17.贝尔曼期望方程V 函数和Q 函数

贝尔曼期望方程V 函数:

表达了MDP中的vπ(s)和vπ(s′)之间的关系。

实际上等价于， 为什么？

 

思考：

.... ...

 

贝尔曼期望方程Q函数：

 

实际上等价于， 为什么？

思考：

.... ...

 

18.贝尔曼期望方程例子

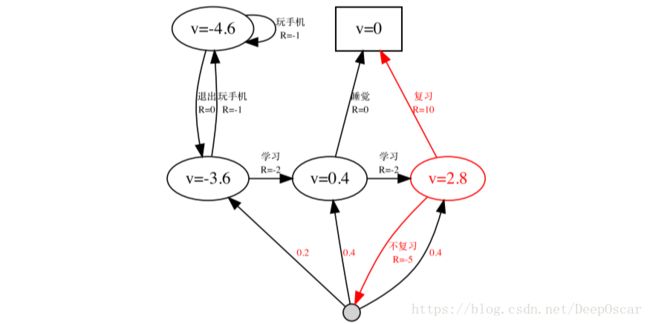
当γ=1，π(a|s) = 0.5时，

套用以上公式可以计算图中红圈之内的vπ(s)= 0.5 × (10 + 0) + 0.5 × (−5 + 0.2 ×−3.6 + 0.4 × 0.4 + 0.4 × 2.8)=2.8 

 

19.贝尔曼期望方程的矩阵形式

MDPs 下的贝尔曼期望方程和 MRP 的形式相同，

同样地，可以直接求解

求解的要求：①已知 π(a|s)；②已知

 

20.最优值函数

之前值函数，以及贝尔曼期望方程针对的都是给定策略 π 的情况，是 一个评价的问题。
现在我们来考虑强化学习中的优化问题，即找出最好的策略。

定义：最优值函数指的是在所有策略中的值函数最大值，其中包括最优 V 函 数和最优 Q 函数：

最优值函数指的是一个 MDP 中所能达到的最佳性能；

如果我们找到最优值函数即相当于这个 MDP 已经解决了。

最优 V 函数和最优 Q 函数：

当 γ = 1 时的最优 V 函数 v∗(s)；                             当 γ = 1 时的最优 Q 函数 q∗(s, a)；

    

 

21.最有策略

为了比较不同策略的好坏，我们首先定义策略的比较关系：

定理：

对于任何MDP问题，

 

• 总存在一个策略π*要好于或等于其他所有的策略，π∗ ≥ π, ∀π；
• 所有的最优策略都能够实现最优的 V 函数 vπ∗(s) = v∗(s)
• 所有的最优策略都能够实现最优的 Q 函数 qπ∗(s,a) = q∗(s,a)

怎么得到最优策略?

当我们已知了最优 Q 函数后，我们能够马上求出最优策略，只要根据 q∗(s, a) 选择相应的动作即可。

 

• 可以看出对于任何 MDPs 问题，总存在一个确定性的最优策略

如果已知最优 V 函数，能不能找到最优策略呢？

答：

思考

... ...

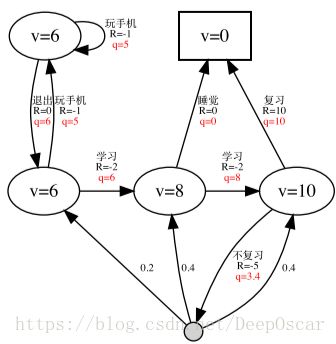
再次举个例子说明问题：

当 γ = 1 时的最优策略 π∗(a|s)

 

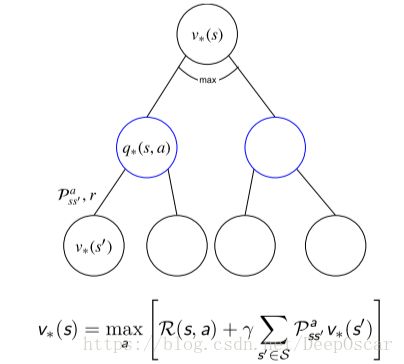
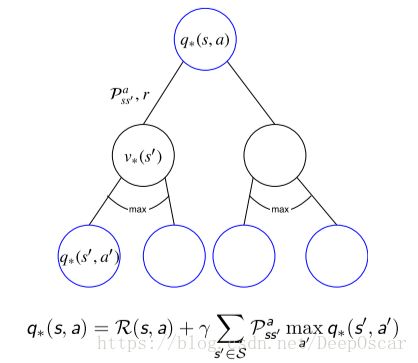
22.v∗ 与 q∗ 的相互转化

之前我们已经探讨了 vπ(s) 和 qπ(s, a) 之间的关系——贝尔曼期望方程，同样地，v∗(s) 和 q∗(s, a) 也存在递归的关系——贝尔曼最优方程。

  

和贝尔曼期望方程的关系：

 

贝尔曼最优方程——V 函数；                                              贝尔曼最优方程——Q 函数

  

 

最优值函数和和贝尔曼期望方程的关系:

 

• 贝尔曼最优方程本质上就是利用了 π∗ 的特点，将求期望的算子转 化成了 MAXa
• 在贝尔曼期望方程中，π 是已知的。而在贝尔曼最优方程中，π∗ 是未知的
• 解贝尔曼期望方程的过程即对应了评价，解贝尔曼最优方程的过程即对应了优化

解贝尔曼最优方程:

 

 

• 贝尔曼最优方程不是线性的 
• 一般很难有闭式的解
• 可以使用迭代优化的方法去解 ：值迭代、策略迭代 、Q 学习、SARSA ...

23.MDPs 的拓展

 

无穷或连续 MDPs 

 

 

• 动作空间或状态空间无限可数 
• 动作空间或状态空间无限不可数 (连续)
• 时间连续

部分可观测 MDPs（Partially observable MDPs, POMDPs）

 

 

• 此时观测不等于状态 Ot ≠ St 
• POMDPs 由七元组构成 < S, A, O, P,R, Z, γ >
• Z 是观测函数：
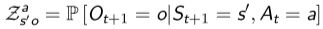
• 观测不满足马尔可夫性，因此也不满足贝尔曼方程 
• 状态未知，隐马尔可夫过程
• 有时对于 POMDPs 来说，最优的策略是随机性的

无衰减 MDPs

 

 

• 用于各态历经马尔可夫决策过程 ，各态历经性：平稳随机过程的一种特性 
• 存在独立于状态的平均奖赏
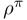
• 求值函数时，需要减去该平均奖赏，否则有可能奖赏爆炸

（结束，累炸了...）