PSO解决TSP问题（粒子群算法解决旅行商问题）--python实现

首先感谢这位github上的Marcos Castro de Souza大神

本文利用代码链接如下：https://github.com/marcoscastro/tsp_pso，此代码使用python实现，我用于此实例的代码稍作修改。

欢迎私戳关注这位大神！

有问题欢迎私戳我->给我写信

首先来看一下什么是TSP：

wiki解释

 

The travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in operations research and theoretical computer science.

通俗来讲就是，给定n个城市，n个城市之间两两连通，求一条能从一个城市A出发，访问完所有n个城市，并最终回到该城市A的路线，使得该路线所耗费的成本最小，在本例中即路程最小（也可以自定义两两城市之间的耗费权重，实现更复杂的分析）。

下面对该问题举个实例，进行实现。

 

• 假设有9个城市，以0~8标记；
• 城市间均两两通行；
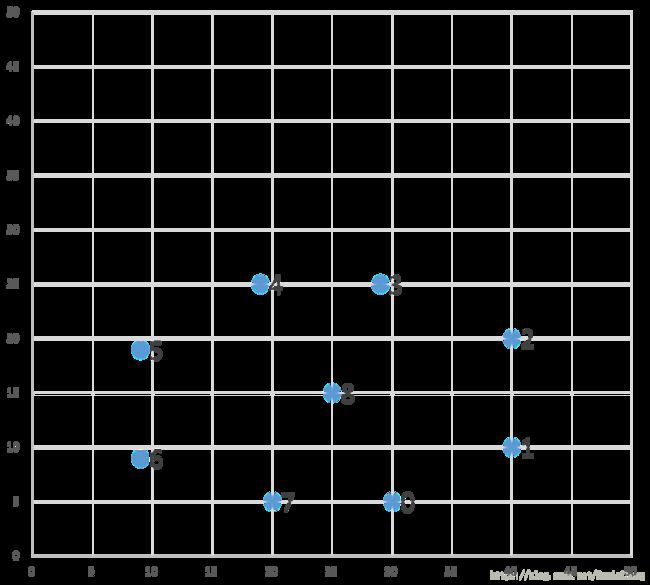
• 城市位置分别是(30, 5), (40, 10), (40, 20), (29, 25), (19, 25), (9, 19), (9, 9), (20, 5),(25,15)；

路径表达为城市序号的组合，如012345678等。

解决算法的核心是路径序号的交换，将序号的顺序作为该粒子的速度。

可以看到城市分布是这样子的。

然后直接上代码吧，

首先导入所用的python包

from operator import attrgetter
import random, sys, time, copy

其次定义Graphic类和路径生成类，在graphic类中可以方便的对城市及各城市之间权重进行表示

# class that represents a graph
class Graph:

	def __init__(self, amount_vertices):
		self.edges = {} # dictionary of edges
		self.vertices = set() # set of vertices
		self.amount_vertices = amount_vertices # amount of vertices


	# adds a edge linking "src" in "dest" with a "cost"
	def addEdge(self, src, dest, cost = 0):
		# checks if the edge already exists
		if not self.existsEdge(src, dest):
			self.edges[(src, dest)] = cost
			self.vertices.add(src)
			self.vertices.add(dest)


	# checks if exists a edge linking "src" in "dest"
	def existsEdge(self, src, dest):
		return (True if (src, dest) in self.edges else False)


	# shows all the links of the graph
	def showGraph(self):
		print('Showing the graph:\n')
		for edge in self.edges:
			print('%d linked in %d with cost %d' % (edge[0], edge[1], self.edges[edge]))

	# returns total cost of the path
	def getCostPath(self, path):
		
		total_cost = 0
		for i in range(self.amount_vertices - 1):
			total_cost += self.edges[(path[i], path[i+1])]

		# add cost of the last edge
		total_cost += self.edges[(path[self.amount_vertices - 1], path[0])]
		return total_cost


	# gets random unique paths - returns a list of lists of paths
	def getRandomPaths(self, max_size):

		random_paths, list_vertices = [], list(self.vertices)

		initial_vertice = random.choice(list_vertices)
		if initial_vertice not in list_vertices:
			print('Error: initial vertice %d not exists!' % initial_vertice)
			sys.exit(1)

		list_vertices.remove(initial_vertice)
		list_vertices.insert(0, initial_vertice)

		for i in range(max_size):
			list_temp = list_vertices[1:]
			random.shuffle(list_temp)
			list_temp.insert(0, initial_vertice)

			if list_temp not in random_paths:
				random_paths.append(list_temp)

		return random_paths

# class that represents a complete graph
class CompleteGraph(Graph):

	# generates a complete graph
	def generates(self):
		for i in range(self.amount_vertices):
			for j in range(self.amount_vertices):
				if i != j:
					weight = random.randint(1, 10)
					self.addEdge(i, j, weight)

然后定义粒子类

# class that represents a particle
class Particle:

	def __init__(self, solution, cost):

		# current solution
		self.solution = solution

		# best solution (fitness) it has achieved so far
		self.pbest = solution

		# set costs
		self.cost_current_solution = cost
		self.cost_pbest_solution = cost

		# velocity of a particle is a sequence of 4-tuple
		# (1, 2, 1, 'beta') means SO(1,2), prabability 1 and compares with "beta"
		self.velocity = []

	# set pbest
	def setPBest(self, new_pbest):
		self.pbest = new_pbest

	# returns the pbest
	def getPBest(self):
		return self.pbest

	# set the new velocity (sequence of swap operators)
	def setVelocity(self, new_velocity):
		self.velocity = new_velocity

	# returns the velocity (sequence of swap operators)
	def getVelocity(self):
		return self.velocity

	# set solution
	def setCurrentSolution(self, solution):
		self.solution = solution

	# gets solution
	def getCurrentSolution(self):
		return self.solution

	# set cost pbest solution
	def setCostPBest(self, cost):
		self.cost_pbest_solution = cost

	# gets cost pbest solution
	def getCostPBest(self):
		return self.cost_pbest_solution

	# set cost current solution
	def setCostCurrentSolution(self, cost):
		self.cost_current_solution = cost

	# gets cost current solution
	def getCostCurrentSolution(self):
		return self.cost_current_solution

	# removes all elements of the list velocity
	def clearVelocity(self):
		del self.velocity[:]

最后定义一个PSO算法类

# PSO algorithm
class PSO:

	def __init__(self, graph, iterations, size_population, beta=1, alfa=1):
		self.graph = graph # the graph
		self.iterations = iterations # max of iterations
		self.size_population = size_population # size population
		self.particles = [] # list of particles
		self.beta = beta # the probability that all swap operators in swap sequence (gbest - x(t-1))
		self.alfa = alfa # the probability that all swap operators in swap sequence (pbest - x(t-1))

		# initialized with a group of random particles (solutions)
		solutions = self.graph.getRandomPaths(self.size_population)

		# checks if exists any solution
		if not solutions:
			print('Initial population empty! Try run the algorithm again...')
			sys.exit(1)

		# creates the particles and initialization of swap sequences in all the particles
		for solution in solutions:
			# creates a new particle
			particle = Particle(solution=solution, cost=graph.getCostPath(solution))
			# add the particle
			self.particles.append(particle)

		# updates "size_population"
		self.size_population = len(self.particles)


	# set gbest (best particle of the population)
	def setGBest(self, new_gbest):
		self.gbest = new_gbest

	# returns gbest (best particle of the population)
	def getGBest(self):
		return self.gbest


	# shows the info of the particles
	def showsParticles(self):

		print('Showing particles...\n')
		for particle in self.particles:
			print('pbest: %s\t|\tcost pbest: %d\t|\tcurrent solution: %s\t|\tcost current solution: %d' \
				% (str(particle.getPBest()), particle.getCostPBest(), str(particle.getCurrentSolution()),
							particle.getCostCurrentSolution()))
		print('')


	def run(self):

		# for each time step (iteration)
		for t in range(self.iterations):

			# updates gbest (best particle of the population)
			self.gbest = min(self.particles, key=attrgetter('cost_pbest_solution'))

			# for each particle in the swarm
			for particle in self.particles:

				particle.clearVelocity() # cleans the speed of the particle
				temp_velocity = []
				solution_gbest = copy.copy(self.gbest.getPBest()) # gets solution of the gbest
				solution_pbest = particle.getPBest()[:] # copy of the pbest solution
				solution_particle = particle.getCurrentSolution()[:] # gets copy of the current solution of the particle

				# generates all swap operators to calculate (pbest - x(t-1))
				for i in range(self.graph.amount_vertices):
					if solution_particle[i] != solution_pbest[i]:
						# generates swap operator
						swap_operator = (i, solution_pbest.index(solution_particle[i]), self.alfa)

						# append swap operator in the list of velocity
						temp_velocity.append(swap_operator)

						# makes the swap
						aux = solution_pbest[swap_operator[0]]
						solution_pbest[swap_operator[0]] = solution_pbest[swap_operator[1]]
						solution_pbest[swap_operator[1]] = aux

				# generates all swap operators to calculate (gbest - x(t-1))
				for i in range(self.graph.amount_vertices):
					if solution_particle[i] != solution_gbest[i]:
						# generates swap operator
						swap_operator = (i, solution_gbest.index(solution_particle[i]), self.beta)

						# append swap operator in the list of velocity
						temp_velocity.append(swap_operator)

						# makes the swap
						aux = solution_gbest[swap_operator[0]]
						solution_gbest[swap_operator[0]] = solution_gbest[swap_operator[1]]
						solution_gbest[swap_operator[1]] = aux

				
				# updates velocity
				particle.setVelocity(temp_velocity)

				# generates new solution for particle
				for swap_operator in temp_velocity:
					if random.random() <= swap_operator[2]:
						# makes the swap
						aux = solution_particle[swap_operator[0]]
						solution_particle[swap_operator[0]] = solution_particle[swap_operator[1]]
						solution_particle[swap_operator[1]] = aux
				
				# updates the current solution
				particle.setCurrentSolution(solution_particle)
				# gets cost of the current solution
				cost_current_solution = self.graph.getCostPath(solution_particle)
				# updates the cost of the current solution
				particle.setCostCurrentSolution(cost_current_solution)

				# checks if current solution is pbest solution
				if cost_current_solution < particle.getCostPBest():
					particle.setPBest(solution_particle)
					particle.setCostPBest(cost_current_solution)

接下来就是解决实际问题的部分啦。

首先输入城市的列表，循环加入各城市间路线的权重。

if __name__ == "__main__":

   #输入城市坐标数组
	cities = [(30,5),(40,10),(40,20),(29,25),(19,25),(9,19),(9,9),(20,5),(25,15)]
	
	# 初始化图
	graph = Graph(amount_vertices=len(cities))
	
	#计算距离作为边的权重
	for i in range(0,len(cities)):
		for j in range(0,len(cities)):
			if i != j:
				distance = pow((cities[i][0]-cities[j][0])**2+(cities[i][1]-cities[j][1])**2,0.5)
				graph.addEdge(i, j, distance)
			
	#生成PSO，此处分别设置迭代次数，粒子群数量，β值，α值	
	pso = PSO(graph, iterations=1000, size_population=5000, beta=1, alfa=0.9)
	# 执行PSO
	pso.run() 
	#展示粒子
	pso.showsParticles() 

	# 展示全局最佳粒子
	print('gbest: %s | cost: %d\n' % (pso.getGBest().getPBest(), pso.getGBest().getCostPBest()))	

 

结果如下：

 

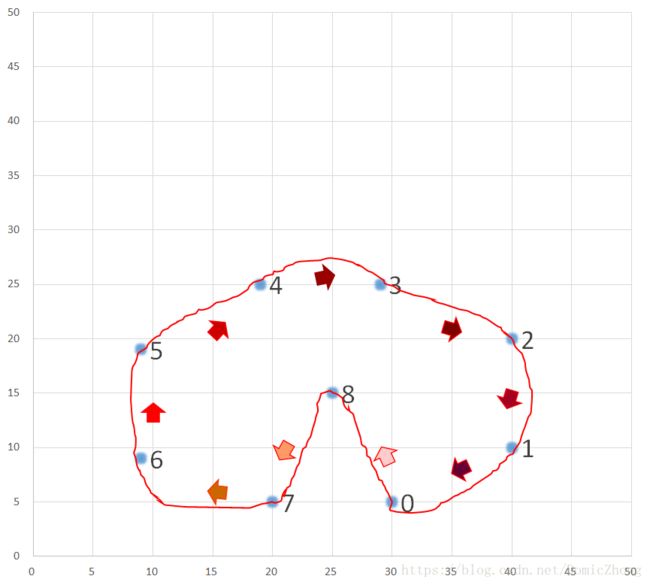
可以看到最佳路径为 0, 8, 7, 6, 5, 4, 3, 2, 1 所需的路程耗费为: 98

路线如下，箭头由浅到深进行遍历，解决各TSP问题都是爱你的形状！！！

 

完美解决问题！！！

更多GIS算法分享，请持续关注DomicZhong的博客！