数据结构--树--线索二叉树(中序,前序,后序)
线索二叉树
在遍历二叉树的时候,会有许多空指针域,这些空间不存储任何事物,白白浪费了内存的资源。那么在做遍历的时候,提前记录下每个结点的前驱和后继,这样就更加节约了时间。
[ lchild ] [ LTag ] [ data ] [ RTag ] [ rchild ]
LTag = { 0 : lchild 域指示结点的左孩子 1 : lchild 域指示结点的前驱 }
RTag = { 0 : rchild 域指示结点的右孩子 1 : rchild 域指示结点的后继 }
以这种结点结构构成的二叉链表作为二叉树的存储结构,叫做 线索链表,其中,指向结点前驱和后继的指针,叫做 线索。
加上线索的二叉树叫做 线索二叉树(Threaded Binary Tree)
对二叉树以某种次序遍历使其变成线索二叉树的过程叫做 线索化
★线索二叉树结构:
#define TElemType char
typedef enum{
Link,Thread
}PointerTag;//Link == 0 :指针 ,Thread == 1: 线索
typedef struct BiThrNode{
TElemType data;
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag , RTag; //左右标志
}BiThrNode, *BiThrTree;[ lchild ] [ LTag ] [ data ] [ RTag ] [ rchild ]
LTag = { 0 : lchild 域指示结点的左孩子 1 : lchild 域指示结点的前驱 }
RTag = { 0 : rchild 域指示结点的右孩子 1 : rchild 域指示结点的后继 }
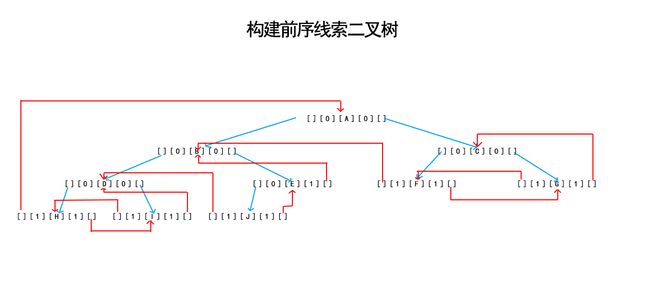
★线索化二叉树之前,咱们先把树建起来(用前序遍历建树)
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};
int i=0;
//二叉树的创建
Status CreatBiThrTree(BiThrTree &T)
{
if(Vexch[i++]=='$') T=NULL;
else
{
T= (BiThrTree)malloc(sizeof(BiThrNode));
if(!T) return 0;
T->data=Vexch[i-1];//生成根节点
printf("%5c",T->data);
T->LTag=Link;
CreatBiThrTree(T->lchild);//创建左子树
T->RTag=Link;
CreatBiThrTree(T->rchild);//创建右子树
}
return 1;
} 建立树为该树:
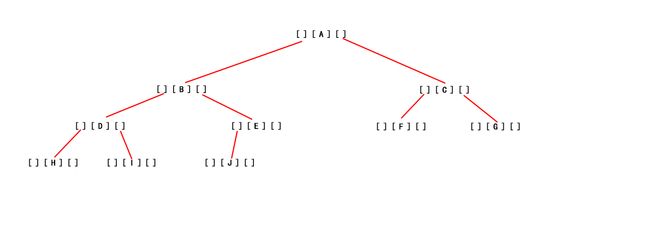
遍历visit()函数
Status visit(TElemType e){
printf("%5c",e);
return OK;
}
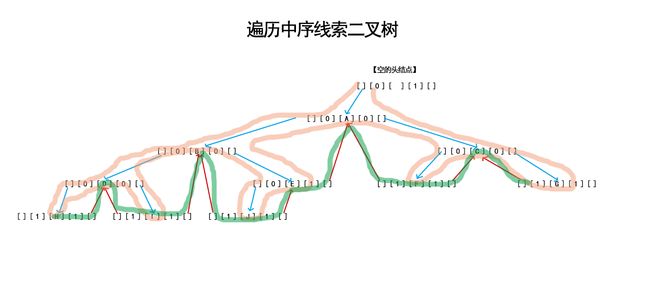
(1)中序遍历,线索二叉树
【 让一棵树 直接变成一个线性表去遍历】遍历 顺序为:H - >D - > I - > B - > J - > E - > A - > F - > C - > G
【建立二叉树头结点】(下面的代码没有循环,只是单纯的建立了一个头结点,连接上主体的树部分,方便遍历。)
//建立头结点,中序线索二叉树
Status InOrderThreading(BiThrTree &Thrt,BiThrTree T){
//中序遍历二叉树T,并将其中序线索化,Thrt指向头结点。
if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode))))
return ERROR;
Thrt->RTag = Link; //建头结点
Thrt->rchild = Thrt ; //右指针回指
if(!T){
Thrt->lchild = Thrt;
Thrt->LTag = Link;
}else{
pre = Thrt ;
Thrt->lchild = T;
Thrt->LTag = Link;
InThreading(T);
pre->rchild = Thrt ;
pre->RTag = Thread;
Thrt->rchild = pre;
}
return OK;
}Thrt 就是 下图的空指针, 初始化 pre 为 这个空指针,完成下图的 【1】【2】步骤
做完树的线索化后,pre 已经到了最后一个节点,那么就可以完成 【3】【4】两个步骤了
如下图所示。
【1】让最左的结点,就是中序遍历时 第一个结点的左指针指向 空的头结点。
【第一个结点的左标记肯定是 Thread而不是 link ,这样就能找到最左的结点】 那么既然是线索Thread,就让他指向空的头结点(反正空着也是空着)
【2】头结点顺下来,从左子树开始找
【3】因为空节点的右标记是 Thread线索,那么让他指向最右的,最终结点。(反正空着也是空着)
【4】最终结点G的右线索指向头结点,标记着终结。
构成循环:
↓ → → → → 【 空的头结点】 ← ← ← ← ↑
H → D → I → B → J → E → A → F → C → G

★LTag = { 0 : lchild 域指示结点的左孩子 1 : lchild 域指示结点的前驱 } RTag = { 0 : rchild 域指示结点的右孩子 1 : rchild 域指示结点的后继 }
概括为:LTag=0(Link)【左孩子】,LTag=1(Thread)【前驱】;RTag=0(Link)【右孩子】 ,RTag=1(Thread)【后继】
【问】那么怎样的称为Link指针 ,怎样的 称为 Thread 线索
【答】可以这样理解,Link指针是本来建树的时候就有的,而Thread线索是为了线索化,而增添的。
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点。
void InThreading(BiThrTree p){
if(p){
InThreading(p->lchild); //左子树线索化
if(!p->lchild){ //没有左孩子
p->LTag = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(!pre->rchild){
pre->RTag = Thread; //后继线索
pre->rchild = p ; //前驱右孩子指针指向后继
}
pre = p;
InThreading(p->rchild); //右子树线索化
}
}首先,很明显:中序遍历线索化,其实也是基于中序遍历的。(从代码中可以看出)
也是先左,再中,后右(左 > 中 > 右)
只是在中间部分,对结点的处理的时候,有些不一样。1、中序遍历时是输出。2、而现在我们把它替换为 处理标记和指针。
介绍如何处理,很简单:
★没有左孩子,或者没有右孩子那肯定是线索,而不是指针
★因为是中序,遍历肯定是从左到右,那么左边的线索肯定是指向前驱的,右边的线索肯定是指向后继的。
【中序遍历】
//中序 遍历线索二叉树
Status InOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
//T指向头结点,头结点的左链lchild指向根节点,可参见线索化算法
//中序遍历二叉线索树T的非递归算法,对每个数据元素调用函数visit
BiThrTree p ;
p = T->lchild; // p指向根节点
while(p != T){ //空树 或者遍历结束时 p == T
while(p->LTag == Link ) // 走到最左结点
p = p->lchild;
visit(p->data);
while(p->RTag == Thread && p->rchild !=T){
p = p->rchild ; // 若有右线索,
visit(p->data);
}
p = p->rchild;
}
return OK;
}最外面的while 从上面构造的时候就已经说明了,当p回到T的时候,那么就标记结束了。
里面的第一个 while(p->LTag == Link) 循环,走到最左结点
输出该节点
while(p->RTag == Thread && p->rchild !=T) 如果右边有线索,且指向的不是最后的根T, 优先按着线索走。
发现这里没有线索了,那么就继续往右孩子找。
【总的中序遍历线索二叉树代码】
#include
#include
#include
#include
using namespace std;
#define Status int
#define OK 1
#define ERROR 0
#define TElemType char
typedef enum{
Link,Thread
}PointerTag;//Link == 0 :指针 ,Thread == 1: 线索
typedef struct BiThrNode{
TElemType data;
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag , RTag; //左右标志
}BiThrNode, *BiThrTree;
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};
int i=0;
//二叉树的创建
Status CreatBiThrTree(BiThrTree &T)
{
if(Vexch[i++]=='$') T=NULL;
else
{
T= (BiThrTree)malloc(sizeof(BiThrNode));
if(!T) return 0;
T->data=Vexch[i-1];//生成根节点
printf("%5c",T->data);
T->LTag=Link;
CreatBiThrTree(T->lchild);//创建左子树
T->RTag=Link;
CreatBiThrTree(T->rchild);//创建右子树
}
return 1;
}
Status visit(TElemType e){
printf("%5c",e);
return OK;
}
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点。
void InThreading(BiThrTree p){
if(p){
InThreading(p->lchild); //左子树线索化
if(!p->lchild){ //没有左孩子
p->LTag = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(!pre->rchild){
pre->RTag = Thread; //后继线索
pre->rchild = p ; //前驱右孩子指针指向后继
}
pre = p;
InThreading(p->rchild); //右子树线索化
}
}
//建立头结点,中序线索二叉树
Status InOrderThreading(BiThrTree &Thrt,BiThrTree T){
//中序遍历二叉树T,并将其中序线索化,Thrt指向头结点。
if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode))))
return ERROR;
Thrt->RTag = Link; //建头结点
Thrt->rchild = Thrt ; //右指针回指
if(!T){
Thrt->lchild = Thrt;
Thrt->LTag = Link;
}else{
pre = Thrt ;
Thrt->lchild = T;
Thrt->LTag = Link;
InThreading(T);
pre->rchild = Thrt ;
pre->RTag = Thread;
Thrt->rchild = pre;
}
return OK;
}
//中序 遍历线索二叉树
Status InOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
//T指向头结点,头结点的左链lchild指向根节点,可参见线索化算法
//中序遍历二叉线索树T的非递归算法,对每个数据元素调用函数visit
BiThrTree p ;
p = T->lchild; // p指向根节点
while(p != T){ //空树 或者遍历结束时 p == T
while(p->LTag == Link ) // 走到最左结点
p = p->lchild;
visit(p->data);
while(p->RTag == Thread && p->rchild !=T){
p = p->rchild ; // 若有右线索,
visit(p->data);
}
p = p->rchild;
}
return OK;
}
int main()
{
BiThrTree T, inorderT;
printf("创建树\n");
CreatBiThrTree(T);
printf("\n中序遍历线索二叉树\n");
InOrderThreading(inorderT , T);
InOrderTraverse_Thr(inorderT , visit);
printf("\n");
return 0;
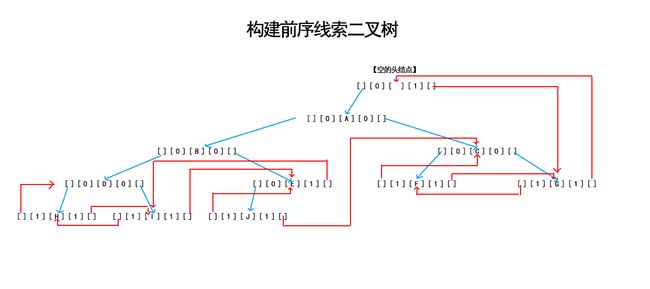
} (2)前序遍历,线索二叉树
【前序遍历二叉树线索化】
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点。
void PreThreading(BiThrTree p){
if(p){
if(!p->lchild){ //没有左孩子
p->LTag = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(!pre->rchild && pre){
pre->RTag = Thread; //后继线索
pre->rchild = p ; //前驱右孩子指针指向后继
}
pre = p;
if(p->LTag == Link)
PreThreading(p->lchild); //左子树线索化
if(p->RTag == Link)
PreThreading(p->rchild); //右子树线索化
}
}//建立头结点,前序线索二叉树
Status PreOrderThreading(BiThrTree &Thrt,BiThrTree T){
//前序遍历二叉树T,并将其前序线索化,Thrt指向头结点。
if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode))))
return ERROR;
Thrt->RTag = Thread; //建头结点
Thrt->rchild = Thrt ; //右指针回指
Thrt->LTag = Link;
if(!T){
Thrt->lchild = Thrt;
}else{
Thrt->lchild = T;
pre = Thrt ;
PreThreading(T);
pre->rchild = Thrt ;
pre->RTag = Thread;
Thrt->rchild = pre;
}
return OK;
} ↓ ← 【 空的头结点 】 ← ← ← ← ← ← ← ↑
A → B → D → H → I → E → J → C → F → G
1、A的直接前驱
㈠若LTag 的值为1,那么LChild 所指结点就是直接前驱
㈡若LTag 的值为0,那么
⒈若A为双亲左儿子,那么直接前驱就是A的双亲结点
⒉若A为双亲右儿子,那么直接前驱就是A的双亲左儿子
2、A的直接后继
㈠若RTag 的值为1,那么RChild 所指结点就是直接后继
㈡若RTag 的值为0,那么
⒈若LTag 的值为0,那么直接后继就是其左儿子。
⒉若LTag 的值为1,那么直接后继就是其右儿子。
【前序遍历二叉树】
//前序 遍历线索二叉树
Status PreOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
//T指向头结点,头结点的左链lchild指向根节点,可参见线索化算法
//前序遍历二叉线索树T的非递归算法,对每个数据元素调用函数visit
BiThrTree p ;
p = T->lchild; // p指向根节点
while(p != T){ //空树 或者遍历结束时 p == T
visit(p->data);
if(p->LTag == Link)
p = p->lchild;
else
p = p->rchild;
}
return OK;
}【总的前序遍历线索二叉树代码】
#include
#include
#include
#include
using namespace std;
#define Status int
#define OK 1
#define ERROR 0
#define TElemType char
typedef enum{
Link,Thread
}PointerTag;//Link == 0 :指针 ,Thread == 1: 线索
typedef struct BiThrNode{
TElemType data;
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag , RTag; //左右标志
}BiThrNode, *BiThrTree;
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};
int i=0;
//二叉树的创建
Status CreatBiThrTree(BiThrTree &T)
{
if(Vexch[i++]=='$') T=NULL;
else
{
T= (BiThrTree)malloc(sizeof(BiThrNode));
if(!T) return 0;
T->data=Vexch[i-1];//生成根节点
printf("%5c",T->data);
T->LTag=Link;
CreatBiThrTree(T->lchild);//创建左子树
T->RTag=Link;
CreatBiThrTree(T->rchild);//创建右子树
}
return 1;
}
Status visit(TElemType e){
printf("%5c",e);
return OK;
}
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点。
void PreThreading(BiThrTree p){
if(p){
if(!p->lchild){ //没有左孩子
p->LTag = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(!pre->rchild){
pre->RTag = Thread; //后继线索
pre->rchild = p ; //前驱右孩子指针指向后继
}
pre = p;
if(p->LTag == Link)
PreThreading(p->lchild); //左子树线索化
if(p->RTag == Link)
PreThreading(p->rchild); //右子树线索化
}
}
//建立头结点,前序线索二叉树
Status PreOrderThreading(BiThrTree &Thrt,BiThrTree T){
//前序遍历二叉树T,并将其前序线索化,Thrt指向头结点。
if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode))))
return ERROR;
Thrt->RTag = Thread; //建头结点
Thrt->rchild = Thrt ; //右指针回指
Thrt->LTag = Link;
if(!T){
Thrt->lchild = Thrt;
}else{
Thrt->lchild = T;
pre = Thrt ;
PreThreading(T);
pre->rchild = Thrt ;
pre->RTag = Thread;
Thrt->rchild = pre;
}
return OK;
}
//前序 遍历线索二叉树
Status PreOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
//T指向头结点,头结点的左链lchild指向根节点,可参见线索化算法
//前序遍历二叉线索树T的非递归算法,对每个数据元素调用函数visit
BiThrTree p ;
p = T->lchild; // p指向根节点
while(p != T){ //空树 或者遍历结束时 p == T
visit(p->data);
if(p->LTag == Link)
p = p->lchild;
else
p = p->rchild;
}
return OK;
}
int main()
{
BiThrTree T, PreT;
printf("创建树\n");
CreatBiThrTree(T);
printf("\n前序遍历线索二叉树\n");
PreOrderThreading(PreT , T);
PreOrderTraverse_Thr(PreT , visit);
printf("\n");
return 0;
} (3)后序遍历,线索二叉树
【后序遍历线索二叉树时,需要一个parent 指针,所以建树的时候与上面两个有所不同】
#define TElemType char
typedef enum{
Link,Thread
}PointerTag;//Link == 0 :指针 ,Thread == 1: 线索
typedef struct BiThrNode{
TElemType data;
struct BiThrNode *lchild, *rchild; //左右孩子指针
struct BiThrNode *parent;
PointerTag LTag , RTag; //左右标志
}BiThrNode, *BiThrTree;
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点。
Status visit(TElemType e){
printf("%5c",e);
return OK;
}
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};
int i=0;
//二叉树的创建
Status CreatBiThrTree(BiThrTree &T,BiThrTree &p)
{
if(Vexch[i++]=='$') T=NULL;
else
{
T= (BiThrTree)malloc(sizeof(BiThrNode));
if(!T) return 0;
T->data=Vexch[i-1];//生成根节点
T->parent = p;//指回原来的结点
visit(T->data);
T->LTag=Link;
CreatBiThrTree(T->lchild,T);//创建左子树
T->RTag=Link;
CreatBiThrTree(T->rchild,T);//创建右子树
}
return 1;
} void PostThreading(BiThrTree p){
if(p){
PostThreading(p->lchild); //左子树线索化
PostThreading(p->rchild); //右子树线索化
if(!p->lchild){ //没有左孩子
p->LTag = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(pre && !pre->rchild){
pre->RTag = Thread; //后继线索
pre->rchild = p ; //前驱右孩子指针指向后继
}
pre = p;
}
}【建立头结点】(这里就不建头结点了,因为入口是总根节点,出口也是总根节点)
1、A的直接前驱
㈠若LTag 的值为1,那么A的直接前驱为LChild所指结点
㈡若LTag 的值为0,那么
⒈若有左儿子,那么直接前驱就是A的左儿子。
⒉若有右儿子,那么直接前驱就是A的右儿子。
2、A的直接后继
㈠若结点A是二叉树的根,则其后继为空
㈡若结点A是其双亲的右儿子,或是双亲的左孩子且其双亲没有左子树没有右子树,则其后继即为双亲结点
㈢若结点A是其双亲的左儿子,且双亲有右子树,则其后继为双亲的右子树上按后序遍历列出来的第一个结点。
【后序遍历二叉树】
//后序 遍历线索二叉树
Status PostOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
BiThrTree p ;
p = T; // p指向根节点
pre=NULL;
while(p != NULL){ //空树 或者遍历结束时 p == T
while(p->LTag == Link ) // 走到最左结点 ||左结点
p = p->lchild;
while(p->RTag == Thread ){ //访问后继 ||右结点
visit(p->data);
pre = p;
p = p->rchild ;
}
if(p == T){ //是否是最后根节点
visit(p->data);
break;
}
while(p && p->rchild == pre ){ //访问根 ||根节点
visit(p->data);
pre = p;
p = p->parent;
}
if(p && p->RTag == Link)
p = p->rchild;
}
return OK;
}
【总的后序遍历线索二叉树代码】
#include
#include
#include
#include
using namespace std;
#define Status int
#define OK 1
#define ERROR 0
#define TElemType char
typedef enum{
Link,Thread
}PointerTag;//Link == 0 :指针 ,Thread == 1: 线索
typedef struct BiThrNode{
TElemType data;
struct BiThrNode *lchild, *rchild; //左右孩子指针
struct BiThrNode *parent;
PointerTag LTag , RTag; //左右标志
}BiThrNode, *BiThrTree;
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点。
Status visit(TElemType e){
printf("%5c",e);
return OK;
}
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};
int i=0;
//二叉树的创建
Status CreatBiThrTree(BiThrTree &T,BiThrTree &p)
{
if(Vexch[i++]=='$') T=NULL;
else
{
T= (BiThrTree)malloc(sizeof(BiThrNode));
if(!T) return 0;
T->data=Vexch[i-1];//生成根节点
T->parent = p;
visit(T->data);
T->LTag=Link;
CreatBiThrTree(T->lchild,T);//创建左子树
T->RTag=Link;
CreatBiThrTree(T->rchild,T);//创建右子树
}
return 1;
}
void PostThreading(BiThrTree p){
if(p){
PostThreading(p->lchild); //左子树线索化
PostThreading(p->rchild); //右子树线索化
if(!p->lchild){ //没有左孩子
p->LTag = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(pre && !pre->rchild){
pre->RTag = Thread; //后继线索
pre->rchild = p ; //前驱右孩子指针指向后继
}
pre = p;
}
}
//后序 遍历线索二叉树
Status PostOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
BiThrTree p ;
p = T; // p指向根节点
pre=NULL;
while(p != NULL){ //空树 或者遍历结束时 p == T
while(p->LTag == Link ) // 走到最左结点 ||左结点
p = p->lchild;
while(p->RTag == Thread ){ //访问后继 ||右结点
visit(p->data);
pre = p;
p = p->rchild ;
}
if(p == T){ //是否是最后根节点
visit(p->data);
break;
}
while(p && p->rchild == pre ){ //访问根 ||根节点
visit(p->data);
pre = p;
p = p->parent;
}
if(p && p->RTag == Link)
p = p->rchild;
}
return OK;
}
int main()
{
BiThrTree PostT;
printf("创建树\n");
pre = NULL;
CreatBiThrTree(PostT,pre);
printf("\n后序遍历线索二叉树\n");
PostThreading(PostT);
PostOrderTraverse_Thr(PostT , visit);
printf("\n");
return 0;
} 【问】为什么用先序遍历建树后,可以用来中序遍历线索化?
【答】先序遍历建树,只是一种建树方式(当然可以用别的方法来建树,但是数组里的顺序可能就要变化了),建完树后,跟后面线索化无关。
【问】为什么中序遍历,先序遍历,后序遍历在线索化的时候,要用不同的线索化?
【答】因为中序,先序,后序,他们的前驱和后继是不一样的,根据代码也知道是不一样。
【问】对于做题,画已知二叉树的前序、中序、后序线索二叉树有什么技巧吗?
【答】可以先将 二叉树前序、中序、后序遍历 顺序写出来。再根据写出来的顺序对二叉树进行线索化。
【问】接上,线索化的时候这么乱,不知道线索改连到哪里?
【答】每个结点左右各有一个指针,除了用于建树的“蓝色”线之外,我们只看红色的线索这条线。每个结点只要是线索的部分,左边就是指向排在该结点之前的那个结点,右边就是指排在该节点之后的那个结点,这也就是为什么要先把遍历的顺序提前写好的原因。