Udacity Deep Learning课程作业（六）

来到课程最后一次小作业，训练完word2vec模型后，作业六基于Text8.zip语料训练一个LSTM模型，用perplexity评价训练得到语言模型的质量，越低越好。

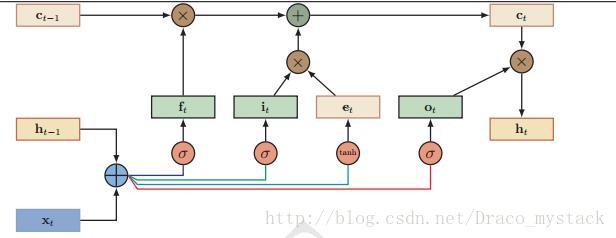
LSTM

Problem 1

num_nodes = 64

graph = tf.Graph()
with graph.as_default():

    # Parameters:
    # Input gate: input, previous output, and bias. 
    ix = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1)) # 27*64
    im = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    ib = tf.Variable(tf.zeros([1, num_nodes])) # 1*64
    # Forget gate: input, previous output, and bias.
    fx = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1)) # 27*64
    fm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    fb = tf.Variable(tf.zeros([1, num_nodes])) # 1*64
    # Memory cell: input, state and bias.                             
    cx = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1)) # 27*64
    cm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    cb = tf.Variable(tf.zeros([1, num_nodes])) # 1*64
    # Output gate: input, previous output, and bias.
    ox = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1)) # 27*64
    om = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    ob = tf.Variable(tf.zeros([1, num_nodes])) # 1*64

    # 改动，拼接同类的tensor
    tmp_x = tf.concat([ix, fx, cx, ox], 1) # 27*(64+64+64+64) = 27*256
    tmp_m = tf.concat([im, fm, cm, om], 1) # 64*(64+64+64+64) = 64*256
    tmp_b = tf.concat([ib, fb, cb, ob], 1) # 1*(64+64+64+64) = 1*256

    # Variables saving state across unrollings.
    saved_output = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
    saved_state = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
    # Classifier weights and biases.
    w = tf.Variable(tf.truncated_normal([num_nodes, vocabulary_size], -0.1, 0.1))
    b = tf.Variable(tf.zeros([vocabulary_size]))

#   # Definition of the cell computation.
#     def lstm_cell(i, o, state):
#         """Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
#         Note that in this formulation, we omit the various connections between the
#         previous state and the gates."""
#         input_gate = tf.sigmoid(tf.matmul(i, ix) + tf.matmul(o, im) + ib)
#         forget_gate = tf.sigmoid(tf.matmul(i, fx) + tf.matmul(o, fm) + fb)
#         update = tf.matmul(i, cx) + tf.matmul(o, cm) + cb
#         state = forget_gate * state + input_gate * tf.tanh(update)
#         output_gate = tf.sigmoid(tf.matmul(i, ox) + tf.matmul(o, om) + ob)
#         return output_gate * tf.tanh(state), state

    def lstm_cell(i, o, state):
        """Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
        Note that in this formulation, we omit the various connections between the
        previous state and the gates."""
        print(i.shape, '*', tmp_x.shape, '+', o.shape, '*', tmp_m.shape, '+', tmp_b.shape)
        smatmul = tf.matmul(i, tmp_x) + tf.matmul(o, tmp_m) + tmp_b 
        smatmul_input, smatmul_forget, update, smatmul_output = tf.split(smatmul, 4, 1)
        input_gate = tf.sigmoid(smatmul_input)
        forget_gate = tf.sigmoid(smatmul_forget)
        output_gate = tf.sigmoid(smatmul_output)
        state = forget_gate * state + input_gate * tf.tanh(update)
        return output_gate * tf.tanh(state), state

    # Input data.
    train_data = list()
    for _ in range(num_unrollings + 1):
        train_data.append(
          tf.placeholder(tf.float32, shape=[batch_size,vocabulary_size]))
    train_inputs = train_data[:num_unrollings]
    train_labels = train_data[1:]  # labels are inputs shifted by one time step.


    # Unrolled LSTM loop.
    outputs = list()
    output = saved_output
    state = saved_state
    for i in train_inputs:
        output, state = lstm_cell(i, output, state)
        outputs.append(output)

    # State saving across unrollings.
    with tf.control_dependencies([saved_output.assign(output),
                                saved_state.assign(state)]):
        # Classifier.
        logits = tf.nn.xw_plus_b(tf.concat(outputs, 0), w, b)
        loss = tf.reduce_mean(
          tf.nn.softmax_cross_entropy_with_logits(
            labels=tf.concat(train_labels, 0), logits=logits))

    # Optimizer.
    global_step = tf.Variable(0)
    learning_rate = tf.train.exponential_decay(
        10.0, global_step, 5000, 0.1, staircase=True)
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    gradients, v = zip(*optimizer.compute_gradients(loss))
    gradients, _ = tf.clip_by_global_norm(gradients, 1.25)
    optimizer = optimizer.apply_gradients(
        zip(gradients, v), global_step=global_step)

    # Predictions.
    train_prediction = tf.nn.softmax(logits)

    # Sampling and validation eval: batch 1, no unrolling.
    sample_input = tf.placeholder(tf.float32, shape=[1, vocabulary_size])
    saved_sample_output = tf.Variable(tf.zeros([1, num_nodes]))
    saved_sample_state = tf.Variable(tf.zeros([1, num_nodes]))
    reset_sample_state = tf.group(
        saved_sample_output.assign(tf.zeros([1, num_nodes])),
        saved_sample_state.assign(tf.zeros([1, num_nodes])))
    sample_output, sample_state = lstm_cell(
        sample_input, saved_sample_output, saved_sample_state)
    with tf.control_dependencies([saved_sample_output.assign(sample_output),
                            saved_sample_state.assign(sample_state)]):
        sample_prediction = tf.nn.softmax(tf.nn.xw_plus_b(sample_output, w, b))

输出结果：

(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 27) * (27, 256) + (64, 64) * (64, 256) + (1, 256)
(1, 27) * (27, 256) + (1, 64) * (64, 256) + (1, 256) 

运行计算：

num_steps = 7001
summary_frequency = 100

with tf.Session(graph=graph) as session:
  tf.global_variables_initializer().run()
  print('Initialized')
  mean_loss = 0
  for step in range(num_steps):
    batches = train_batches.next()
    feed_dict = dict()
    for i in range(num_unrollings + 1):
      feed_dict[train_data[i]] = batches[i]
    _, l, predictions, lr = session.run(
      [optimizer, loss, train_prediction, learning_rate], feed_dict=feed_dict)
    mean_loss += l
    if step % summary_frequency == 0:
      if step > 0:
        mean_loss = mean_loss / summary_frequency
      # The mean loss is an estimate of the loss over the last few batches.
      print(
        'Average loss at step %d: %f learning rate: %f' % (step, mean_loss, lr))
      mean_loss = 0
      labels = np.concatenate(list(batches)[1:])
      print('Minibatch perplexity: %.2f' % float(
        np.exp(logprob(predictions, labels))))
      if step % (summary_frequency * 10) == 0:
        # Generate some samples.
        print('=' * 80)
        for _ in range(5):
          feed = sample(random_distribution())
          sentence = characters(feed)[0]
          reset_sample_state.run()
          for _ in range(79):
            prediction = sample_prediction.eval({sample_input: feed})
            feed = sample(prediction)
            sentence += characters(feed)[0]
          print(sentence)
        print('=' * 80)
      # Measure validation set perplexity.
      reset_sample_state.run()
      valid_logprob = 0
      for _ in range(valid_size):
        b = valid_batches.next()
        predictions = sample_prediction.eval({sample_input: b[0]})
        valid_logprob = valid_logprob + logprob(predictions, b[1])
      print('Validation set perplexity: %.2f' % float(np.exp(
        valid_logprob / valid_size)))

Problem 2

引入embedding层，用embedding代替输入

# 1. introduce embedding lookup on input

num_nodes = 64
embedding_size = 100 # embedding层的维度

graph = tf.Graph()
with graph.as_default():

    # Parameters:
    vocabulary_embeddings = tf.Variable(
        tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0)) # 增加vocabulary_embeddings
    # Input gate: input, previous output, and bias. 
    ix = tf.Variable(tf.truncated_normal([embedding_size, num_nodes], -0.1, 0.1)) # 修改输入为100*64
    im = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    ib = tf.Variable(tf.zeros([1, num_nodes])) # 1*64
    # Forget gate: input, previous output, and bias.
    fx = tf.Variable(tf.truncated_normal([embedding_size, num_nodes], -0.1, 0.1)) # 修改输入为100*64
    fm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    fb = tf.Variable(tf.zeros([1, num_nodes])) # 1*64
    # Memory cell: input, state and bias.                             
    cx = tf.Variable(tf.truncated_normal([embedding_size, num_nodes], -0.1, 0.1)) # 修改输入为100*64
    cm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    cb = tf.Variable(tf.zeros([1, num_nodes])) # 1*64
    # Output gate: input, previous output, and bias.
    ox = tf.Variable(tf.truncated_normal([embedding_size, num_nodes], -0.1, 0.1)) # 修改输入为100*64
    om = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1)) # 64*64
    ob = tf.Variable(tf.zeros([1, num_nodes])) # 1*64

    # 改动，拼接同类的tensor
    tmp_x = tf.concat([ix, fx, cx, ox], 1) # 100*(64+64+64+64) = 100*256
    tmp_m = tf.concat([im, fm, cm, om], 1) # 64*(64+64+64+64) = 64*256
    tmp_b = tf.concat([ib, fb, cb, ob], 1) # 1*(64+64+64+64) = 1*256

    # Variables saving state across unrollings.
    saved_output = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
    saved_state = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
    # Classifier weights and biases.
    w = tf.Variable(tf.truncated_normal([num_nodes, vocabulary_size], -0.1, 0.1))
    b = tf.Variable(tf.zeros([vocabulary_size]))

#   # Definition of the cell computation.
#     def lstm_cell(i, o, state):
#         """Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
#         Note that in this formulation, we omit the various connections between the
#         previous state and the gates."""
#         input_gate = tf.sigmoid(tf.matmul(i, ix) + tf.matmul(o, im) + ib)
#         forget_gate = tf.sigmoid(tf.matmul(i, fx) + tf.matmul(o, fm) + fb)
#         update = tf.matmul(i, cx) + tf.matmul(o, cm) + cb
#         state = forget_gate * state + input_gate * tf.tanh(update)
#         output_gate = tf.sigmoid(tf.matmul(i, ox) + tf.matmul(o, om) + ob)
#         return output_gate * tf.tanh(state), state

    def lstm_cell(i, o, state):
        """Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
        Note that in this formulation, we omit the various connections between the
        previous state and the gates."""
        print(i.shape, '*', tmp_x.shape, '+', o.shape, '*', tmp_m.shape, '+', tmp_b.shape)
        smatmul = tf.matmul(i, tmp_x) + tf.matmul(o, tmp_m) + tmp_b 
        smatmul_input, smatmul_forget, update, smatmul_output = tf.split(smatmul, 4, 1)
        input_gate = tf.sigmoid(smatmul_input)
        forget_gate = tf.sigmoid(smatmul_forget)
        output_gate = tf.sigmoid(smatmul_output)
        state = forget_gate * state + input_gate * tf.tanh(update)
        return output_gate * tf.tanh(state), state

    # Input data.
    train_data = list()
    for _ in range(num_unrollings + 1):
        train_data.append(
          tf.placeholder(tf.float32, shape=[batch_size, vocabulary_size]))
    train_inputs = train_data[:num_unrollings]
    train_labels = train_data[1:]  # labels are inputs shifted by one time step.


    # Unrolled LSTM loop.
    outputs = list()
    output = saved_output
    state = saved_state
    for i in train_inputs:
#         output, state = lstm_cell(i, output, state)
#         outputs.append(output)
        i_embed = tf.nn.embedding_lookup(vocabulary_embeddings, tf.argmax(i, dimension=1)) # 增加embedding代替input
        output, state = lstm_cell(i_embed, output, state) # 对embedding计算lstm
        outputs.append(output)

    # State saving across unrollings.
    with tf.control_dependencies([saved_output.assign(output),
                                saved_state.assign(state)]):
        # Classifier.
        logits = tf.nn.xw_plus_b(tf.concat(outputs, 0), w, b)
        loss = tf.reduce_mean(
          tf.nn.softmax_cross_entropy_with_logits(
            labels=tf.concat(train_labels, 0), logits=logits))

    # Optimizer.
    global_step = tf.Variable(0)
    learning_rate = tf.train.exponential_decay(
        10.0, global_step, 5000, 0.1, staircase=True)
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    gradients, v = zip(*optimizer.compute_gradients(loss))
    gradients, _ = tf.clip_by_global_norm(gradients, 1.25)
    optimizer = optimizer.apply_gradients(
        zip(gradients, v), global_step=global_step)

    # Predictions.
    train_prediction = tf.nn.softmax(logits)

    # Sampling and validation eval: batch 1, no unrolling.
    sample_input = tf.placeholder(tf.float32, shape=[1, vocabulary_size])
    sample_input_embedding = tf.nn.embedding_lookup(vocabulary_embeddings, \
        tf.argmax(sample_input, dimension=1)) # 增加sample的embedding层
    saved_sample_output = tf.Variable(tf.zeros([1, num_nodes]))
    saved_sample_state = tf.Variable(tf.zeros([1, num_nodes]))
    reset_sample_state = tf.group(
        saved_sample_output.assign(tf.zeros([1, num_nodes])),
        saved_sample_state.assign(tf.zeros([1, num_nodes])))
    sample_output, sample_state = lstm_cell(
        sample_input_embedding, saved_sample_output, saved_sample_state) # 调用sample_input_embedding
    with tf.control_dependencies([saved_sample_output.assign(sample_output),
                            saved_sample_state.assign(sample_state)]):
        sample_prediction = tf.nn.softmax(tf.nn.xw_plus_b(sample_output, w, b))

输出结果：

(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(64, 100) * (100, 256) + (64, 64) * (64, 256) + (1, 256)
(1, 100) * (100, 256) + (1, 64) * (64, 256) + (1, 256) 

运行计算得到：

Initialized
Average loss at step 0: 3.308872 learning rate: 10.000000
Minibatch perplexity: 27.35
================================================================================
zs sb  ote t qdw  zprfe jphd vejodhr g e gqa y tkog geit s y tedxdp s acsbay ey 
e stfvwjjotsaqngu ihbnzelhprqsy  sdr r aaix ar de fon o eotc nefc wj fbiwwfksh n
nalev evtiz hr ymxkp  pxelccez ada s   p aazm bhmv te kobpie hcj  ile crcnwceqo 
royrtn  ou gihvsthtre rhysv cbzliebtse oone acbrloqonx dc b ezyikn db aea x hpqc
cth cuh i jojhfkcrtt cuh  fwo un todnar eo  c e ennj gqlgki  suwytptm ii sr e   
================================================================================
Validation set perplexity: 19.24
Average loss at step 100: 2.301575 learning rate: 10.000000
Minibatch perplexity: 10.12
Validation set perplexity: 8.71
Average loss at step 200: 2.016815 learning rate: 10.000000
Minibatch perplexity: 6.75
Validation set perplexity: 7.50
Average loss at step 300: 1.909146 learning rate: 10.000000
Minibatch perplexity: 6.09
Validation set perplexity: 6.59
Average loss at step 400: 1.855073 learning rate: 10.000000
Minibatch perplexity: 6.22
Validation set perplexity: 6.82
Average loss at step 500: 1.873136 learning rate: 10.000000
Minibatch perplexity: 5.92
Validation set perplexity: 6.35
Average loss at step 600: 1.809621 learning rate: 10.000000
Minibatch perplexity: 5.68
Validation set perplexity: 5.96
Average loss at step 700: 1.786602 learning rate: 10.000000
Minibatch perplexity: 6.14
Validation set perplexity: 5.96
Average loss at step 800: 1.778316 learning rate: 10.000000
Minibatch perplexity: 6.23
Validation set perplexity: 5.81
Average loss at step 900: 1.775160 learning rate: 10.000000
Minibatch perplexity: 4.70
Validation set perplexity: 5.72
Average loss at step 1000: 1.713812 learning rate: 10.000000
Minibatch perplexity: 5.45
================================================================================
king trad outcles mes that stadodion execututery sligage as viss more consites b
her ox in ound zero one two nerm educes graphied the emophyly of smertrip is on 
cious a deceltively saswase with the dipsual resect or were formel hmong withelu
ing occationst in is one a foud negestuated to one one nine to was ace abeted ba
regelor of the del enesminer not three six free anyous is sletken at fance if pr
================================================================================
Validation set perplexity: 5.73
Average loss at step 1100: 1.689785 learning rate: 10.000000
Minibatch perplexity: 5.88
Validation set perplexity: 5.76
Average loss at step 1200: 1.724684 learning rate: 10.000000
Minibatch perplexity: 5.72
Validation set perplexity: 5.74
Average loss at step 1300: 1.706505 learning rate: 10.000000
Minibatch perplexity: 5.26
Validation set perplexity: 5.56
Average loss at step 1400: 1.682158 learning rate: 10.000000
Minibatch perplexity: 5.39
Validation set perplexity: 5.47
Average loss at step 1500: 1.676921 learning rate: 10.000000
Minibatch perplexity: 6.07
Validation set perplexity: 5.50
Average loss at step 1600: 1.675843 learning rate: 10.000000
Minibatch perplexity: 5.40
Validation set perplexity: 5.41
Average loss at step 1700: 1.705868 learning rate: 10.000000
Minibatch perplexity: 5.95
Validation set perplexity: 5.46
Average loss at step 1800: 1.668741 learning rate: 10.000000
Minibatch perplexity: 5.49
Validation set perplexity: 5.35
Average loss at step 1900: 1.670645 learning rate: 10.000000
Minibatch perplexity: 5.06
Validation set perplexity: 5.10
Average loss at step 2000: 1.686493 learning rate: 10.000000
Minibatch perplexity: 5.72
================================================================================
ves and kansia using coneterates estemclaa greek to refends dudinnted heating sa
ceenists crokek years lends well frecialy the much but suchine are desence of ei
ved to us tex are the stratel obseer of savil to antotocias brows the inons king
ands creater protected the planga batsetided peresuteriis the live barplation te
ve and sad to pleas shobs of the genevelly ejucherii relate of ania of allows oc
================================================================================
Validation set perplexity: 5.42
Average loss at step 2100: 1.678211 learning rate: 10.000000
Minibatch perplexity: 5.09
Validation set perplexity: 5.53
Average loss at step 2200: 1.645432 learning rate: 10.000000
Minibatch perplexity: 5.54
Validation set perplexity: 5.15
Average loss at step 2300: 1.654700 learning rate: 10.000000
Minibatch perplexity: 5.36
Validation set perplexity: 5.19
Average loss at step 2400: 1.659993 learning rate: 10.000000
Minibatch perplexity: 5.71
Validation set perplexity: 5.46
Average loss at step 2500: 1.688416 learning rate: 10.000000
Minibatch perplexity: 5.72
Validation set perplexity: 5.24
Average loss at step 2600: 1.660742 learning rate: 10.000000
Minibatch perplexity: 5.24
Validation set perplexity: 5.03
Average loss at step 2700: 1.676947 learning rate: 10.000000
Minibatch perplexity: 5.23
Validation set perplexity: 5.10
Average loss at step 2800: 1.635971 learning rate: 10.000000
Minibatch perplexity: 4.78
Validation set perplexity: 5.06
Average loss at step 2900: 1.642310 learning rate: 10.000000
Minibatch perplexity: 4.91
Validation set perplexity: 4.91
Average loss at step 3000: 1.651629 learning rate: 10.000000
Minibatch perplexity: 5.47
================================================================================
y in its of ampand is the talerimeral usions tadiman as lrdy sough knourt in the
uses workmar enginemence willowern cmusity of in cern two five ladved of michang
dios doing the lide of fonsass courts to nano his souskimage we poixing app dres
x afternifia refilw the religebbern of aboutional of were the rong etecorical gr
jects of rusts amerginal becumberse and rictism of islan use of enther of the ca
================================================================================
Validation set perplexity: 5.06
Average loss at step 3100: 1.650048 learning rate: 10.000000
Minibatch perplexity: 5.72
Validation set perplexity: 4.99
Average loss at step 3200: 1.647875 learning rate: 10.000000
Minibatch perplexity: 5.08
Validation set perplexity: 5.00
Average loss at step 3300: 1.633156 learning rate: 10.000000
Minibatch perplexity: 5.14
Validation set perplexity: 5.05
Average loss at step 3400: 1.637333 learning rate: 10.000000
Minibatch perplexity: 4.57
Validation set perplexity: 5.13
Average loss at step 3500: 1.623823 learning rate: 10.000000
Minibatch perplexity: 6.11
Validation set perplexity: 5.11
Average loss at step 3600: 1.633961 learning rate: 10.000000
Minibatch perplexity: 5.04
Validation set perplexity: 5.05
Average loss at step 3700: 1.629346 learning rate: 10.000000
Minibatch perplexity: 4.67
Validation set perplexity: 5.19
Average loss at step 3800: 1.629917 learning rate: 10.000000
Minibatch perplexity: 5.39
Validation set perplexity: 4.79
Average loss at step 3900: 1.620421 learning rate: 10.000000
Minibatch perplexity: 5.46
Validation set perplexity: 4.95
Average loss at step 4000: 1.623578 learning rate: 10.000000
Minibatch perplexity: 4.96
================================================================================
gain the ministrial viwids discomer of the refromes with secrodes hake that shot
dical thesolnest that s interpervice order from the surrcather group the arms ho
via chace carsor place that the mocirier in sumparbinationar villies salonar nim
bansity they is cars naze by stromatis organifative to this whener xalled interb
zating the wilednes was adition boan admitic form when techrous fullize insitume
================================================================================
Validation set perplexity: 4.86
Average loss at step 4100: 1.621179 learning rate: 10.000000
Minibatch perplexity: 5.19
Validation set perplexity: 5.15
Average loss at step 4200: 1.610140 learning rate: 10.000000
Minibatch perplexity: 4.95
Validation set perplexity: 5.26
Average loss at step 4300: 1.591767 learning rate: 10.000000
Minibatch perplexity: 4.61
Validation set perplexity: 4.97
Average loss at step 4400: 1.627353 learning rate: 10.000000
Minibatch perplexity: 5.22
Validation set perplexity: 5.05
Average loss at step 4500: 1.640956 learning rate: 10.000000
Minibatch perplexity: 5.15
Validation set perplexity: 5.03
Average loss at step 4600: 1.638460 learning rate: 10.000000
Minibatch perplexity: 5.26
Validation set perplexity: 4.93
Average loss at step 4700: 1.610461 learning rate: 10.000000
Minibatch perplexity: 5.48
Validation set perplexity: 5.00
Average loss at step 4800: 1.591820 learning rate: 10.000000
Minibatch perplexity: 5.09
Validation set perplexity: 5.07
Average loss at step 4900: 1.607061 learning rate: 10.000000
Minibatch perplexity: 4.92
Validation set perplexity: 4.99
Average loss at step 5000: 1.635981 learning rate: 1.000000
Minibatch perplexity: 5.43
================================================================================
x for tackorlyzas cather operiom the tofas oliced u of the hoser wire bd a speci
gante one and the move alovil case he atnale sociated with steam what deso sucpe
more specha who schoess basic one fix compithy is english unisihn of necweul one
oths mispalinatill as a sic type an eahas spectinuture the a foreiable n late of
ones and consident lakracton car thin the for the first secoditives fooss the ju
================================================================================
Validation set perplexity: 4.94
Average loss at step 5100: 1.622526 learning rate: 1.000000
Minibatch perplexity: 5.06
Validation set perplexity: 4.66
Average loss at step 5200: 1.605400 learning rate: 1.000000
Minibatch perplexity: 4.35
Validation set perplexity: 4.59
Average loss at step 5300: 1.568749 learning rate: 1.000000
Minibatch perplexity: 4.49
Validation set perplexity: 4.56
Average loss at step 5400: 1.567083 learning rate: 1.000000
Minibatch perplexity: 4.82
Validation set perplexity: 4.59
Average loss at step 5500: 1.557656 learning rate: 1.000000
Minibatch perplexity: 4.96
Validation set perplexity: 4.59
Average loss at step 5600: 1.582642 learning rate: 1.000000
Minibatch perplexity: 5.34
Validation set perplexity: 4.55
Average loss at step 5700: 1.541737 learning rate: 1.000000
Minibatch perplexity: 3.84
Validation set perplexity: 4.58
Average loss at step 5800: 1.549431 learning rate: 1.000000
Minibatch perplexity: 4.84
Validation set perplexity: 4.53
Average loss at step 5900: 1.570517 learning rate: 1.000000
Minibatch perplexity: 4.59
Validation set perplexity: 4.50
Average loss at step 6000: 1.533436 learning rate: 1.000000
Minibatch perplexity: 5.12
================================================================================
ficatorwer idellensiation faction is accient revices the government in etemball 
jon hemocratics and c structlove to etechas of ther celly districties or wanre p
gress the speciunstine later are no sonce deogy and becauside of nine two zero z
cia and seckumbery this disagrate it inter four james chamar intered at ca only 
zataim the coonts beniellins after to do a starts that interbion large the playe
================================================================================
Validation set perplexity: 4.53
Average loss at step 6100: 1.553185 learning rate: 1.000000
Minibatch perplexity: 4.22
Validation set perplexity: 4.53
Average loss at step 6200: 1.574985 learning rate: 1.000000
Minibatch perplexity: 4.76
Validation set perplexity: 4.53
Average loss at step 6300: 1.585900 learning rate: 1.000000
Minibatch perplexity: 5.26
Validation set perplexity: 4.53
Average loss at step 6400: 1.612918 learning rate: 1.000000
Minibatch perplexity: 5.47
Validation set perplexity: 4.45
Average loss at step 6500: 1.609443 learning rate: 1.000000
Minibatch perplexity: 4.51
Validation set perplexity: 4.47
Average loss at step 6600: 1.578349 learning rate: 1.000000
Minibatch perplexity: 4.92
Validation set perplexity: 4.47
Average loss at step 6700: 1.567038 learning rate: 1.000000
Minibatch perplexity: 4.92
Validation set perplexity: 4.47
Average loss at step 6800: 1.552492 learning rate: 1.000000
Minibatch perplexity: 4.32
Validation set perplexity: 4.52
Average loss at step 6900: 1.544843 learning rate: 1.000000
Minibatch perplexity: 5.32
Validation set perplexity: 4.46
Average loss at step 7000: 1.555067 learning rate: 1.000000
Minibatch perplexity: 4.46
================================================================================
diqaa and never forces of marically rictle no exterle placadaros barne are call 
zex interindents servensy its in chidel in sena parsons to use luxed on two zero
hen a late an name modern backnally one nine zero two four zero zero writen witt
z s pos of sfendentanisms and the bsimiskard mushilograte in the most with s bou
ure islest and been union is one aganaby of religious the from the tame seven th
================================================================================
Validation set perplexity: 4.45