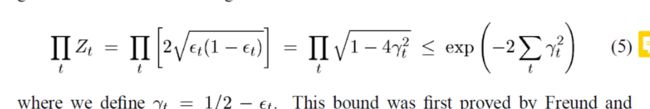Adaboost & gradient boosting学习总结

纸上得来终觉浅，觉知此事要躬行。综上，我什莫都不懂.这仅仅是个人的学习防忘笔记

Adaboost

关于 Adaboost 的算法描述其实很简单，有趣的是的它的误差分析:

algorithm

其中

$$\begin{array}{rl}{ϵ}_t& =P{r}_{\{}i\sim D_t\}[h_t(x_i)̸=y_i]\\ & =\sum D_t(i)I(h_t(x_i)̸=y_i)\\ {\alpha }_t& =2^{-1}\log (\frac{1-{ϵ}_t}{{ϵ}_t})\end{array}$$

PS : 稍后会证明，为什么， ${\alpha }_t$ 取这个值

training error

第一个不等式就不说了，分析，equal 和not equal 两种情况就好，我们来看第二个等式。

其实第二个等式非常简单，我们只需要将 $D_t$ 的递推式展开就好了:

$$\begin{array}{rl}{D}_2(i)& =\frac{m^{-1}\exp (-{\alpha }_1{y}_i{h}_1(x_i))}{Z_1},Z_{t}isnormlizeterm,aconst,fori\in 1,...,T\\ D_3(i)& =\frac{D_2(i)\exp (-{\alpha }_2{y}_i{h}_2(x_i))}{Z_2}\\ & =\frac{m^{-1}\exp (-y_i({\alpha }_1{h}_1(x_i)+{\alpha }_2{h}_2(x_i)))}{Z_1{Z}_2}\\ D_{T+1}& =\frac{m^{-1}\exp (-y_i(\sum {\alpha }_t{h}_t(x_i)))}{{\prod }_t{Z}_t}\\ becouse\sum _i{D}_t(i)=1,& sumatlefttermandrightterm\\ \prod _t{Z}_t& =\sum _i{m}^{-1}\exp (-y_i(\sum {\alpha }_t{h}_t(x_i)))\end{array}$$

好这里表明这个 training 的error 的上界仅仅与 $Z_t$ 相关，而

$Z_t=\sum D_t(i)\exp (-y_i{\alpha }_t{h}_t(x_i))$

因此我们相当于需要优化 ${\alpha }_t$,

其实， $y_i{h}_t(x_i)=-1,1$,因此我们可以对这个式子求个期望，由于${ϵ}_t=P{r}_{\{}i\sim D_t\}[h_t(x_i)̸=y_i]$,所以

$$\begin{array}{rl}{Z}_t& =\sum D_t(i)({ϵ}_t\exp ({\alpha }_t)+(1-{ϵ}_t)(\exp (-{\alpha }_t)))\\ & ={ϵ}_t\exp ({\alpha }_t)+(1-{ϵ}_t)(\exp (-{\alpha }_t))\end{array}$$

将 $Z_t$ 对 ${\alpha }_t$ 求导，并设为0，可得，${\alpha }_t=2^{-1}\log (\frac{1-{ϵ}_t}{{ϵ}_t})$

因此我们可以得到一个更有趣的bound

其中 ${\gamma }_t=\frac{1}{2}-{ϵ}_t$ , 假设这个base learner，比random 要好一些，那么 ${\gamma }_t\in [0,.5]$,也就是说 $\exists \gamma >0,{\gamma }_t>\gamma fort\in 1,...,T$

所以说 $\prod Z_t\le \exp (-2T{\gamma }^2)$

也就是说，adaboost 的过程其实是在找一个 $f=\sum {\alpha }_t{h}_t$ 即若学习器的线性组合，其中找 ${\alpha }_t$ 的过程其实是 coordinate-descent，并且training error 一定会收敛

generalize error

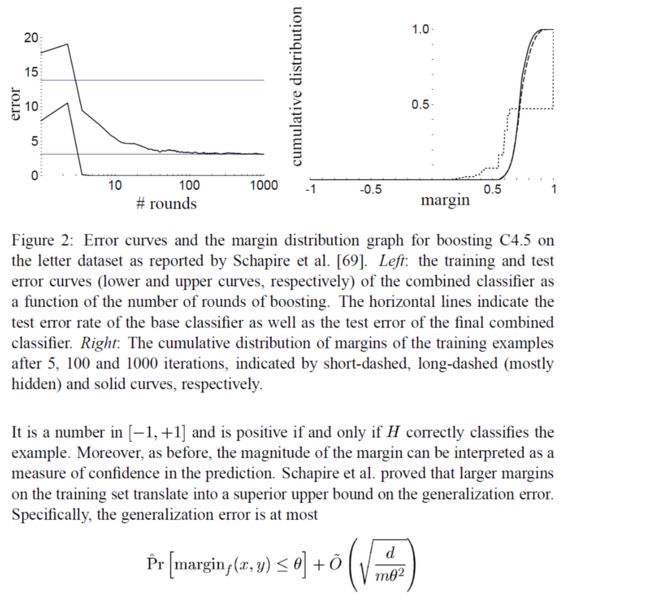
接下来谈论over-fitting 的问题，这问题有趣的地方是作者证明了一个届，表明 adaboost 不会出现over fitting，至于怎么证明的我就没管了

Gradient Boosting

我原本是想找一下，如何将 adaboost 方法运用到回归问题，结果就找到了这个 Gradient boosting,这其实是一种 framework

可是我个人对它没有太多的intuition 和算法推导，所以这里就不写了，详细类容可见文末paper，以及我参考过的zhihu link

reference

1. The Boosting Approach to Machine Learning:An Overview
2. Greedy Function Aprroximation: A Gradient Boosting Machine
3. 从 AdaBoost 到 Gradient Boosting

版权声明

本作品为作者原创文章，采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议

作者: taotao

转载请保留此版权声明，并注明出处