LeetCode总结,动态规划问题小结
一,参考一般书籍中的“动态规划”讲解
1、基本概念
动态规划是一种灵活的方法,不存在一种万能的动态规划算法可以解决各类最优化问题(每种算法都有它的缺陷)。所以除了要对基本概念和方法正确理解外,必须具体问题具体分析处理,用灵活的方法建立数学模型,用创造性的技巧去求解。
2、基本思想与策略
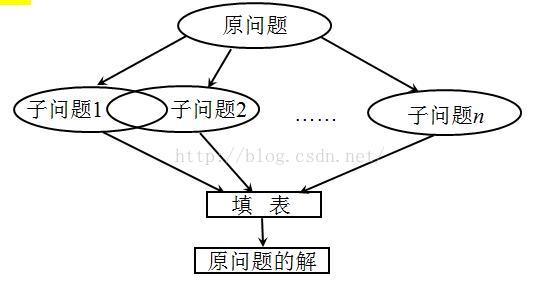
基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
动态规划中的子问题往往不是相互独立的(即子问题重叠)。在求解的过程中,许多子问题的解被反复地使用。为了避免重复计算,动态规划算法采用了填表来保存子问题解的方法。
3、适用的情况
1)两个必备要素
适合应用动态规划方法求解的最优化问题应该具备两个重要的要素:最优子结构和子问题重叠。
(a)最优子结构:问题的最优解由相关子问题的最优解组合而成,并且可以独立求解子问题!
(b)子问题重叠:递归过程反复的在求解相同的子问题。
2)三个性质
能采用动态规划求解的问题的一般要具有3个性质:
(a) 最优化原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
(b) 无后效性:即某阶段状态(定义的新子问题)一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与其以前的状态有关。
(c)有重叠子问题:即子问题之间是不独立的(分治法是独立的),一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
4、求解的基本步骤
实际应用中可以按以下几个简化的步骤进行设计:
(1)分析最优解的性质,并刻画其结构特征,这一步的开始时一定要从子问题入手。
(2)定义最优解变量,定义递归最优解公式。
(3)以自底向上计算出最优值(或自顶向下的记忆化方式(即备忘录法))
(4)根据计算最优值时得到的信息,构造问题的最优解
二,动态规划的自我总结
实际上动态规划的问题就是在牺牲一定量的内存存储子问题的计算结果,从而未来需要这些信息时不再重复计算,直接获取计算过的结果即可。其实动态规划的问题不好想,除非递推公式比较明显。
1,动态规划问题的判断
那么什么样的问题是动态规划呢?
比如如下几个经典问题
这一系列的问题都是最优值问题,能从题目中露骨的感受到求取最优结果的意思。
比如最长回文...最长上升序列...等等。实际上刷题刷多了之后一看就知道是动态规划问题。
2,归纳设计步骤
实际应用中可以按以下几个简化的步骤进行设计:
(1)定义子问题变量,分析递归最优解的公式。
思考问题时一般都是将问题的规模缩小,即较小的子问题,假定其已经获得了最优值,然后将其扩大一点点成为较大规模的子问题,那么较大规模子问题应该怎样从较小规模的子问题递推公式得到呢?并且使得当前的子问题也是最优值。
(2)分析最优解的性质,并刻画其结构特征。
说白了就是刻意寻找定义的子问题变量与前面更小规模子问题变量的关系,一般用一个关系式表达。
(3)以自底向上计算出最优值
所谓自底向上的递推过程,即由较小规模的子问题遍历到原问题。首先我们的原问题是什么?那么他的较小规模的子问题是什么?然后思考我们应该怎么样遍历才能遍历回原问题(首先思考遍历的最外层)。在以后的遍历过程就是通过某种遍历顺序遍历回原问题。比如,最长回文字符串,我们定义的子问题就是“dp[i][j] 表示子串s[i…j]是否是回文”。子串s[i…j]就是原问题的缩小版本,因为我们始终可以通过控制两个变量变回原问题。
(4)实际编写程序时一定要记得初始化
有的边界问题可能不能由递推公式获得。比如最长回文字符串,必须先初始化,这一步一定要纳入思考的范围。
三,分析几个经典的动态规划例子
例子1
最长回文字符串
说真的这个动态规划问题的子问题不好一下想到,为什么不是“dp[i] 表示子串s[0…i]是否是回文”呢?恐怕要经过多番假设子问题才能最终找到正确的子问题设定。
定义子问题:dp[i][j] 表示子串s[i…j]是否是回文,我们这样定义实际上变相知道了当前回文子串的长度,以及在原字符串中的位置。
1,初始化:
1),dp[i][i] = true (0 <= i <= n-1);
2),if(s[i]==s[i+1]), dp[i][i+1] = true (0 <= i <= n-2);
3),其余的初始化为false
2,在初始化基础上的递推过程
如果子问题dp[i+1][j-1] == true,并且扩张一个位置后s[i] == s[j]
显然当前位置,dp[i][j] = true,否则还是为false(意义就是,小的子串都不是回文,在此基础上更大的子串也不是回文)在动态规划中更新最长回文的长度及起点以及长度即可
3,自底向上的遍历
从大的方向上来考虑:动态规划是自底向上的递推过程,即由较小规模的子问题遍历到原问题。
首先我们的原问题是什么?在给定字符串s中寻找最长的回文。
那么他的较小规模的子问题是什么?正如前面别人家的分析所知,我们必须先知道较短长度s.size()-2的子串是否是回文,那么s.size()的源字符串就可以被判断出来
接着唠嗑,为了判断“较短长度s.size()-1的子串是否为回文”,我们必须先知道较短长度s.size()-3的子串是否是回文,那么s.size()-1的源字符串就可以被判断出来
接着唠嗑,为了判断“较短长度s.size()-2的子串是否为回文”,我们必须先知道较短长度s.size()-4的子串是否是回文,那么s.size()-2的源字符串就可以被判断出来
...............
显然循环的最外层就是当前要判断的子串的长度,由小到大。
循环的最内层就是遍历当前指定子串长度的起点和终点,
而最长的回文在我们遍历的过程更新即可!
例子2
跳台阶问题
LeetCode解题报告 70. Climbing Stairs
定义子问题:令vec[i]表示跳到第i步可行的不同方式数目
接着寻找当前子问题vec[i]与前面子问题的关系,
如果是用两步跳过来的(跳到第i步)则vec[i]=vec[i-2],因为这两步已经确定了,那么只有vec[i-2]中可能
如果是用一步跳过来的(跳到第i步)则vec[i]=vec[i-1],因为这一步已经确定了,那么只有vec[i-1]中可能
时间复杂度:O(n)
空间复杂度:O(n)
例子3
经典的股票买卖问题
以下是123题的动态规划分析(同样适用于188题):
本体和背包问题一样,有两个变量,第i天,交易第j次
定义子问题:f[i][j]表示前i天交易j次能得到的最大利润
1,
对于第i天的物品有两种选择情况:交易(买或者卖)或者不做任何交易
1)如果不做任何交易:
显然,此时的最大利润还是前一天的最大利润f[j][i] =f[i-1][j]
2)如果交易:
为了能在这一天获得最大利润如果执行交易显然只能卖股票(不能买),也就是说只能加上当前price[i]:
那么在加上此值price[i]之前的临时利润必须是最大的(可以反正法证明),我们称之为最大临时利润maxtmp,
即如果交易,f[j][i] = prices[i] +maxtmp;
综上两种情况,f[j][i] = max(f[j][i-1], prices[i] +maxtmp);
继续求取maxtmp,
对于最大临时值maxtmp其实也是动态规划过程
显然遍历数组时求出最大,此时只有两种情况:每一次可以买,也可以不买
a)若不买:显然还是以前的maxtmp,即不变
b)若买:为了能最大显然是第j-1次的利润减去,f[i][j - 1] - price[i]
综上两种情况,maxtmp=max(maxtmp,f[i][j - 1] - price[i])
更具体的分析为:
那么假设第j次交易的买进股票是在第z天(实际上在那一天并不重要,我们只是要一个最大的临时值maxtmp即可) ,其中0
那么当我们遍历到第i天,即在每次加上(遍历到)price[i]这个已知值时,先求出price[i]之前的f[z][j-1]-price[z]这个临时利润值maxtmp (必须是最大的,其实就是模拟:用手头已有的利润减去买股票的支出,所剩的还是最大)
综上所诉
f[j][i] = max(f[j][i-1], prices[i] +maxtmp);
maxtmp=max(maxtmp,f[i][j - 1] - price[i]);
例子4
杨辉三角问题
以下是118的分析,同样适用于119.
定义子问题:result[i][j]为三角形i,j位置的值
1,初始化边界:
for(int i=0;i
for(int i=0;i
2,在初始化基础上的递推过程
比较显然从第二行往下递推:很容易看出result[i][j]=result[i-1][j]+result[i-1][j-1];
注:本博文为EbowTang原创,后续可能继续更新本文。如果转载,请务必复制本条信息!
原文地址:http://blog.csdn.net/ebowtang/article/details/50791500
原作者博客:http://blog.csdn.net/ebowtang
本博客LeetCode题解索引:http://blog.csdn.net/ebowtang/article/details/50668895