启发式算法解决八数码（九宫）问题

人工智能课程实验

  背景知识：

估价函数

在对问题的状态空间进行搜索时，为提高搜索效率需要和被解问题的解有关的大量控制性知识作为搜索的辅助性策略。这些控制信息反映在估价函数中。

估价函数的任务就是估计待搜索节点的重要程度，给这些节点排定次序。估价函数可以是任意一种函数，如有的定义它是节点x处于最佳路径的概率上，或是x节点和目标节点之间的距离等等。在此，我们把估价函数f(n)定义为从初始节点经过n节点到达目标节点的最小代价路径的代价估计值，它的一般形式是：

      f(n) = g(n) + h(n)

其中g(n)是从初始节点到节点n的实际代价，g(n)可以根据生成的搜索树实际计算出来；h(n)是从n到目标节点的最佳路径的代价估计，h(n)主要体现了搜索的启发信息。

1)  状态表示的数据结构

struct  Node

{

    stringfather;

    stringid;

    intf,g=0,h;

    intvalue[3][3];

};

value为3X3的九宫格，表示为当前状态，f,g,h分别对应估价函数中的f(n)= g(n) + h(n)，id为当前状态的唯一表示，即九宫格数字的顺序排序，空格用‘0’来表示，则实例中的第一个状态的id即为‘283164705’，father为父状态的id。

2)  状态扩展规则的表示

从某一状态出发，寻找空格的位置，探寻空格的上下左右四个方向可移动性，并避免走回头路，计算下一节点的估价函数值。

int calcuH(int *value)

{

    int h=0;

    for(int i= 0; i < 9; i++)

    {

        intnum=value[i]-1;

       if(num==-1)continue;

        intnowx=i%3,nowy=i/3;

        intgoalx=num%3,goaly=num/3;

       h+=abs(nowx-goalx)+abs(nowy-goaly);   

    }

    returnh;}

估价函数为所有数字当前的位置和目标位置的水平距离和垂直距离的绝对值的和。

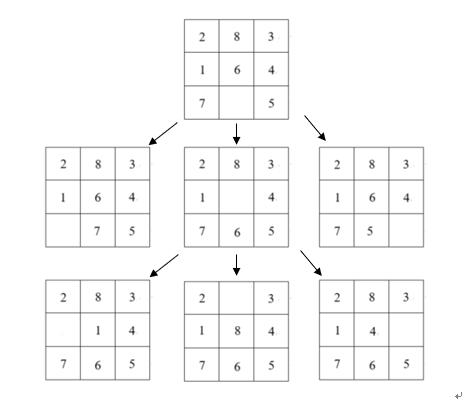
3)  搜索产生的状态空间图

4)  OPEN表和CLOSE表变化过程

从open表取出最后一个状态，进行状态搜索，将新搜索到的点加入open表，后将该状态加入close表，最后重新排序open表。

#include "iostream"
#include 
#include 
#include 
#include 
#include 

using namespace std;

struct  Node
{
    string father;
    string id;
    int f,g=0,h;
    int value[3][3];
};
string getID(int *value)
{
    stringstream ss;
    for(int i = 0; i < 9; i++)
    {
        ss<j.h); }  
vector close;
vector open;
static int oldH=999999;
Node bestResult;
int moveMat[9][4]={
    {0,1,1,0},
    {0,1,1,1},
    {0,0,1,1},
    {1,1,1,0},
    {1,1,1,1},
    {1,0,1,1},
    {1,1,0,0},
    {1,1,0,1},
    {1,0,0,1}
};//move mat ,list as up right down left

void outPrint( Node result )
{
    vector::iterator iter;
    stack outStack;
    outStack.push(result);
    int time=-1;
    while(result.father!="start")
    {
        result.id=result.father;
        iter = find(close.begin(), close.end(), result);
        if(iter != close.end())
        {
            result=*iter;
            outStack.push(result);
        }
        else
        {
            cout<<"program error in outprint"< ";
                    else
                        cout<<"    ";                    
                }
                cout< ";
            else
                cout<<"    ";                    
        }
        cout<::iterator iter;
        iter = find(close.begin(), close.end(), node);
        if(iter != close.end())
        {
            if(iter->g>node.g)
            {
                iter->father=node.father;
                iter->g=node.g;
                iter->f=node.f;
            }           
        }
        else 
        {
            iter = find(open.begin(), open.end(), node);
            if(iter != open.end())
            {
                if(iter->g>node.g)
                {
                    iter->father=node.father;
                    iter->g=node.g;
                    iter->f=node.f;
                }    
            }
            else                         //if not in close or open ,add new
            {
                open.push_back(node);
            }
        }
    }

}

int search()
{
    int loop=0;
    int staytime=0;
    while(!open.empty())
   {
        
        sort(open.begin(),open.end(),cmpH);

        Node nowNode=open.back();
        int *pvalue=(int*)nowNode.value;
        {
            if(nowNode.hstart[j])
            {
                inversion++;
            }   
        }       
    }
    //cout<