cs224n学习笔记 01: Introduction and word vectors

关键词: Word Vectors, SVD (Singular Value Decomposition), Skip-gram, Continuous Bag of Words (CBOW), Negative Sampling, Hierarchical softmax, Word2Vec.

本节首先介绍NLP的一些一本概念和常见的NLP问题；然后讨论如何用向量（numeric vector）来表示一个一个的单词（word）；最后，我们对时下比较流行生成word vector方法进行探讨。

目录

目录

1. Introduction to NLP

1.1 常见的NLP任务

1.2 How to represent words？

2. Word Vectors词向量

3. one-hot vector

4 SVD based methods

4.1 如何生成矩阵X?

4.1.1 Word-Document Matrix

4.1.2 Window-based Co-occurrence Matrix

4.2 SVD

4.2.3 SVD-based methods的缺点和现有的解决方案

5 Iteration-based methods - Word2vec

5.1 Language Models 语言模型

5.2 Continuous Bag of Words Model (CBOW) 

5.3 Skim-gram Model

5.4 Negative samping

5.5 Hierarchical softmax

5.5.1 与CBOW和Skim-gram的结合

6. References 

---

1. Introduction to NLP

1.1 常见的NLP任务

• 简单的task:  Spell Checking 拼写检查；Keyword Search 关键词搜索；Finding Synonyms 同义词查找
• 中等难度的task：解析来自网站、文档的信息
• 较高难度的task：Machine translation 机器翻译（中英互译）；Semantic Analysis 语义分析（查询语句的含义）；Coreference 指代消除 （文档中的“it”或者“he”指代什么）；Question Answering 问答系统 

1.2 How to represent words？

所有的NLP任务中，首要并且最重要的就是如何表示输入的单词？答案就是：Represent Words as Word Vectors. 使用用词向量来表示单词，这样就可以比较容易的衡量词与词之间的相似性与差异性。例如，使用cosine similarity、欧式距离等衡量词的相似性。

2. Word Vectors词向量

英语中近130万的单词，并且这些单词之间也存在一定的联系，比如：cat-feline，hotel-motel。很多研究表明，可以只要使用N维的向量空间，其中万，就足以对一种语言的全部语义进行表达。例如，语义空间可以表示出时态（过去时、现在时、奇偶、性别等信息。

常用的生成word vectors方法可以分为以下几类：

• one-hot vector
• SVD-based methods
• Iterations-based methods - word2vec

接下来，我们会对这些种类的方法进行详细介绍。注意，word vectors也可以写成word embeddings.

3. one-hot vector

one-hot vector方法是最简单和直接的一种。设语料库包括个不同的单词，对单词进行排序，用维的向量来表示每一个单词，向量只由0和1组成，其中该单词的对应的位置的值为1。具体例子如下：

可以看出，one-hot vector方法生成的word vectors，单词与单词之间是完全独立的。其缺点是反映不出词之间的相关性，例如：

因此，我们可以尝试降低向量空间的维度，寻找其他子空间对词与词之间的联系进行编码。

4 SVD based methods

SVD-based methods方法的通用流程：

• 遍历数据集并基于某些规则生成矩阵X，
• 然后使用Singular Value Decomposition（SVD奇异值分解）将X分解成。其中U的每一行就是对应单词的向量表示。

4.1 如何生成矩阵X?

本小节介绍两种生成矩阵X的方法，分别为Word-Document Matrix和Window-based co-occurrence Matrix。

4.1.1 Word-Document Matrix

“相关的词汇会经常出现在相同的文档中”，这个假设是很make sense的。例如：“银行”、“股票”、“钱”就会经常一起出现在同一篇文章中。因此基于这个假设，我们可以构建word-document Matrix，计算过程如下：

输入：个文档，这些文档由个不同的单词组成 输出: 矩阵，其中 ，代表单词出现在文档中的次数 过程：       For document_j in documents:             IF word_i appears in document_j:             THEN               END IF       END FOR

可以看出，X是一个相当大的矩阵。有没有其他更好的办法呢？

4.1.2 Window-based Co-occurrence Matrix

用矩阵X存储co-occurrence words（一起出现的词）之间的关系。其中，设语料库中共包括个不同的单词，X的维度为，表示单词出现在单词的给定大小的邻域中的次数。

邻域的定义：设window-size=1，那么给定单词的左右相邻的各1个单词就是它的co-occurrence words，例如：

I like the sun，当window-size为1时，被"the"的co-occurrence words为"like"和”sun“。

Window-based co-occurrence Matrix计算过程举例：

 

设语料库只包括3个句子，分别为： 1. I enjoy flying. 2. I like NLP. 3. I like deep learning   设窗口大小window-size=1，那么对应的输出结果应该为： 例如，deep出现在like邻域窗口的次数为1，故而矩阵中对应的值为1。

4.2 SVD

计算出矩阵X之后，就可以使用SVD对X进行分解，得到。

如下图所示，。

其中S是对角矩阵，对角线的值代表奇异值singular values，已经按照值的大小倒序排列。

用选取U的前k列，U的每一行表示SVD降维后的对应单词的word vector。这样，每个单词就可以用k维向量表示。

使用下面的公式可以计算出使用这k个维度作为降维结果能够保留的信息比例。

4.2.3 SVD-based methods的缺点和现有的解决方案

• 优点：
  • 上述基于计数的来构建矩阵的方式能够更好的利用global的统计信息
• 缺点：
  • 矩阵的维度会经常改变。每当出现一个新的词或语料库中词的数量发生改变时，就需要调整矩阵的维度
  • 由于存在大量的词之间不存在co-occurrence的关系，因此矩阵会非常稀疏
  • 矩阵的维度会非常高，通常会近似为
  • SVD计算量非常大
  • 需要额外处理词频分布不均的问题
• 现有的解决方案
  • 去除function words,如：the，a，he，her....
  • 使用改进的window，例如：加权窗口
  • 使用皮尔逊相关并设置负计数，而不是只使用原始计数

5 Iteration-based methods - Word2vec

在介绍iteration-based methods之前，我们先简单介绍一下word2vec。

Word2vec是一个software package，它由以下两部分组成构成：

• 2种生成word vectors的算法：skim-gram和continuous bag-of-words (CBOW)。
• 2种训练方式：Negative sampling和Hierarchical softmax。这两种训练方式是为了减少使用CBOW或skim-gram来生成词向量的训练过程的计算量。

目前大家只要知道word2vec就是一个软件包，里面包括2个生成词向量的算法分别是skim-gram和continuous bag-of-words (CBOW)，以及2种减少训练过程计算量的训练方法。接下来，我们会对Word2vec的各个部分进行详细介绍。

现在，让我们正式进入本节的内容。

与第4节介绍的基于方法不同，Iteration-based methods不采用基于全部数据集的统计信息，而是基于局部的上下文信息（context ）来创建一个模型，这个模型能够通过迭代的方式不断更新待学习的参数——word vectors。为了能够让模型学习到最终的word vectors，我们需要定义损失函数来衡量每一步迭代的errors，然后根据error的变化来更新参数，例如可以通过梯度下降法对参数进行更新。word2vec就包含了两种常用的iteration-based methods。

context of words的定义：就是给定单词x，围绕与x左右相邻的、距离在小于等于m的词。以window-size=2为例，在句子”The quick brown fox jumped over the lazy dog“中，fox的context就是{"quick","brown","jumped","over"}。

5.1 Language Models 语言模型

首先，我们创建一个模型来表示由默写单词组成的句子出现的概率。以下面的句子为例：

                               “The cat jumped over the puddle”

一个好的语言模型能够给出这个句子出现的可能性，包括：语义上和语法上出现的可能性。可以看出，上面的句子出现的可能性很大。而“stock boil fish is toy”出现的可能性会很低，因为make no sense。

由n个单词组成的句子出现的概率可以的数学方式进行描述，公式如下：

假设句子中的每个单词都是独立的，那么模型可以被表示为：

但是我们知道，句子中的单词不肯能独立，它们之间一定存在依赖关系。因此，我们可以增强一下假设，令句子中的每个单子只依赖于其前面的一个词，这样的话模型可以表示为：

当然，我们知道这个假设也是非常的naive的，该假设只考虑了单词的context上下文信息，而没有从句子的整体进行考虑。但是这个假设也足以帮助我们做很多事，例如：在基于window-size=1生成的Word-Word Matrix中，就可以给出两个词同时出现的概率；但是，我们知道在这种情况下它的计算量很大。

接下来，我们就要开始介绍word2vec中的两个algorithms和两个training models。

5.2 Continuous Bag of Words Model (CBOW) 

首先再次强调一下，CBOW是一种基于迭代的、学习word vectors的方法。

它的思想是：给定一个中心词的上下文单词，预测这个中心词是是什么。例如：{"the","cat","?", "over","the","puuddle"}，预测“?”是哪个词。

因此，CBOW训练数据由（中心词对应的context，中心词）组成，其中中心词就是数据的label。

接下来我们开始介绍CBOW的具体实现：

• 首先，我们给出一些已知参数的定义：

  • 设数据集共包括个不同的单词

  • 首先为数据集生成one-hot编码的word vectors，然后用词向量的组合来表示数据集中的每一个句子

  • ：代表句子中第c个单词对应的one-hot word vector，；

  • ：表示模型对该组输入数据做出的中心词的预测结果，；

  • ：代表该组数据的label，就是这个真实中心词对应的one-hot word vector，。

• 接下来，给出需要学些的未知参数的定义。

  • 假设我们希望用维的向量来表示每个单词，就是词向量空间的大小为

  • 创建两个矩阵，分别为：，

    • 代表input word vector，其中每一列为对应单词在作为context word输入时的向量表示

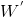    • 代表output word vector，其中每一行代表对应单词作为context word输出时的向量表示

CBOW需要为每个单词学习两个向量，分别为：

• w： input vector，用来表示该单词作为context word输入时的向量表示
• w':   output vector，用来表示该单词作为center word输出时的向量表示

具体步骤如下：

Step 1. 生成one-hot word vectors，其中表示单词c对应的one-hot向量， Step 2. 设上下文窗口大小为m，那么中心词c的上下文就可以被表示为：  Step 3. 计算context的embedded word vectors：，每一个就代表该单词作为context word时的向量表示。 Step 4. 计算，这就是右图中的隐藏层的值 Step 5. 计算score vector：，其中 Step 6. 使用softmax函数将score vector转成概率vector：，其中输出的需要与真实的label 进行比较，其中是真实中心词的one-hot vector

接下来，我们给出CBOW模型的损失函数。对于给定的一组数据，使用cross entropy来度量输出的与真实的label 之间的差别：

由于真实label是一个one-hot vector，只有center word对于的位置才是1，其它位置均为0。因此设第i个单词为真正的中心词，则可以将上面的损失函数可以化简为：

因此，CBOW的目标函数应该为：

这样，就可以使用梯度下降算法来迭代的更新所有的参数。

5.3 Skim-gram Model

再次强调一下， Skim-gram Model是Wordvec中包含的另外一种基于迭代的、学习word vectors的方法。

它的思想是：给定一个中心词，预测这个中心词的上下文单词分别是什么。例如：给定”jump“，预测和生成其周围的context words："the","cat","over","the","puuddle".

因此， Skim-gram Model训练数据由（中心词, 中心词周围的context words）组成，其中中心词周围的context words就是数据的label。其实就是将CBOW中的label和数据互换。

接下来我们开始介绍Skim-gram的具体实现：

Skim-gram中的已知参数和未知参数的定义与CBOW完全一样，它的目标也与CBOW完全一样，就是学习和这两个输入向量矩阵和输出向量矩阵，即：为每个单词学到两个向量：

• w： input vector，用来表示该单词作为context word输入时的向量表示
• w':   output vector，用来表示该单词作为center word输出时的向量表示

具体步骤如下：

Step 1. 生成one-hot word vectors，其中表示中心词c对应的one-hot向量， Step 2. 计算中心词对应的embedded word vectors：，就代表该单词作为中心词时的向量表示，这也是右图中隐藏层的输出 Step3. 计算score vector: 。注意，这代表context words中的一个单词的预测得分 Step 4. 将score vector转成概率：。注意。如果context window size=c，那么对于中心词c，就有C=2c个向量输出，分别为：，这就是右图中的输出层的值。       其中输出的需要与真实的label 进行比较，其中是真实context words对应的one-hot vector

与CBOW一样，我们也需要定义目标函数用来评估模型。与CBOW不一样的是，我们引入Naive Bayes假设来简化概率表达式，即：假设所有的context words之间完全独立，就是说Skim-gram的输出词全部完全独立。这样，当只计算一个中心词的context words时，目标函数可以表示为：

--->Naive bayers假设

注意，上面的式子中，第三步可以表示为下面的公式，其中H代表概率的交叉熵。

5.4 Negative samping

回顾一下上面Skim-gram和CBOW的目标函数，可以看到，求和的复杂度非常巨大：。每一次更新都要涉及到的计算量，那么如果需要进行百万级别的更新，那么计算量将会更大。因此，很自然的，我们想通过一些方法来求它的近似值，进而降低计算量。

首先给出Negative example的定义：以Skim-gram为例，一个中心词+context word组成的元组就是一个样本，对于这个样本来说，它的标签应该是一个one-hot向量，并且该向量只有context word c对应的位置的值为1，其余位置的值应该都为0，那么其余任意位置对应的单词与中心词w组成的元组就是一个负样本。

Negative Sampling的思想就是：对于每次迭代，我们不对单词集的全部单词进行遍历，而是从中采样出一些Negative examples(负样本)，仅对这些负样本对应的参数进行更新。采样服从分布，单词被采为负样本的概率与其在语料库中出现的频率大小相关。

当采用negative sampling时，只需要对原始算法的目标函数作以下修改即可：

• 目标函数

MIKOLOV等人提出的Negative Sampling是基于Skim-gram进行改进的。

设表示一个中心词和context word的元组。定义代表属于语料库的概率，这就是正样本的概率；表示不属于语料库的概率，即：负样本的概率。

首先，我们用sigmoid function来对进行建模：

     

然后，我们的目标函数应该是：尽可能的使得确实属于自语料库的中心词+context word对应的最大；并且尽可能的使得确实不属于语料库的元组的概率和最大。则可以表示为：

   

   

   

   

等价于，求其取负后的最小值对应的参数，取负后的损失函数为：

其中，代表属于语料库的集合；代表Negative samples，即没有在语料库中出现的数据，换句话说语料库中没有出现c作为w的上下文单词出现的情况。可以通过随机采样来生成。

对于Skim-gram来说，如果我们计算给定中心词w的第w-m+j的context word，那么目标函数可以写成：

        

对于CBOW来说，给定中心词w的context向量为：，那么目标函数为：

       

注意，

在Skim-gram中代表单词w作为中心词时的向量；代表单词w作为context word时的向量；

而在CBOW中代表单词w作为context word时的向量；代表单词w作为center word时的向量。

• 采样的规则

上文讲到了对负样本进行随机采样，那么接下来就讲一下如何对负样本进行随机采样。

设样本采样的概率服从分布，那么该怎么定义呢？

           一个单词被选作 negative sample 的概率跟它出现的频次有关，出现频次越高的单词越容易被选作negative samples，Word2vec代码中一个单词被选为negative sample的概率的计算公式为：

           

其中，f(w) 代表 每个单词被赋予的一个权重，即：该单词出现的词频；分母代表所有单词的权重和。公式中3/4完全是基于经验的，论文中提到这个公式的效果要比其它公式更加出色。

 

5.5 Hierarchical softmax

在Hierarchical Softmax中，使用霍夫曼编码后的二叉树来表示全部的单词。其中:

• 每个叶子节点代表一个单词，共有个叶子节点，从根节点到每个单词有一条特定的路径。二叉树的输入是一个词向量，输出是叶子节点代表的单词。
• 每个非叶子节点都相当于一个二分类器，决定输入一个词向量之后，决定是采用左子节点还是右子节点包括在路径中直至抵达最后的叶子节点；它涉及到的参数是一个向量，这个向量就是模型需要学习的参数。

给定词向量时，代表单词的概率就等于：从根节点随机游走到对应叶子节点的概率。使用这种方式计算概率，计算cost只要，即：二叉树路径的长度。

该模型的目的不是为了每个单词学得一个词向量，而是要为每个非叶子节点学得其参数向量。

接下来给出一些基本定义：

• ：从根节点到叶子节点的路径上包括的节点的数量。例如下图中，，即：根节点到叶子节点共有3个非叶子结点。
• ：代表从根节点到叶子节点的路径上第个节点
• ：代表从根节点到叶子节点的路径上第个节点对应的向量
• ：代表从根节点输入的向量

因此，代表根节点，代表叶子节点的父节点。

设代表节点的左节点，那么给定词向量时，代表单词的概率为：

where， and

其中，代表：在给定输入向量时，走向单词的路径中第j+1个节点是否为上一个节点的左节点，如果是左节点，则为1，否则为-1。注意sigmoid的函数的特性有：，即：，满足左右节点的概率和为1。另外，。

最后，我们可以通过点乘来计算给定输入向量和每个inner node之间的相似性，再使用sigmoid函数求出路径中每个节点的下一个节点是其左节点还是右节点的概率。例如：上图中的叶子节点,从根节点到它的路径为：根节点-左节点-左节点-右节点，因此：

为了训练模型，我们的目标就是最小化负的log likelihood函数：，然后对里面每个inner node的对应的向量和输入向量进行更新。

5.5.1 与CBOW和Skim-gram的结合

用构建好的霍夫曼树替换CBOW和SKim-gram中的softmax输出层，减少计算量。

• CBOW

1. 输入层：中心词C的context words对应的向量 2. 隐藏层 3. 输出层：霍夫曼树

• Skim-gram

1. 输入层：中心词C+其context words组成的词组 2. 隐藏层 3. 输出层：霍夫曼树

 

6. References 

•  [Bengio et al., 2003] Bengio, Y., Ducharme, R., Vincent, P., and Janvin, C. (2003). A neural probabilistic language model. J. Mach. Learn. Res., 3:1137–1155.
•  [Collobert et al., 2011] Collobert, R., Weston, J., Bottou, L., Karlen, M., Kavukcuoglu, K., and Kuksa, P. P. (2011). Natural language processing (almost) from scratch. CoRR, abs/1103.0398.
•  [Mikolov et al., 2013] Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013). Efficient estimation of word representations in vector space. CoRR, abs/1301.3781.
•  [Rong, 2014] Rong, X. (2014). word2vec parameter learning explained. CoRR, abs/1411.2738.
•  [Rumelhart et al., 1988] Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1988). Neurocomputing: Foundations of research. chapter Learning Representations by Back-propagating Errors, pages 696–699. MIT Press, Cambridge, MA, USA.